Whenever you write a program, you want this program to behave correctly and do what you want it to do. Thus, programming always goes together with the mental act of proving to yourself (and sometimes to other people as well), that the code you write is correct. Most often this "proof" is implicit, dissolved in the way you write your code and comment it. In fact, in my personal opinion, "good code" is exactly the one, where a human-reviewer is able to verify its correctness without too much effort.
It is natural to use computers to help us verify correctness. Everyone who has ever programmed in a strictly-typed programming language, such as Java or Haskell, is familiar with the need to specify types of variables and functions and follow strict rules of type-safety. But of course, ensuring type-safety is just the compiler's way to help you ensure some basic claims about the program, such as "this variable will always contain an integer" or "this function will always be invoked with exactly three parameters".
This is very convenient, yet can be somewhat limiting or annoying at times. After all, type-safety requires you to write code that "can be type-checked". Although very often this is expected of "good code" anyway, there are situations where you would like some more flexibility. For this reason some languages impose no type-safety rules at all (e.g. Python or Javascript), and some languages let you disable type-checking for parts of code.
Rather than disabling the type checker, another principled way to allow more flexibility is to make the type-checker smarter. This is the promise of dependent types. In principle, a language, which supports dependent types, would let you make much more detailed statements about your program and have your program automatically checked for correctness with respect to those statements. Rather than being limited to primitive claims like "this variable is an integer", the use of dependent types enables you to assert things like "this is a sorted list", or "this is an odd integer", and so on up to nearly arbitrary level of detail, in the form of a type annotation. At least that much I found out during a course at the recent winter school.
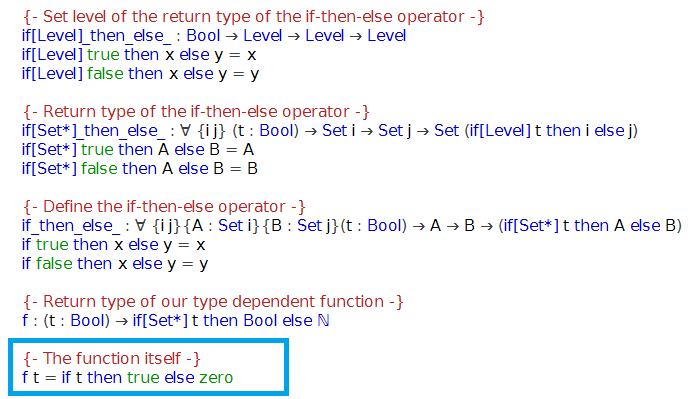
The course was based on the Agda programming language, and the first thing I decided to try implementing in Agda is a well-typed version of the following simple function:
f t = if t then true else 0
It might look like something trivial, yet most traditional strictly typed languages would not let you write this. After all, a function has to have a return type, and it has to be either a Boolean or an Integer, but not both. In this case, however, we expect our function to have a parameter-dependent type:
f : (t : Bool) → if t then Bool else Integer
Given that Agda is designed to support dependent types, how complicated could it be to implement such a simple function? It turns out, it takes a beginner more than an hour of thinking and a couple of consultations with the specialists in the field. The resulting code will include at least three different definitions of "if-then-else" statements and, I must admit, some aspects of it are still not completely clear to me.
This is the longest code I've ever had to write to specify a simple if-then-else statement. The point of this blog post is to share the amusement and suggest you to check out Agda if you are in the mood for some puzzle-solving.
As for dependent types, I guess those are not becoming mainstream any time soon.