Four Years Remaining

A long time ago, information was stored and transmitted by people who passed it in the form of poems from mouth to mouth, generation to generation, until, at some moment, writing was invented. Some poems were lucky enough to be carefully written down in letters on the scrolls of papyrus or pergament, yet a considerable number of them was left unwritten and thus lost. Because in the age of writing, an unwritten poem is a non-existent poem. Later on came the printing press and brought a similar revolution: some books from the past were diligently reprinted in thousands of copies and thus preserved for the future. The remaining ones were effectively lost, because in the age of the printing press, an unpublished book is a nonexistent book. And then came the Internet. Once again, although a lot of the past knowledge has migrated here, a large amount hasn't, which means that is has been lost for most practical purposes. Because in the age of the Internet, if it is not in the Internet, it does not exist. The tendency is especially notable in science, because science is essentially about accumulating knowledge.

The effect of such regular "cleanups" (and I am sure these will continue regularly for as long as humankind exists) is twofold. On one hand, the existing knowledge is reviewed and only the worthy pieces get a chance to be converted into the new media format. As a result, a lot of useless crap is thrown away in an act of natural selection. On the other hand, a considerable amount of valuable information gets lost too, simply because it seemed useless at that specific moment. Of course, it will be reinvented sooner or later anyway, but the fact that it was right here and we just lost it seems disturbing, doesn't it.

I'm still browsing through that old textbook from the previous post and enjoying the somewhat unfamiliar way the material is presented. Bayesian learning, boolean logic and context-free-grammars are collected together and related to decision theory. If I did not know the publication date of the book, I could easily mistake this "old" way of presenting the topic, for being something new. Moreover, I guess that, with an addition of a minor twist, some ideas from the book could probably be republished in a low-impact journal and thus recognized as "novel". It would be close to impossible to figure out the copy, because a pre-Internet-era non-English text simply does not exist.

The day before I've accidentally stumbled upon an old textbook on pattern analysis written in Russian (the second edition of a book originally published in 1977, which is more-or-less the time of the classics). A brief review of its contents was enormously enlightening.

It was both fun and sad to see how smallishly incremental the progress in pattern analysis has been for the last 30 years. If I wasn't told that the book was first published in 1977, I wouldn't be able to tell it from any contemporary textbook. I'm not complaining that the general approaches and techniques haven't changed much, these shouldn't have. What disturbs me is that the vision of the future 30 years ago was not significantly different from what we have today.

Pattern recognition systems nowadays are getting more and more widespread and it is difficult to name a scientific field or an area of industry where these are not used or won't be used in the nearest future...

Further on the text briefly describes the application areas for pattern analysis that range from medicine to agriculture to "intellectual fifth-generation computing machines" and robots that were supposed to be here somewhere around nineties already. And although machines did get somewhat more intelligent, we have clearly failed our past expectations. Our current vision of the future is not significantly different from the one we had 30 years ago. It has probably become somewhat more modest, in fact.

Interesing, is this situation specific to pattern analysis or is it like that in most areas of computer science?

It is somewhat sad to see that the Scalable Vector Graphics (SVG) format, despite its considerable age and maturity, has not yet gained too much popularity in the internet, with a lot of Adobe Flash all over instead. Here are some points you should know about it, so that maybe you consider taking a couple of hours to get acquainted with it one day.

1. SVG is an open source vector graphics format.
2. SVG supports most of what you'd expect from a 2D graphics language: cubic splines, bezier curves, gradients, nested matrix transformations, reusable symbols, etc.
3. SVG is XML-based and rather straightforward. If you need a picture with a line and two circles, you write a <line> tag and two <circle> tags:
   

   <svg xmlns="http://www.w3.org/2000/svg"> <line x1="0" y1="0" x2="100" y2="100" stroke-width="2" stroke="black"/> <circle cx="0" cy="0" r="50"/> <circle cx="100" cy="100" r="20" fill="red" stroke="black"/> </svg>

4. Most vector graphics editors can write SVG. For example, Inkscape is one rather usable open-source software piece.
5. SVG supports Javascript. Basically, if you know HTML and Javascript, you are ready to write SVG by hand, because SVG is also just XML + Javascript. This provides considerable freedom of expression.
   
6. SVG can be conveniently embedded into HTML webpages and is supported out-of-the-box by most modern browsers.

My personal interest towards SVG is related to the observation, that it seems very suitable for creating interactive data visualizations (charts, plots, graphs) right in the browser. And although the existing codebase devoted to these tasks can't be called just enormous, I'm sure it will grow and gain wider adoption. Don't miss it!

Logic versus Statistics

Consider the two algorithms presented below.

Algorithm 1:

   If, for a given brick B,
      B.width(cm) * B.height(cm) * B.length(cm) > 1000
   Then the brick is heavy

Algorithm 2:

   If, for a given male person P,
      P.age(years) + P.weight(kg) * 4 - P.height(cm) * 2 > 100
   Then the person might have health problems

Note that the two algorithms are quite similar, at least from the point of view of the machine executing them: in both cases a decision is produced by performing some simple mathematical operations with a given object. The algorithms are also similar in their behaviour: both work well on average, but can make mistakes from time to time, when given an unusual person, or a rare hollow brick. However, there is one crucial difference between them from the point of view of a human: it is much easier to explain how the algorithm "works'' in the first case, than it is in the second one. And this is what in general distinguishes traditional "logical" algorithms from the machine learning-based approaches.

Of course, explanation is a subjective notion: something, which looks like a reasonable explanation to one person, might seem incomprehensible or insufficient to another one. In general, however, any proper explanation is always a logical reduction of a complex statement to a set of "axioms". An "axiom" here means any "obvious" fact that requires no further explanations. Depending on the subjective simplicity of the axioms and the obviousness of the logical steps, the explanation can be judged as being good or bad, easy or difficult, true or false.

Here is, for example, an explanation of Algorithm 1, that would hopefully satisfy most readers:

• The volume of a rectangular object can be computed as its width*height*length. (axiom, i.e. no further explanation needed)
• A brick is a rectangular object. (axiom)
• Thus, the volume of a brick can be computed as its width*height*length. (logical step)
• The mass of a brick is its volume times the density. (axiom)
• We consider the density of a brick to be at least 1g/cm³ and we consider a brick heavy if it weighs at least 1 kg. (axiom)
• Thus a brick is heavy if its mass > width*height*length > 1000. (logical step, end of explanation)

If you try to deduce a similar explanation for Algorithm 2 you will probably stumble into problems: there are no nice and easy "axioms" to start with, unless, at least, you are really deep into modeling body fat and can assign a meaning to the sum of a person's age with his weight. Things become even murkier if you consider a typical linear classification algorithm used in OCR systems for deciding whether a given picture contains the handwritten letter A or not. The algorithm in its most simple form might look as follows:

   If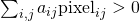 
   Then there is a letter A on the picture,

where 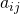are some real numbers that were obtained using an obscure statistical procedure from an obscure dataset of pre-labeled pictures. There is really no good way to explain why the values of 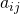are what they are and how this algorithm gets the result, other than to present the dataset of pictures it was trained upon and state that "well, these are all pictures of the letter A, therefore our algorithm detects the letter A on pictures".

Note that, in a sense, such an "explanation" uses each picture of the letter A from the training set as an axiom. However, these axioms are not the kind of statements we used to justify Algorithm 1. The evidence they provide is way too weak for traditional logical inferences. Indeed, the fact that one known image has a letter A on it does not help much in proving that some other given image has an A too. Yet, as there are many of these "weak axioms", one statistical inference step can combine them into a well-performing algorithm. Notice how different this step is from the traditional logical steps, which typically derive each "strong" fact from a small number of other "strong" facts.

So to summarize again: there are two kinds of algorithms, logical and statistical.
The former ones are derived from a few strong facts and can be logically explained. Very often you can find the exact specifications of such algorithms in the internet. The latter ones are based on a large number of "weak facts" and rely on induction rather than logical (i.e. deductive) explanation. Their exact specification (e.g. the actual values for the parameters 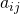used in that OCR classifier) does not make as much general sense as the description of classical algorithms. Instead, you would typically find general principles for constructing such algorithms.

The Human Aspect

What I find interesting, is that the mentioned dichotomy stems more from human psychology than mathematics. After all, the "small" logical steps as well as the "big" statistical inference steps are all just "steps" from the point of view of maths and computation. The crucial difference is mainly due to a human aspect. The logical algorithms, as well as all of the logical decisions we make in our life, is what we often call "reason" or "intelligence". We make decisions based on reasoning many times a day, and we could easily explain the small logical steps behind each of them. But even more often do we make the kind of reason-free decisions that we call "intuitive". Take, for example, visual perception and body control. We do these things by analogy with our previous experiences and cannot really explain the exact algorithm. Professional intuition is another nice example. Suppose a skilled project manager says "I have doubts about this project because I've seen a lot of similar projects and all of them failed". Can he justify his claim? No, no matter how many examples of "similar projects" he presents, none of them will be considered as reasonable evidence from the logical point of view. Is his decision valid? Most probably yes.

Thus, the aforementioned classes of logical (deductive) and statistical (inductive) algorithms seem to directly correspond to reason and intuition in the human mind. But why do we, as humans, tend to consider intuition to be inexplicable and thus make "less sense" than reason? Note that the formal difference between the two classes of algorithms is that in the former case the number of axioms is small and the logical steps are "easy". We are therefore capable of representing the separate axioms and the small logical steps in our minds somehow. However, when the number of axioms is virtually unlimited and the statistical step for combining them is way more complicated, we seem to have no convenient way of tracking them consciously due to our limited brain capacity. This is somewhat analogous to how we can "really understand" why 1+1=2, but will have difficulties trying to grasp the meaning of 121*121=14641. Instead, the corresponding inductive computations can be "wired in" to the lower, unconscious level of our neural tissue by learning patterns from experience.

The Consequences

There was a time at the dawn of computer science, when much hope was put in the area of Artificial Intelligence. There, people attempted to devise "intelligent" algorithms based on formal logic and proofs. The promise was that in a number of years the methods of formal logic would develop to such heights, that would allow computer algorithms to attain "human" level of intelligence. That is, they would be able to walk like humans, talk like humans and do a lot of other cool things that we humans do. Half a century has passed and this still didn't happen. Computer science has seen enormous progress, but we have not found an algorithm based on formal logic that could imitate intuitive human actions. I believe that we never shall, because devising an algorithm based on formal logic actually means understanding and explaining an action in terms of a fixed number of axioms.

Firstly, it is unreasonable to expect that we can precisely explain much of the real world, because, strictly speaking, there exist mathematical statements that can't in principle be explained. Secondly, and most importantly, this expectation contradicts the assumption that most "truly human" actions are intuitive, i.e. we are simply incapable of understanding them.

Now what follows is a strange conclusion. There is no doubt that sooner or later computers will get really good at performing "truly human" actions, the trend is clear already. But, contradictory to our expectations, the fact that we shall create a machine that acts like a human will not really bring us closer to understanding how "a human" really "works". In other words, we shall never create Artificial Intelligence. What we are creating now, whether we want it or not, is Artificial Intuition.