Holography is a fascinating way of storing and displaying visual information - one which will, hopefully, one day become as commonplace as photography and video is today. Unfortunately, at the current moment it is still a largely exotic trade, limited to artistic exhibitions or science museum displays. While the explanation of how photography works is usually part of the standard school curriculum, holography, at the same time, is often regarded as some mysterious sci-fi technology. The problem is made worse by the fact that there do not seem to be too many explanations around in the Internet, which would aim to properly dispel the aura of mystery. Here is my take at fixing that problem.
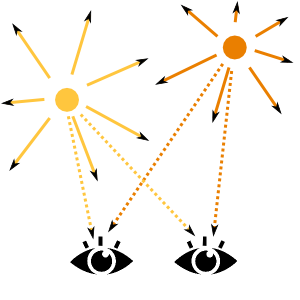
Let us start by considering the following illustration, where two hypothetical eyes are observing two hypothetical light sources.
The light from the two lamps reaches the eyes at different angles and intensities, which depend on the positions of the eyes relative to the lights. Because of that difference in angles and intensities, the brain, attached to the eyes, is capable of "triangulating" the location of the lamps, thus forming an enjoyable "three-dimensional" perception of the whole scene for itself.
Let us position a piece of glass in front of the light sources. We can regard this glass as a set of "pixels", through which light rays fly from the lamps towards the eyes. The figure below illustrates three such randomly selected "pixels" on the glass along with the directions of rays that leave them.
What if we could design a piece of glass which would fully consist of such hypothetical "pixels", with each pixel emitting two light rays in the appropriate directions? The eyes, observing such a piece of glass, would not know that the rays are really produced "in the pixels". Indeed, they perceive exactly the same light rays as if the light was coming from two lamps, positioned somewhere behind the glass. Hence, the brain, attached to the eyes, has to perform the same triangulation as the one it did when the lamps were real, and is not be able to distinguish the "fake glass" from a real scene with the lamps.
Although this idea of faking reality might look nice, the task of manufacturing small enough "pixels", which would be able to emit light in a number of given directions with given intensities and colors, is, unfortunately, technologically too complex to be practical.
This is where Physics comes to help us out. "Hey, guys," - she says, - "you are forgetting that light is not really a set of rays flying from from point A to point B along straight lines. Light is a wave. Hence, assuming that your light sources are emitting coherent light of a given frequency, a correct illustration of what happens in your scene with two lamps would be the following:"
If we now consider an arbitrary point-"pixel" on our glass, the electromagnetic waves which pass through it are perceived there in the form of some oscillation. The whole situation above could be modeled by considering waves on a water surface. To simulate the "glass" (the blue line) let us have a horizontal row of buoys float on the surface. Each of the buoys will be moving up and down in its place due to the waves, and we can record this movement.
Here comes a question: what if we remove the original two oscillation sources and instead will start "replaying" the recorded movements of the buoys buy forcing them to move up and down and thus form their own waves? The example below simulates this situation using 19 "buoys":
Does not look nice at all, does it? Now Mathematics comes along to help: "Try harder!" - she says. "If your buoys are dense enough, everything will work out!". Hence, we increase the number of buoys and try again:
Indeed, now we observe how a row of oscillating buoys (an analogue of a "glass" in our model) is generating a wave in front of it, which is completely identical to the one that was produced when two sources were oscillating behind it. No matter where we position ourselves in front of the buoy row, our perception will happily fool us into thinking that the wave we see is really a result of two point sources oscillating somewhere in a distance. Our brain will even help us to estimate the exact position of those sources somewhere behind the row. He does not know he is being fooled. Try covering the upper half of the animation above to get a better understanding of this illusion.
Hence, if we can make a glass, which consists of "pixels" each of which could "record" a profile of a light wave and then be able to reproduce it, the "image" observed by looking at such glass would be perfectly identical to an image that would be observed if the glass would simply pass through it the light from some sources located behind it. But is it possible? Isn't asking each "pixel" to record an arbitrary oscillation too much?
Here is when Mathematics comes along to help again. "Do you want to see a magic trick?" - she asks. "Yes!" - we answer.
Remember that you have two light sources emitting waves behind your piece of glass. As we agreed, they are emitting coherent light, i.e. light of the same frequency (for example, you could shine a laser light on the two points and have them reflect this light). Now let us see what happens at one of the pixels-"buoys" of your glass.
This point receives light waves from both sources. As the distances to the two sources are different, the two light waves reach the pixel with different intensities and phases. Formally, suppose the wave from the first source reaches the pixel with amplitude ![]() and phase
and phase ![]() and the wave from the second source reaches the pixel with amplitude
and the wave from the second source reaches the pixel with amplitude ![]() and phase
and phase ![]() . The two waves add up, so the pixel "feels" the overall oscillation of the form
. The two waves add up, so the pixel "feels" the overall oscillation of the form
![]()
Now if you have not two, but three, four, ten, or a million of point sources behind the glass, the arriving signal will be, correspondingly, a sum of three, four, ten, or even a million sinewaves with different amplitudes and phases.
Now here comes the trick, hold your breath: Sum of any number of such sinewaves is itself just a single sinewave with some amplitude and phase.
In other words, even if there is a million point sources emitting coherent light from behind the glass, each "pixel-buoy" of our glass will still perform a simple oscillation of the form ![]() . Hence, to "record" the oscillation of each "pixel-buoy" we must store only two parameters: its intensity and phase.
. Hence, to "record" the oscillation of each "pixel-buoy" we must store only two parameters: its intensity and phase.
Now everything starts to look much simpler. Storing light intensity of a pixel is simple - any photograph does that. Dark spots on a photo or a screen emit (or reflect) low intensity light, white spots emit high intensity. It only remains to store the phase. Several methods have been proposed for that. Conceptually the simplest one (but technologically the most advanced) makes use of particular crystals which can shift the phase of light that passes through them. Each "pixel" could then be made out of such a crystal with an appropriate phase shift coded in it. When a "glass" made of such crystals is lit from the back by a coherent light source, each pixel would introduce the necessary phase shift into the light which passes through it, and thus reproduce the necessary wave front. I presume that this HoloVisio project is relying on this idea to design a proper holographic monitor.
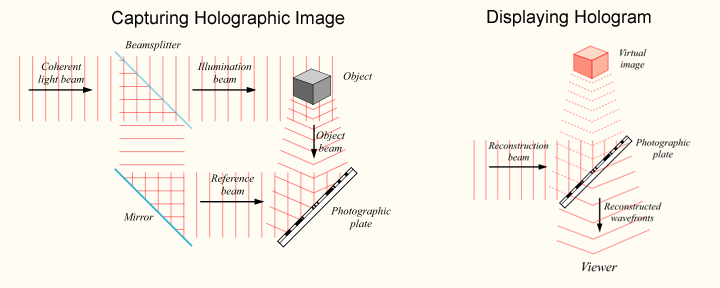
The conventional holograms, the ones you typically see in science museums, are made using a simpler principle, though. Omitting some technical details, the idea behind it is the following. Let us add to the scene a reference ray of coherent light.
Now at some pixels on our "glass" the phase of the reference ray will coincide with the phase of the light coming from the scene. The overall wave oscillation at those points will be increased. At other points the phases of the reference and the scene light will mismatch and the signal will be weakened. We can record the resulting interference pattern by storing light spots on the glass at the pixels where the phases matched and dark spots where the phases did not match.
Now, whenever we shine the reference ray again through the resulting plate, only the parts of the ray with the "correct" phase will be let through, as those are exactly the places where the glass is transparent to the reference ray. As a result, you'll obtain a decent holographic reproduction. Here's a figure from Wikipedia, illustrating this principle of recording and reproducing holograms:
Considering the speed at which our photocameras have been transitioning over the recent decades from megapixel resolutions into gigapixels and observing the fast spread of stereoscopic "3D" from movie theaters into TV-sets and portable devices, it is both surprising and sad to see no notable signs of proper holographic display technology being developed in parallel. I do hope to see mass-produced holographic displays along with appropriate software within my own lifetime, though.