Every Spring thousands of aspiring undergraduates spend numerous diligent hours working on their final theses, suffering the stress of the deadlines and the tempting pressure of the nice weather. Once they are done writing, they defend their work in public. In the end, they are graded by their supervisors, opponents and an academic committee. The grading rules might vary among universities and faculties, but their essence can be abstracted as follows: the supervisor provides a mark representing his opinion, the opponent provides a mark representing his opinion, and the final grade is obtained by taking the average of the two.
However, this process is not necessarily as simple as it looks like from the first glance. Although both the supervisor and the opponent are supposed to announce "the mark, representing their opinion", they are knowledgeable of the final grading scheme and might in fact, perhaps unconsciously, play a somewhat different game. Indeed, if the supervisor believes the student's work is worth a 4, he is in fact interested that final grade would be 4, no more and no less. The same holds for the opponent. Now let us assume that the difference between the proposed mark and the final mark measures the "penalty" for both the supervisor and the opponent. We could then regard the whole grading process as the following game.
- The supervisor has his opinion about the proper mark
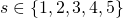 . Similarly, the opponent has his opinion about the proper mark
. Similarly, the opponent has his opinion about the proper mark 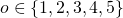 .
. - The supervisor announces the mark
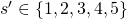 , the opponent announces the mark
, the opponent announces the mark 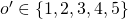 . The final grade
. The final grade 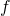 is computed as the average
is computed as the average 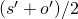 .
. - The supervisor receives penalty
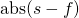 and the opponent receives penalty
and the opponent receives penalty 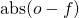 .
. - Naturally, both parties are interested in minimizing the penalty.
Now, assuming that both the supervisor and the opponent are indeed playing the above game, how would they act? Of course, this depends on their "true" opinions s and o, and whether they are knowledgeable of each other's opinion or not. For simplicity, let us first consider the case where s = o = 4 and both parties know it. In this case, we can represent the game in the traditional matrix form:
| s' | o' | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 3 | 2.5 | 2 | 1.5 | 1 |
| 2 | 2.5 | 2 | 1.5 | 1 | 0.5 |
| 3 | 2 | 1.5 | 1 | 0.5 | 0 |
| 4 | 1.5 | 1 | 0.5 | 0 | 0.5 |
| 5 | 1 | 0.5 | 0 | 0.5 | 1 |
There are three optimal solutions here — (s'=3,o'=5), (s'=4,o'=4) and (s'=3,o'=5), with the logical (4,4) choice being the "safest" for both parties in terms of the maximal possible penalty in case the opposing party presumed a different optimal solution.
Now what if s and o are different. For example, s = 4 and o = 3. In this case, the payoffs of the supervisor and the opponent are not equal any more:
| s' | o' | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 3 | 2 | 2.5 | 1.5 | 2 | 1 | 1.5 | 0.5 | 1 | 0 |
| 2 | 2.5 | 1.5 | 2 | 1 | 1.5 | 0.5 | 1 | 0 | 0.5 | 0.5 |
| 3 | 2 | 1 | 1.5 | 0.5 | 1 | 0 | 0.5 | 0.5 | 0 | 1 |
| 4 | 1.5 | 0.5 | 1 | 0 | 0.5 | 0.5 | 0 | 1 | 0.5 | 1.5 |
| 5 | 1 | 0 | 0.5 | 0.5 | 0 | 1 | 0.5 | 1.5 | 1 | 2 |
There are two Nash equilibrium solutions to this game and it is funny to see that none of them is the seemingly logical (4,3) choice. Instead, they are (5,1) and (1,5), the former being somewhat preferable to the supervisor. That means, the equilibrium strategy dictates the supervisor to suggest the mark 5 (which exceeds his opinion), to which the opponent should respond with a drastically low evaluation of 1. Looks like a rather typical thesis defence scenario, doesn't it? 🙂
Finally, when the true s and o are not known by the opponent and the supervisor correspondingly, the analysis becomes more complicated, because the players now have to assume something about the opponent. But the conclusion stays the same — whenever the supervisor has the slightest doubt that the opponent might be willing to suggest a lower mark, he will have to pick the overestimation strategy. And the opponent will then naturally tend to drastically underestimate.
By this weird post I actually wanted to express sincere congratulations to those who have succesfully defended this year, in particular my diligent bachelor students Anastasia, Karl and Riivo.





