The following text will only make sense to you if you know the technical details of Support Vector Machine learning.
Having recently had to give some lectures (1,2,3,4) and exercise sessions (1,2,3,4) on linear classification in a machine learning course, I discovered that one of the most famous linear classification methods, the classical Support Vector Machine, does not seem to be fully specified in any of the prominent reference materials. Namely, the SVM learning procedure produces two parameters: the coefficient vector 
and the bias term 
. While the problem of finding is typically explained in sufficient detail, the procedure of computing is usually swept under the carpet.
Here is, for example, what we see in the Vapnik's seminal work, the birthplace of SVMs (Section 10.2, page 411):
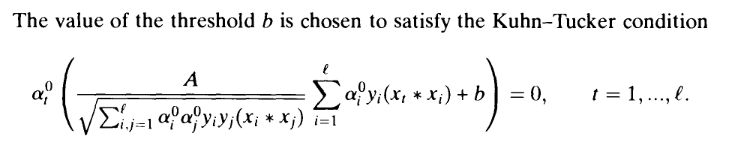According to my calculations this is plain incorrect, because the corresponding Kuhn-Tucker conditions (in the "soft margin" SVM that we are considering here) are actually:
![\[\alpha_t^0\left(\frac{1}{\gamma}\sum_{i=1}^\ell \alpha_i^0y_i(x_t * x_i) + b-1+\xi_i\right) = 0\]](https://fouryears.eu/wp-content/ql-cache/quicklatex.com-307ccd09d2869e87f9bf8e43968fc587_l3.png "Rendered by QuickLaTeX.com")
The important difference is the presence of the 
term, which is unknown, hence the equation is not useful for finding . Later on, the reader is also presented with the following summarizing description of the algorithm:
Do you see any mention of the way to compute ? I would expect the author to be somewhat more helpful with respect to this detail, which is obviously important for anyone willing to implement their own version of SVM.
OK, that was an old book, let's take a look at some newer materials. The two books which could be regarded as authoritative sources on the subject of SVMs are probably "An Introduction to Support Vector Machines" and "Kernel Methods for Pattern Analysis". Here is what the first book tells us about computing (Proposition 6.11, page 106):
This suggests that in order to compute we need to find 
, such that 
, i.e. there must exist at least one training point lying exactly on the margin. Although in most practical situations such support vectors will indeed exist, it is also theoretically possible that there won't be any, i.e. not a single support vector will lie exactly on the margin. Thus, for purposes of implementing SVMs, the provided specification is incomplete.
The same problem is present in the second book:
Take a careful look at lines 5-6, which claim that in order to compute we need to choose 
such that the corresponding 
are strictly between 0 and 
. This is not necessarily true for any 
.
So then, what is the proper, fully general way of computing ? Of course, it is not too hard to derive, and thus makes for a great course homework exercise (e.g. Exercise 4 here). If you managed to read up to this point, I presume you should be motivated enough to try solving it. If you give up, you are welcome to consult my sample solution (Exercise 4, page 7).
