Playing cards are a great tool for modeling, popularizing and explaining various mathematical and algorithmic notions. Indeed, a deck of cards is a straightforward example for a finite set, a discrete distribution or a character string. Shuffling and dealing cards represents random sampling operations. A card hand denotes information possessed by a party. Turning card face down or face up looks a lot like bit flipping. Finally, card game rules describe an instance of a particular algorithm or a protocol. I am pretty sure that for most concepts in maths or computer science you can find some card game or a card trick that is directly related to it. Here are some examples of how you can simulate a simple computing machine, illustrate inductive reasoning or explain map-reduce, in particular.
Cryptographers seem to be especially keen towards playing cards. Some cryptographic primitives could have been inspired by them. There are decently secure ciphers built upon a deck of cards. Finally, there are a couple of very enlightening card-based illustrations of such nontrivial cryptographic concepts as zero-knowledge proofs and voting protocols. The recent course on secure two-party computation given by abhi shelat at the last week's EWSCS extended my personal collection of such illustrations with another awesome example — a secure two-party protocol for computing the AND function. As I could not find a description of this protocol anywhere in the internet (and abhi did not know who is the author), I thought it was worth being written up in a blog post here (along with a small modification of my own).
The Tinder Game
Consider the situation, where Alice and Bob want to find out, whether they are both interested in each other (just as if they were both users of the Tinder app). More formally, suppose that Alice has her private opinion about Bob represented as a single bit (where "0" means "not interested" and "1" means "interested"). Equivalently, Bob has his private opinion about Alice represented in the same way. They need to find out whether both bits are "1". However, if it is not the case, they would like to keep their opinions private. For example, if Alice is not interested in Bob, Bob would prefer Alice not to know that he is all over her. Because, you know, opinion asymmetry may lead to awkward social dynamics when disclosed, at least among college students.
The following simple card game happens to solve their problem. Take five cards, so that three of them are red and two are black. The cards of one color must be indistinguishable from each other (e.g. you can't simply take three different diamonds for the reds). Deal one black and one red card to Alice, one black and one red card to Bob. Put the remaining red card on the table face up.
Now Alice will put her two cards face down to the left of the open card, and Bob will put his two cards to the right of the open card:
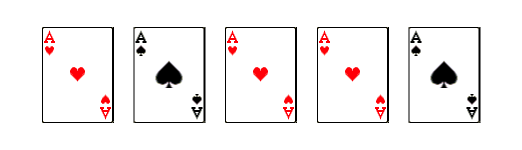
The rules for Alice and Bob are simple: if you like the other person, put your red card next to the central red card. Otherwise, put your black card next to the central one. For example, if both Alice and Bob like each other, they would play their cards as follows (albeit still face down):
Now the middle card is also turned face down, and all five cards are collected, preserving their order:
Next, Alice cuts this five-card deck, moving some number of cards from the top to the bottom (Bob should not know exactly how many). Then Bob cuts the deck (also making sure that Alice does not know how many cards he cuts). The result is equivalent to applying some cyclic rotation to the five card sequence yet neither Bob nor Alice knows how many cards were shifted in total.
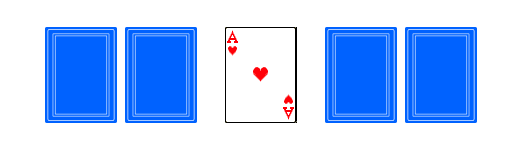
The five cards can now be opened by dealing them in order onto the table to find out the result. If there happen to be three red cards one after another in a row or two black cards one after another, Alice and Bob both voted "yes". Here is one example of such a situation. It is easy to see that it is a cyclic shift of the configuration with three red aces in the middle shown above.
Otherwise, if neither three red aces nor two black aces are side by side, we may conclude that one or both of the players voted "no". However, there is absolutely no way to find out anything more specific than that. Here is an example:
Obviously, this result could not be obtained as a cyclic shift of the configuration with three aces clumped together. On the other hand, it could have been obtained as a cyclic shift from any of the three other alternatives ("yes-no", "no-no" and "no-yes"), hence if Alice voted "no" she will have no way of figuring out what was Bob's vote. Thus, playing cards along with a cryptographic mindset helped Alice and Bob discover their mutual affection or the lack of it without the risk of awkward situations. Isn't it great?
Throwing in a Zero-Knowledge Proof
There are various ways Alice or Bob can try to "break" this protocol while still trying to claim honesty. One possible example is shown below:
Do you see what happened? Alice has put her ace upside down, which will later allow her to understand what was Bob's move (yet she can easily pretend that turning a card upside down was an honest mistake). Although the problem is easily solved by picking a deck with asymmetric backs, for the sake of example, let us assume that such a solution is somewhy unsuitable. Perhaps there are no requisite decks at Alice and Bob's disposal, or they need to have symmetric backs for some other reasons. This offers a nice possibility for us to practice even more playing card cryptography and try to secure the original algorithm from such "attacks" using a small imitation of a zero-knowledge proof for turn correctness.
Try solving it yourself before proceeding.