The recent blog post "Machine Learning in Mordor" is an excellent example of inherent bias in error estimation methods. Let us consider a standard classification task for simplicity. Then a good machine learning practice is first to find a classifier that is optimal or near-optimal on the training set. Recall that for a fixed classifier the training error is a Monte-Carlo estimate of the generalisation error - the average error that the classifier makes if the data is drawn independently from some unknown but fixed distribution. However, as soon as we choose to minimise the training error, the estimate becomes biased. The training error underestimates the generalisation error.
To avoid this the data is usually split into two separate sets: training data and validation data. If we choose the classifier according to the training data and later estimate the generalisation error on the validation data, the bias disappears and we should be in good shape. Moreover for certain classification methods, such as Support Vector Machines, it is possible to prove that the training error and the generalisation error are closely connected. That is, we can prove formulae
GeneralisationError <= TrainingError + F(n)
where F(n) is a bias term that depends on size of the training sample. Although both of these arguments are formally correct, they are actually void in certain practical settings.
For instance, student Bughrorc who split the data into a 15 element training and 5 element test set did not do anything wrong, but yet his classification algorithm is likely to perform inferior to the method proposed by Aghargh.
One could argue that Bughrorc made a mistake and used the validation set for choosing between several competing classifiers and thus, for the same reasoning as explained above, the estimate on the generalisation error is now an underestimation. However, this is only a partial explanation.
Imagine a standard no-free-lunch setting, where the labels to the data are assigned randomly so that 80% spells are good and 20% of the spells are bad. Moreover, assume that Bughrorc chooses only one classification algorithm on the training set and later uses the validation set for estimating the generalisation error. As the sample is small, the validation error might be zero again. Is the estimate free of bias now and is Bughrorc safe?
Actually not. As weird as it seems, statistical estimates depend on your intention and potential behaviour. If Bughrorc sees a small error estimate and accepts it as a correct one, it does not mean that this is unbiased eventhough the validation was properly done. To verify whether the estimate is biased or not, Bughrorc has to explore his deeper thoughts. If he can solemnly promise that a larger validation error would not had discouraged him to drop the experiment, then the validation error is indeed unbiased (but wrong). However, if a larger validation error would have stopped him from using the classifier, the same result is biased (and wrong) - whenever Bughrorc accepts the validation error it is necessarily small and thus the validation error actually underestimates the generalisation error.
As most of us are sane enough not to use a classifier with an estimated classification error near 100% or even near 50%, the validation error is biased for all practical purposes.
Surprisingly enough this bias can be estimated. Let us first fix a conservative point estimate for the validation error that is smaller than the actual generalisation error on at most 5% cases, if the validation samples are independently from the actual distribution. For example, assume that we are willing to accept the 20% classification error and the classification problem is easy - for a randomly drawn sample, the validation error is below 20 with probability 95%. Now even though we shall tend to unfairly reject all cases where the validation error overestimates the generalisation error (thus biasing our estimate towards underestimation), the fraction of such cases is at most 5/95=5.3%. Consequently, the estimate is a safe overestimate with confidence 94.7%.
On the other hand, if the classification problem is difficult, say, the validation error is below 20% with probability 4%, then the situation is completely different. Since the fraction of cases where the validation fails is larger than the fraction of cases we accept the estimate, all cases where we accept the estimate might be incorrect. Consequently, the estimate is a safe overestimate with confidence 0%.
As a final remark, note that if the validation set is small and the classification task is difficult then validation error is below accepting threshold with significant probability. For the non-free lunch Mordor case, the acceptance probability is 80% for a single point and thus we underestimate the result in 80% possible cases. If the validation set is large, then such a small error is achieved with insignificant probability and the question whether we should or should not continue does not occur "at all". In other words, the smaller is our acceptable error rate, the larger must be the validation set to compensate the rejection bias.
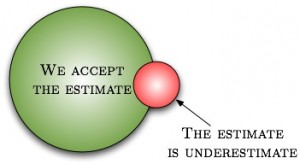
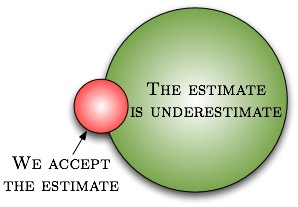






Nice! I never thought that rejection bias could, in fact be so strong as to be notable in practice. Your explanation makes it obvious that it must be the case.
Considering that this is closely related to publication bias, it is interesting whether a similar situation can be observed there? That is, the more "complicated" a published discovery/experiment is, the more likely it is to be strongly positively biased?
[...] Read the Small Print or Why All Error Estimates Are Biased [...]