The following text will only make sense to you if you know the technical details of Support Vector Machine learning.
Having recently had to give some lectures (1,2,3,4) and exercise sessions (1,2,3,4) on linear classification in a machine learning course, I discovered that one of the most famous linear classification methods, the classical Support Vector Machine, does not seem to be fully specified in any of the prominent reference materials. Namely, the SVM learning procedure produces two parameters: the coefficient vector 
and the bias term 
. While the problem of finding is typically explained in sufficient detail, the procedure of computing is usually swept under the carpet.
Here is, for example, what we see in the Vapnik's seminal work, the birthplace of SVMs (Section 10.2, page 411):
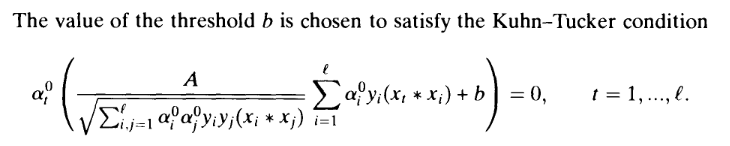According to my calculations this is plain incorrect, because the corresponding Kuhn-Tucker conditions (in the "soft margin" SVM that we are considering here) are actually:
![\[\alpha_t^0\left(\frac{1}{\gamma}\sum_{i=1}^\ell \alpha_i^0y_i(x_t * x_i) + b-1+\xi_i\right) = 0\]](https://fouryears.eu/wp-content/ql-cache/quicklatex.com-307ccd09d2869e87f9bf8e43968fc587_l3.png "Rendered by QuickLaTeX.com")
The important difference is the presence of the 
term, which is unknown, hence the equation is not useful for finding . Later on, the reader is also presented with the following summarizing description of the algorithm:
Do you see any mention of the way to compute ? I would expect the author to be somewhat more helpful with respect to this detail, which is obviously important for anyone willing to implement their own version of SVM.
OK, that was an old book, let's take a look at some newer materials. The two books which could be regarded as authoritative sources on the subject of SVMs are probably "An Introduction to Support Vector Machines" and "Kernel Methods for Pattern Analysis". Here is what the first book tells us about computing (Proposition 6.11, page 106):
This suggests that in order to compute we need to find 
, such that 
, i.e. there must exist at least one training point lying exactly on the margin. Although in most practical situations such support vectors will indeed exist, it is also theoretically possible that there won't be any, i.e. not a single support vector will lie exactly on the margin. Thus, for purposes of implementing SVMs, the provided specification is incomplete.
The same problem is present in the second book:
Take a careful look at lines 5-6, which claim that in order to compute we need to choose 
such that the corresponding 
are strictly between 0 and 
. This is not necessarily true for any 
.
So then, what is the proper, fully general way of computing ? Of course, it is not too hard to derive, and thus makes for a great course homework exercise (e.g. Exercise 4 here). If you managed to read up to this point, I presume you should be motivated enough to try solving it. If you give up, you are welcome to consult my sample solution (Exercise 4, page 7).
I usually prefer to get rid of the bias term by considering previously centered data instead. For the case of the Tikhonov regularization (squared loss function) it is straightforward to recover an optimal bias term from the resulting expansion parameters (alphas, in your case) and original means ( mu(X) and my(Y) ). I'm not sure about the SVM case (same penalty term but hinge loss, not squared) but it's potentially possible to do the same trick.
P.S: Of course I mean centering the data in feature space, i.e., centering a kernel, not in the input domain.
Yes, for L2-loss with L2-regularization, centering is equivalent to removing the bias term. For SVM's hinge loss, though, it is not the case.
Consider a simple dataset of 1-dimensional points, with two negative instances (1, 2) and two positive instances (3, 1002). The mean of those data points is 252, which is obviously not a correct bias (assuming the classifier f(x) = sign(x - b)).
The correct SVM bias would be any number between 2 and 3.
It is probably true, though, that for "good" data without bad outliers, using the mean for the SVM bias (e.g. centering the kernel) might often be a decently valid thing to do.
Yep. I agree. For purely L2 case one can recover an optimal bias
with
b = mean(Y)- mean(X)*alpha,
which is not the case for hinge or eps.-insenstitve losses.
However, I'm still curious about existence of a certain statistics fx() and fy() such that one can omit the bias by doing the following:
alpha=solveSVM(X-fx(X),Y-fy(Y),[C gamma ..])
b = fy(Y)- fx(X)*alpha;
Probably fx() and fy() may depend on C (and epsilon).
You can obviously find a proper centering of X, that will let you fit alphas correctly using a "b-free" procedure. Also, there is a way to compute b from a vector of (Y - alpha*X). However, this computation is not of the form (fy(Y) - fx(X)*alpha). Instead, it is a combination of taking min's and max's to find a range of suitable values for b.
Note that, contrarily to the L2 case, the solution for b is not unique, hence the formula of the form b := fy(Y) - alpha*fx(X) wouldn't be sufficient.
It seem that the two links at the end are no longer available. Could you please give some hints? I have been trying an entire evening trying to figure this out...
I'm also wondering why this problem doesn't come up very often, given that people may use cross-validation to tune a wide range of C values. I haven't figured out what's preventing this from happening.
Thank you!
Fixed the links, thanks.
I guess that the problem does not come up often, because there are in fact very few actual implementations of SVM around (e.g. LibSVM). Whoever decides to solve SVM "manually" (e.g. via some quadratic optimization), is usually just practicing theory, and the tiny details of "absolutely perfect implementation" do not matter as much. But if at some point you want to make your own SVM implementation, you will probably have to think of this aspect.
Thanks! This is very helpful.
I am not entirely clear about last part of the solution to Exercise 4*. "The complete solution" for b on the top of page 9 seems to just literally encode the constraint that SVs should be SVs and non-SVs should be non-SVs. It's not clear to me how the 1D geometric median of {e_s} discussed before automatically fits into this. I guess we still need to take an extra step to intersect the "median range" with the range on top of page 9?
The situation where you have to derive b from constraints only applies when there is an even number of support vectors. If there is an odd number of support vectors (which also implies there is a support vector at the margin), the solution is unique and should be found by conventional means (e.g. taking the median). Simply constraints are not enough here as they are not equivalent to the problem any more.
The reason is that if you need to find a median among an even number of elements, this is equivalent to saying "I need to find a number that is greater than any element in the first half and smaller than any element in the second half". If you have to find a median among an odd number of elements such a rephrasing does not work any more.
Hmm... I thought through it a bit more, and I guess my question can be phrased as, assuming there are odd number of support vectors, why the the median of their corresponding {e_s} necessarily falls into the b range on top of page 9? For example, since each e_s either provides an upper bound or lower bound for b, is it possible that the support vectors provide a few more such upper bounds than lower bounds, so that the median of {e_s} violate the constraints?
I'm also trying to figure out why the footnote on page 8 is correct... And does it mean we can simply rule out the case of even number of support vectors when all \alpha are either 0 or C? Then why do we need to consider the even-number case in the discussion?
Thanks so much!
In short but confusing terms, the median falls into the range because it is the last step of a multi-step optimization method, where the first step already took the constraints into account. In fact, it was the first step that determined which vectors are to be used for the median computation.
It is probably confusing, so watch the hands: as the explanation of Exercise 4 begins we already start with the solution w* for the optimization task as if we found it already. This solution already took care of all the constraints, determined which of them must old and which not, and thus told us that "the solution exists and for this solution those vectors will be the support vectors". Now we are left with the task of using this information to derive b. We then discover that any b will fit as long as it 1) is the min-absolute-value of a particular sum over the support vectors, and 2) it keeps non-support vectors away from the margin.
You ask whether it is possible for condition 1 to contradict 2. No, it is not possible because if there is only one possible b, then this one possible b with the one possible w* uniquely determines the list of support vectors: a list we obtained already and are now using to compute b. Obviously, if this list of support vectors uniquely determines b and vice-versa, the non-support vectors will stay non-support vectors once we compute this b (i.e. there is not way to violate condition 2).
The only reason for condition 2 (and the "catch" of the puzzle) is that non-support vectors can affect things when b is not unique (which is the case when the number of support vectors is even and there may be no support vectors on the margin). Suppose, for example that we are working with one-dimensional x. Let the data points be (0, -1), (1, 1), (1.2, 1). Suppose we found the solution w* = 1 (i.e. margin length is exactly 1) and the support vectors are (0) and (1), i.e. the first two data points.
(I'm lazy to draw a picture but suppose you'll be able to do it if needed).
Now we know that the separation point must go somewhere between (0) and (1) (because those are the support vectors of different classes). If we put the separation point at 0 (i.e. b=0) the first support vector violates the margin by 1, and the second is on the margin, so the overall margin violation is 1. If we locate the separation point at (1) (i.e. b = -1), the first support vector lies on the margin and the second violates it by 1, so again the overall margin violation is 1. It is easy to see that the situation is the same for any b between 0 and -1: we can shift the separation point between 0 and 1 freely and the total margin violation will stay the same, it will simply trade off between the contribution of the first and the second support vector.
So the correct b is anywhere between 0 and -1, right? No. By forgetting non-support vectors we forgot one thing - if b becomes -0.2 or lower (i.e. the separation line moves past 0.2) the third data point starts violating the margin. So, although we do have "more freedom" to choose b when we have an even number of support vectors, we should not forget about the non-support vectors.
This is the aspect, which is pretty much always omitted from textbooks.
As for the footnote: first think about the example I brought above. The only reason why you can shift b back and forth there is that shifting it increases the penalty of one support vector and decreases the penalty of the other one by the same amount. If there would be two support vectors on the left and one support vector on the right, shifting the separation line to the left by 0.1 would increase the penalty by 2*0.1 for the vectors on the left and reduce by 0.1 for the vector on the right. Hence this is suboptimal and you would rather make sure the "dominating" side of the hyperplane has at least one support vector with a penalty of 0.
Another way to see it is purely formally. The solution to the min-absolute-value problem is essentially a median. For an odd number of elements there is just one median. For even number of elements the median is not well-defined - you can pick any value between the two middle ones.
.. the case when all support vector alphas are at C is not special here. In fact, the example above (where you can shift the separation back and forth) would be such. The situation you are thinking of is probably the one where all support vectors are lying on the margin (in this case their alphas could be anything between 0 and C in fact).
Here consider the continuation of the example above, but suppose the two support vectors are at positions (0) and (2). Obviously this leaves only one place where you can position the separating line.
In terms of the median computation: you will have two e - values:
e[0] = -1 - 0 = -1
e[1] = 1 - 2 = -1.
Obviously the median of the two is uniquely defined as -1, despite the fact that there are two elements with no "middle one".
Not sure this explanation is clear without whiteboard and handwaving, but hopefully you'll decode what I mean. Nice that someone actually takes interest in this puzzle (I remember when I gave the course no student even tried to solve it).
Thanks! This does clear up a lot of my confusion. A few more questions:
This makes intuitive sense to me, but I'm still having some problem seeing this formally...
I assume "1)" refers to $b = \arg \min_{w_0} \sum_{s \in SV} |e_s - w_0|$, as on top of page 8?
But my understanding was we need to solve "1)" under the constraint of "2)", as suggested in (*) on page 7, which 1) is derived from. By simply choosing the median, "2)" is not (directly) considered. It seems that what you mean is when the unconstrained problem "1)" has a unique solution, "2)" will always be automatically satisfied. Could you please explain a bit more on this?
I'm a little confused here... I though b and w0 are just different names for the same thing... Aren't they? Or does w0 here denote the w* in the solution?
The list of SV uniquely determines b by "1)" only if we solve "1)" as an unconstrained problem without considering "2)". I'm still not sure why this is equivalent to solving "1)" constrained by "2)"...
So I guess w0 denotes w* in the solution pdf, since the geometric margin is 1 = 1/w0?
Following this example, suppose we have another point (0.8, -1), it would impossible for the support vectors to be (-1,0), (0.8, -1), (1,1), unless the solution for w were something other than 1?
I understand that having an even number of support vectors is a necessary condition for solution of b to be not unique. What I don't understand is why this is related to "margin"... maybe we are just using different terminologies? My "margin", do you mean "decision boundary"? I though a "margin" means one of the two lines on either side of the decision boundary with functional margin 1 (or, equivalently, geometric margin 1/|w|).
Yes.
Note that the median is over support vectors. If you know what points are support vectors you have essentially already solved the gist of the problem. And you surely know that there does exist a b such that y(w*x + b) <= 1 is satisfied iff x is a support vector.
Oh, sorry. When I wrote w0 I meant w*, of course. Fixed the text.
I assume there's a typo and you meant (0, -1), (0.8, -1), (1, 1) above, obviousy. No, w does not have to only be 1 for this situation.
w certainly has to be positive (because the leftmost support vector has y = -1). Also w has to be at most 2, because otherwise (0, -1) and (1, 1) could not both be support vectors. Otherwise any w inbetween could be a solution, depending on C. What you certainly know, however is that the point (0, 1) must be on the margin exactly, hence -1*w*0 + b = 1, from which you know that b must be 1. (or well, maybe that was another typo and you meant that already :))
By "margin" in this thread I mean the two lines on either side of the decision boundary with |f(x)| = 1, (located at geometric distance 1/|w| from it).
Thanks for the explanation! I think I only have one question now. ( sigh of relief... 🙂 )
I am convinced that such a b must exist, but I'm not sure why a unique solution to the unconstrained problem "1)" is necessarily such a b.
Shall I try to phrase my question more clearly? (Sorry for the $\LaTeX$ though... maybe you could copy and paste everything into https://stackedit.io/ to render)
Assume the optimal solution to be b*, then we know it must satisfy the constraint:
It's also clear that (by definition):
What I'm not sure is whether this is true:
or equivalently, whether this is true:
I think if we can establish this, then naturally the unique solution of "1)" would also be the solution to the original primal problem.
(Wow the LaTeX actually rendered in the comments!)
I think the best way to explain it is still the derivation I wrote up in the sample solution. I admit the step where I say "we can drop all terms from the sum, which correspond to non-support vectors, as those play no role" is formally shaky, and I see your confusion.
Let me try to dispel it somehow.
Consider the last equality in your comment. It is actually not true as-is. The correct version would be:
such that
Now to see why it's true. Call the left part A and the right part B. Let us solve A and define a "support vector" to be any x_i for which the corresponding term in the sum is nonzero (in fact actual support vectors are a superset of this set, but it does not change the logic). Now we turn A into a constrained optimization task, by simply adding a set of constraints, that require all the terms, corresponding to non-support vectors, to be zero. Obviosly, if the optimal b for non-constrained A already satisfied those constraints, adding them won't change matters.
Now we have a constrained optimization task where there are elements in the sum, which cannot be nonzero without violating the constraints. Clearly, dropping those terms should not affect the result then. And once we do it, we obtain B. Which means that A and B must have the same solution (both the value and the argument). QED.
As you see, taking into account the constraints for non-support vectors to remain non-support vectors is crucial for things to work out formally, and thus those must, ideally, be taken into account when computing b. You can ignore them, though, if there is at least one support vector on the margin, in which case you can compute b directly.
This is what I'm not clear about. My last comment was an attempt to justify this, but now I see why it is not correct. Let me try again to suggest another explanation and see whether it is right.
1. When there are odd number of support vectors, choosing b to be the median of {e_s}, which is the solution to the unconstrained problem "1)", will always put one of the support vectors on the margin. (Not yet sure how to formally show this.)
2. If we plug w* back into the primal form and directly solve for b (e.g. as a linear programming problem), the b we get will also put the same support vector on the margin. (As stated in the footnote of page 8, there must be a support vector sitting on the margin. I kind of see why this support vector should be the same as above, but not very sure...)
3. Therefore, when there are odd number of support vectors, solving the unconstrained problem "1)" is equivalent to solving the primal problem.
Now I am not sure what you are saying here, but I should note that step 2) (plugging w* back and solving for b) is exactly what we are discussing (it is the origin of the median solution in the first place). In this sense 1 and 2 are the same thing.
The reason why the median solution for odd number of vectors will always put at least one of the vectors on the margin is simple:
1) there *must* be one vector on the margin
2) the e_i for this vector will be exactly equal to the correct b (we could compute it directly from the condition wx + b = 1).
3) there will be equal number of vectors with e_i > b and e_i < b. Note that vectors that have e_i < b are those that are violating one margin, and those that have e_i > b are violating the other one. There can't be more violators on one side than the other (because then you could move the separating line away from the dominating side, decreasing the objective function).
The "2" in my last comment is the problem that we are trying to solve, which I think in principle can be solved using linear programming (if we are not using kernels). The "1" in my last comment is the solution proposed in "svm_solutions.pdf" when there are odd number of support vectors. I was asking why, when there are odd number of support vectors, "1" and "2" would always put the same support vector on margin, making "2" a valid way of solving "1".
I have been thinking about a pathological case and I'm not sure how it could be taken care of. Like earlier, assume the problem to be 1-dimensional. Assume from w* we know the geometric margin to be 2. We have support vectors:
y=-1: x=-1.5,-1,-0.5
y=1: x=0.5,1
Among the non-support vectors, two of them are:
y=1: x=2.01, 2.02
If we set b to the median of {e_s} of support vectors, we would put the two non-support vectors inside the margin, which violates the constraint.
Alternatively, consider the following set of support vectors (geometric margin is still 2):
y=-1: x=-1.5,-1,-0.5
y=1: x=0.5,1,2,2
Further assume the two support vectors with x=2 are right on the margin, and assume their corresponding \alpha to be zero, i.e. we don't know they are support vectors. If we again choose the median of {e_s}, these two support vectors would both have positive penalties, making the solution sub-optimal.
Thanks again for taking the time to discussing with me 🙂
Aha, I see what you mean. If you let me rephrase it in terms of my own proof, you say that "hey, in the proof you basically reformulate the problem of finding b as a min-absolute-value with condition (*). Then you somewhy forget about the condition (*) for the case where the number of support vectors is odd (claiming that taking the median is enough), and only return to it when the number of SVs is even".
I admit that formally this is certainly a hole in the proof, and right now I have no idea how to properly patch it up. Intuitively, however, I have the feeling that it is still the correct answer here.
Consider your first example. It is true that if you take the support vectors as given, it seems like you cannot position the hyperplane at 0.5, because this will "embrace" points 2.01 and 2.02 that you claim to be non-support vectors. However the problem here is due to the fact that you cannot simply pick any set of points and declare them to be support vectors - a point being a support vector is a consequence of the optimization task, not something you choose up front.
Indeed, suppose we start by positioning the separating hyperplane at 0. This will nicely embrace all the support vectors and keep non-support vectors away. Now we see that there are three negative points violating the margin and only two positive, so let us start shifting the separating line to the right to decrease the overall penalty. Ideally, we would like to do it up to the point where -1.5 reaches the margin. In your example we somehow get stuck because the point 2.01 gets in the way. "Hey you, you can't move the separating line further because Tom claims I am not a support vector so you may not let me violate the margin". But let us forget what Tom said and continue moving the separating line. The point 2.01 will enter the margin and start contributing a penalty, but the overall penalty will not increase because now there is simply equal number of violators of both classes. We move the separating line up to the point where it hits 2.02, and this is where we stop, because letting 2.02 violate the margin will now indeed increase the penalty.
Hence, in your example, all the points except 2.02 must necessarily be support vectors and the separating line can be anywhere between 0.01 and 0.02.
But again, this is largely handwaving. If we could come up with a definite proof (or rejection) on this issue it would be nice. As I mentioned, I think the core reason is due to impossibility of having an odd number of support vectors and none of them on the margin (and you can somewhat see it if you think of this "moving the boundary slowly" process I used above).
I have an idea. But before that, I would like to make an argument based on the second example I gave in my last comment. I agree with your argument about my first example, but I think it doesn't really get rid of the problem shown in the second example, which is: support vectors sitting on the margin can have zero \alpha values, preventing us from figuring out the exact number of support vectors from \alpha values.
My idea is actually quite simple: just compute the range on top of page 9, no matter the number of support vectors is odd or even; say the range is b∈[e_l, e_u]. Then try plugging both e_l and e_u into the objective function of (*). Which ever results in a smaller function value is the optimal b.
This is based on the observation that when we move the value of b from u_l to u_r, the value of the objective function either doesn't change at all, or changes monotonically (increases or decreases). Therefore the simplest thing to do would be to try both e_l and e_r 🙂
Sorry made a lot of typos in last paragraph... by u_l I mean e_l, by u_r/e_r I mean e_u
Your second example is also not perfectly convincing. Namely, a support vector cannot have a zero alpha if it affects the position of the hyperplane (if it "pushes" on it). More formally, the alpha parameter is after all the lagrangian coefficient and thus corresponds to the derivative of the lagrangian with respect to the constraint. This means, alpha tells you by how much the objective would change if you would relax the constraint (e.g. remove the point).
In your example the two points with a 2 surely contribute the the position of the hyperplane (removing them would allow to reposition the hyperplane to a lower objective function value). Hence it is impossible for them to have alpha 0 (they would have equal nonzero alphas).
The solution with checking the smaller e_l or e_u in the range is certainly correct, I believe. It is also computationally simpler than the one with the median. So it's a great idea!
I am still pretty sure though, that when there is and odd number of SVs it will always result in the same answer as taking the median, i.e. I don't think it is possible to have non-support vectors somehow prevent support vectors from positioning the hyperplane in that situation.
Hmm... can we say that training examples that falls on either margin must have non-zero α values? Otherwise in principle the problem I described wouldn't go away.
For example, let me try to modify the second example I gave as something like:
y=-1: x=-1.5,-1,-0.5,3
y=1: x=0.5,1,2,2,-3
I'm not sure how this would work out, but I am wondering whether it is possible to have wrongly classified examples that exerts enough "pull" on the margin, such that even when we remove a training example that sits on the margin nothing would change.
I also want to build a little bit on the solution I talked about last time. Recall that once we have obtained w*, the primal problem becomes
which is equivalent to
We already know that the constraints gives us some range [e_l, e_u] on top of page 9.
In addition, we can actually show that
So the problem becomes maximizing the product of b times some constant
, on the range [e_l, e_u]. Therefore, we can decide the value of b* by computing 
: if this sum is positive, then b should be e_u; if negative, then b should be e_l; if zero, any value in the range is fine.
No, I think they do not have to have non-zero alpha values, although this might be a matter of implementation (choosing which of the otherwise equal constraints is the more important one is after all not well-defined).
There is no "problem" in your example except for the fact that you tried to declare some points to be non-support vectors when in fact they were SVs.
This does not change a lot. Now you simply have two additional support vectors that heavily violate the margin.
If you run the example through R (like that, btw I fixed the links to base code on the course website, so you can try R code mentioned in the exercises, if you wish) the curious thing you'll discover is that LibSVM decides to use one of the x=2 points as a support vector and another as non-support vector. In a sense, it has all the right to do so as it is really not defined which of the two constraints is the most important one. Although I think that, strictly speaking, for the purposes of optimizing the dual (which has a sum of alpha squares), the contribution must have been split equally.
I really like the reasoning with the sum of y. It is certainly correct, and it cleanly formalizes the difference between the even and odd number of support vectors (note that this is what defines the sign of the sum).
Also, (assuming I am still right about the non-support vectors not being a problem when the number of SVs is odd), it fits my intuition: note that when there is more negative support vectors, the e_l is exactly the median. If there is more positive support vectors, e_u is the median. Otherwise you have to pick inbetween the two bounds, also taking non-SVs into account.
On a related topic, I actually decided to check how LibSVM computes the bias term. Here, line 966. Check out how it actually does compute exactly the same upper and lower bounds we are discussing. It then uses the average of ub and lb if there were no support vectors on the margin. If there were SVs on the margin, the bias is computed from the constraint directly.
During a discussion with one of my classmates, he pointed out the following: Given that
, when 
, we always get 
, therefore we can always choose any value in the range [e_l, e_u]. This conforms to both your argument and the implementation of LibSVM 🙂
How funny! Just two weeks ago I was doing svm on an assignment (not as nice an assignment as yours), and we had this issue. Our prof, however, gave us a tip in one of his many scattered slides: compute the mean of the results you would get for choosing each x as the one to solve for. For the assignment dataset, this paid off: depending on the choice of x to use to solve for b, the result would fluctuate by up to 0.5 (!) in either direction because of numerical instability.
These are very useful notes, thanks!
Although the primal SVM cost function (with Hinge loss) is not continuous, gradient descent methods have shown to work well in practice. In my experience, (L-)BFGS method converges very fast and gives a very similar result with implementations like libsvm.
So, assuming that using the BFGS method is OK for solving the SVM, can we handle the bias term by adding a bias feature to the examples (i.e. x_new = [x;1]) and excluding the weight of the bias in regularization? That is,
0.5||w(1:end-1)||^2 + C\sum( hinge(w,x_i,y_i) )
?
This is the "primal formulation", and, of course, here you "automatically" obtain the bias term by solving the optimization problem using any generic method of your choice.
The "bias term puzzle" appears when you perform a textbook-style switch to the dual formulation, which usually "forgets" about the b.
Note that although SVM is quite useful in its primal form, and there are indeed quite efficient gradient-based optimizers for it (e.g. liblinear), the dual form is no less important, as it comes along with all the "kernel method" benefits.
Hi, fascinating post & discussion, but the link at the end to 'sample solution' is no longer working? This would provide the missing key for understanding the discussion above (e_l, e_u) and would be greatly appreciated.
I took the solution offline because we had a re-run of the course this semester. It is accessible again now.
Brilliant, thanks.