Four Years Remaining

Update from year 2017: The tool described in this post DOES NOT WORK with recent versions of Skype. Either these versions stopped saving removed messages altogether, or they are doing it in a novel manner not recognized by the tool.

In other words - you would only recover "removed" messages if you are running older version of Skype (or these messages were sent at the time you were using that older version).

Yesterday I happened to attend a discussion about the security and privacy of information stored locally in Skype and Thunderbird profiles. It turns out, if you obtain a person's Skype profile directory, you will be able to log in as him without the need to know the password. In addition, Dominique made a remark that Skype does not really delete the messages that are marked as "removed" in the chat window. I found that curious and decided to take a closer look.

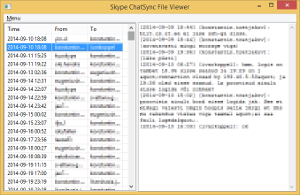
Indeed, there is a bunch of *.dat files in the chatsync subdirectory of the Skype's profile, which preserve all messages along with all their edits or deletions. Unfortunately, the *.dat files are in some undocumented binary format, and the only tool I found for reading those lacks in features. However, hacking up a small Python parser according to what is known about the format, along with a minimalistic GUI is a single evening's exercise, and I happened to be in the mood for some random coding.

Skype Chatsync Viewer

Now, if you want to check out what was that message you or your conversation partner wrote before it was edited or deleted, this package will help. If you are not keen on installing Python packages, here is a standalone Windows executable.

I haven't updated this blog for quite some time, which is a shame. Before I resume I wanted to reproduce here a couple of my old posts from other places. This particular piece stems from a post on our research group's webpage from more than 8 years ago, but is about an issue that never stops popping up in practice.

Precision of floating point numbers is a very subtle issue. It creeps up so rarely that many people (me included) would get it out of their heads completely before stumbling upon it in some unexpected place again.

Indeed, most of the time it is not a problem at all, that floating point computations are not ideally precise, and no one cares about the small additive noise that it produces, as long as you remember to avoid exact comparisons between floats. Sometimes, however, the noise can severely spoil your day by violating the core assumptions, such as "distance is always greater than zero", or "cosine of an angle never exceeds 1".

The following is, I think, a marvelous example, discovered by Alex, while debugging an obscure problem in one Python program. The choice of the language is absolutely irrelevant, however, so I took the liberty of presenting it here using Javascript (because this lets you reproduce it in your browser's console, if you wish). For Python fans, there is an interactive version available here as well.

A cosine distance metric is a measure of dissimilarity of two vectors, often used in information retrieval and clustering, that is defined as follows:

A straightforward way to put this definition into code is, for example, the following:

function length(x) {
    return Math.sqrt(x[0]*x[0] + x[1]*x[1]);
}

function cosine_similarity(x, y) {
    return (x[0]*y[0] + x[1]*y[1])/length(x)/length(y);
}

function cosine_distance(x, y) {
    return 1 - cosine_similarity(x, y);
}

Now, mathematically, the cosine distance is a valid distance function and is thus always positive. Unfortunately, the floating-point implementation of it presented above, is not the same. Check this out:

> Math.sign(cosine_distance([6.0, 6.0], [9.0, 9.0]))
< -1

Please, beware of float comparisons. In particular, think twice next time you use the sign() function.