Four Years Remaining

Every once in a while I happen to find myself in a public network, where all access besides HTTP and HTTPS is blocked by the firewall. This is extremely inconvenient, as I routinely need to access SSH, VPN or other ports besides HTTP(S). Over time I have developed a reasonably fast and simple way of overcoming the restriction whenever I need it. Let me document it here.

Google Cloud Shell

There are probably hundreds of cloud providers nowadays, each of them trying to outcompete the others by offering better, cheaper, faster, or more diverse set of services. One killer feature of the Google Cloud platform is its cloud shell, which gives you command-line access to a tiny Linux virtual machine directly from their webpage for free:

Once you are logged into Google Cloud platform you may open the shell window via this button

Even if you do not have any serious use for a cloud provider, the cloud shell is one good reason to get an account at the Google Cloud platform. Because whenever I find myself locked out of SSH behind a paranoid firewall, I can still SSH into any of my servers via the cloud shell. This works even when your access is limited to an HTTP proxy server.

Once upon a time there was a great service named koding.com, which also provided free access to a Linux console via HTTP. Unfortunately, they have changed their pricing model since then and do not seem to have any similar free offerings anymore. If you know any alternative services that offer a web-based shell access to a Linux VM for free, do post them in the comments.

OpenVPN via HTTPS

Sometimes SSH access offered by the cloud shell is not enough. For example, I would often need to access the company's VPN server. It runs on port 1194 and in a properly paranoid network this port is, of course, also blocked. The way to sneak through this restriction is the following.

1. Launch a server in the cloud, running an OpenVPN service on port 443 (which corresponds to HTTPS). Even the most paranoid firewalls would typically let HTTPS traffic through, because otherwise they would block most of the web for their users.
2. Connect to that VPN server and tunnel all traffic through it to the outside world.
3. Now we are free to connect anywhere we please. In particular, we may open a VPN tunnel to the company's server from within that "outer" VPN tunnel.
4. At this point I would sometimes SSH into a machine behind the company's VPN and never cease to be amused by the concept of having a SSH tunnel within a VPN tunnel within another VPN tunnel.

Let us now go through all these steps in detail.

Setting up an OpenVPN server

We start by launching a machine in the cloud. You are free to choose any cloud provider here, but as we are using Google's cloud shell already anyway (we are working behind a paranoid firewall already, remember), it makes sense to launch the server from Google's cloud as well. This can be as simple as copy-pasting the following command into the same cloud shell prompt:

gcloud compute instances create openvpn-server --zone=europe-west3-a --machine-type=f1-micro --tags=https-server --image=ubuntu-1604-xenial-v20180405 --image-project=ubuntu-os-cloud --boot-disk-size=10GB --boot-disk-type=pd-standard --boot-disk-device-name=openvpn-server

(obviously, detailed documentation of Google cloud functionality is way beyond the scope of this blog post. All the necessary references and tutorials are rather easy to find, though).  You may play with some of the settings passed to the command above, however the choice of the ubuntu-1604-*** image is important, because the script from the next part was only ever tested on that Linux version. The chosen machine type (f1-micro) is the cheapest and should cost around 5 euros per month (if you keep it open constantly), or a matter of cents, if you only use it for some hours.

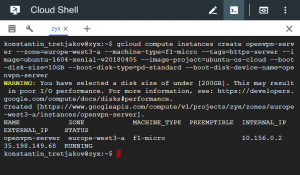
Launching a machine in the cloud

Once the machine is up, we SSH into it by typing:

gcloud compute ssh openvpn-server

Here we'll need to install and configure the OpenVPN server. This may be a fairly lengthy process of following step-by-step instructions from, for example, this well-written tutorial. Luckily, I've gone through this already and wrote down all the steps down into a replayable script, which seems to work fine so far with the chosen Linux image. Of course, there's no guarantee it will continue working forever (some rather loose configuration editing is hard-coded there). However, as we have just launched a throwaway virtual server, the worst that can happen is the need to throw that server away if it breaks. (Do not run the script blindly on a machine you care about, though). So let's just download and run it:

curl -s https://gist.githubusercontent.com/konstantint/08ab09202b68e4e3542622e99d21a82e/raw/1a3ee68008d5b565565ebb8c126ae68a8cebe549/ovpn_setup.sh | bash -s

Once completed, the script prints the filename "/home/<username>/client-configs/files/client1.ovpn". This is the name of the file which we need to transfer back to our computer. A clumsy, yet fast and straightforward way is to simply copy-paste its contents from the shell into a local text file:

cat /home/your_username/client-configs/files/client1.ovpn

We then select all the output starting from the first lines of the file

client
dev tun
proto tcp
...

all the way down to

...
-----END OpenVPN Static key V1-----
</tls-auth>

(holding "shift", scrolling and clicking the mouse helps).

We then create a new file (on the local machine), name it client1.ovpn (for example), paste the copied text and save. That's it, we have successfully set up an OpenVPN server running on port 443. Type exit in the cloud shell to log out of the server as we don't need to configure anything there.

Setting up an OpenVPN client

Next we must set up an OpenVPN client on the local computer. I am using a Windows laptop, hence the instructions are Windows-specific, although the logic for Linux or Mac should be rather similar. First, install OpenVPN. The nicest way to do it in Windows is via Chocolatey. Open cmd.exe with administrative privileges and:

1. Install Chocolatey, if you still don't have it (trust me, it's a good piece of software to have):

@"%SystemRoot%\System32\WindowsPowerShell\v1.0\powershell.exe" -NoProfile -InputFormat None -ExecutionPolicy Bypass -Command "iex ((New-Object System.Net.WebClient).DownloadString('https://chocolatey.org/install.ps1'))" && SET "PATH=%PATH%;%ALLUSERSPROFILE%\chocolatey\bin"

2. Now install OpenVPN (if you still don't have it):

choco install -y openvpn

3. Launch OpenVPN GUI (Windows button + type "OpenV" + Enter), right-click on the newly appeared tray icon, select "Import File..." and choose the client1.ovpn file we created:

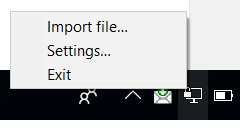
Import OVPN file

4. Once you've done it, the OpenVPN tray menu will offer you a "Connect" option (or a "client1" submenu with a "Connect" option if you have other connections configured already). Click it, observe the connection dialog, wait until the tray icon becomes green, and congratulations, all your traffic is now tunneled through port 443 of the cloud machine you launched some minutes ago.

Connected

You may verify the effect by googling the words "my ip". You are now also free to connect to any ports or services you need.

Tunnel in a Tunnel

As I mentioned in the beginning, having freed myself from the firewalls of a paranoid network administrator, I would then sometimes need to connect to a corporate or a university VPN. This happens to be surprisingly easy (this part is, however, Windows specific - I am not sure how an equivalent action should look like on Linux or Mac, although I'm sure it should be possible).

1. OpenVPN uses a virtual network tunnel adapter to forward traffic. Initially it only installs one such adapter, but if you want to run a tunnel within a tunnel you will need to add a second one. This is done by simply running C:\Program Files\TAP-Windows\bin\addtap.bat with administrator privileges. It only needs to be done once, of course (unless you need to run a tunnel within a tunnel within a tunnel - then you need to add a a third TAP adapter by running addtap.bat again).
2. Now running a VPN within a VPN is simply a matter of asking OpenVPN to "Connect" to VPNs in the appropriate order. As we are already connected to client1, we simply connect to another profile without disconnecting the first one - this will happily forward a tunnel through an existing tunnel. Fun, right?

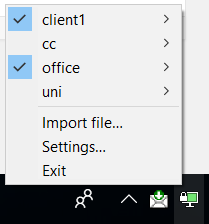
VPN via VPN

Cleaning Up

If you only needed the VPN temporarily, do not forget to destroy the cloud machine before going home - otherwise you'll have to pay the unnecessary costs of keeping a server up. Destroying servers is simple. Just go back to the cloud shell where we launched the server and run:

gcloud compute instances delete openvpn-server

That's it. You are back at the mercy of the firewalls.

The Dark Side of the Bitcoin

Recall that Bitcoin is a currency, i.e. it is a technology, which aims to provide a store of value along with a payment medium. With all due respect to its steadily growing adoption, it would be fair to note that it is not very good at fulfilling either of these two functions currently. Firstly, it is not a very reliable store of value due to extreme volatility in the price. Secondly, and most importantly, it is a mediocre payment medium because it is slow and expensive.

A typical transfer costs around $2 nowadays and takes about an hour for a full confirmation (or longer, if you pay a smaller fee). When you need to transfer a million dollars, this looks like a reasonable deal. When you buy a chocolate bar at a grocery store (something one probably does more often than transferring a million), it is unacceptable. Any plain old bank's payment card would offer a faster and cheaper solution, which is ironic, given that Bitcoin was meant to be all friendly, distributed and free (as in freedom) while banks are, as we all know, evil empires hungry for our money, flesh and souls.

The irony does not end here. The evil banks typically provide some useful services in exchange for the fees they collect, such as an online self-service portal, 24h support personnel, cash handling and ATMs, some security guarantees, interests on deposits, etc. The friendly Bitcoin offers nothing of this kind. What is Bitcoin wasting our money on then? Electricity, mainly! The Proof of Work (PoW) algorithm employed in the Bitcoin's blockchain requires the computation of quintillions of random, meaningless hashes to "confirm" payments. The "miner" nodes, running the Bitcoin's network are collectively performing more than 5 000 000 000 000 000 000 (five quintillion or five exa-) hash computations every second, continuously consuming as much electricity as the whole country of Turkmenistan. The situation is even worse if you consider that Bitcoin is just one of many other "coins" built upon the PoW algorithm (Ethereum and Litecoin being the two other prominent examples), and their overall power consumption is only growing with each day.

Just think of it: most of the $2 fee a Bitcoin user needs to pay for a transaction will neither end up as someone's wage nor make a return on investment in someone's pocket. Instead, it will burn up in fossil fuels which generate power for the "miners", wasting precious resources of our planet, contributing to global warming and pushing poor polar bears faster towards extinction. Is all this mayhem at least a "necessary evil"? Sadly, it is not.

The Unnecessary Evil

Formally speaking, Proof of Work is an algorithm for achieving consensus among a distributed set of nodes which collectively maintain a common blockchain. Is it the only such algorithm? Of course not! Many alternative methods exist, most of them (if not all) are both faster and less energy-hungry. In fact, the only valuable property of PoW is its ingenious simplicity. In terms of implementation it may very well be among the simplest distributed blockchain consensus algorithms ever to be invented.

It is natural that a successful pioneering technology (such as the Bitcoin) is originally built from simple blocks. Progress comes in small steps and you cannot innovate on all fronts at once, after all. There must come a time, however, when the limitations of the initially chosen basic blocks become apparent and the technology gets upgraded to something more efficient. With more than $1 billion dollars in electricity bills paid by Bitcoin users last year for the inefficiency of PoW, Bitcoin has long surpassed this turning point, in my opinion.

Unfortunately, due to its pioneering status, enormous inertia, ongoing hype and the high stakes involved, Bitcoin continues to roll on its old wooden proof-of-work wheels with no improvement in sight, somewhy still being perceived as the leader in the brave new world of cryptocurrencies.

Are nearly-instant and nearly-free payment along with energy efficiency too much to ask from a real "currency of the future"? I do not think so. In fact, Bitcoin could be such a currency, if only it could switch from the evil Proof of Work to a different, fast and eco-friendly consensus algorithm.

Which algorithm could it be? Let me offer you an overview of some of the current options I am personally aware of, so you could decide for yourself.

The Eco-Friendly Blockchain Consensus

Consider a network of many nodes, which needs to maintain a common state for a chain of blocks. There seem to be roughly three general categories of algorithms which the nodes could employ for their purpose: Proof of Authority (PoA), Nakamoto Consensus, and Byzantine Fault Tolerance (BFT). Let us consider them in order.

Proof of Authority

Perhaps the most straightforward solution would be to nominate a fixed subset of nodes as "authoritative", and let any of them append new blocks by signing them cryptographically. To avoid conflicting updates, nodes may agree on a predefined round-robin signing order, honestly randomize their waiting intervals, or use some kind of a deterministic lottery for selecting the signer for next block, etc.

As this approach relies on a fixed subset of (reasonably) trusted nodes, it does not look robust and secure enough for a proper worldwide distributed blockchain. For example, in the limit case of a single trusted party it is equivalent to using a single service provider such as a bank. None the less, it is a convenient baseline and an important primitive, actually applicable to a wide range of real-life blockchain deployments. By relying on a set of well-behaving parties, a PoA blockchain actually sidesteps most of the complexities of a real distributed algorithm, and can thus be made to perform much faster than any of the "truly distributed" algorithms.

The Ethereum software provides an implementation of this approach for those who want to run private chains. PeerCoin relies on the PoA principle by having "checkpoint blocks" signed regularly by a trusted authority. Finally, the Delegated Proof of Stake algorithm makes PoA work on a larger scale by relying on voting. It is probably one of the most interesting practical implementations of the idea.

Delegated Proof of Stake

Delegated Proof of Stake (DPoS) is a consensus algorithm implemented in Graphene-based blockchains (BitShares, Steem, EOS). It is a variant of Proof of Authority, where the small set of authoritative delegate nodes is elected by voting. When electing the delegates, each node can cast the number of votes, proportional to their account value (or "stakeholder share"), thus "delegating their stake in the network". The elected authorities then participate in a simple and fast round-robin block confirmation with each node given a two second window for confirming the next block.

The security of DPoS hinges on the assumption that the nodes with the most stake in the system should generally manage to elect a set of reasonable authorities, and in case of errors, the misbehaving authorities will not cause too much trouble and will be quickly voted out. At the same time, being internally a PoA implementation, the DPoS-based blockchains are by an order of magnitude faster in terms of transaction throughput than any other currently running public blockchains. Notably, they can also naturally support fee-less transactions.

Nakamoto Consensus

Consider the variation of PoA, where there are no pre-selected trusted nodes (i.e. all nodes may participate in the algorithm). Each time a new block needs to be added to the chain, let us pick the node who will gain the right to add it according to some deterministic "lottery" system. The consensus can then be achieved by simply verifying that the resulting blockchain is conforming to the lottery rules at all times, and the conflicting chains are resolved by always preferring the "harder" chain (according to some notion of "hardness").

For example, the infamous Proof-of-Work is an example of such a method. The "lottery" here is based on the ability of a node to find a suitable nonce value. The "hardness" is simply the length of the chain. Such "lottery" methods are sometimes referred to as "Nakamoto consensus algorithms". In terms of efficiency, Nakamoto consensus algorithms are among the slowest consensus algorithms.

Several alternatives to the "PoW lottery" have been proposed. Let us review some of them.

Proof of Stake

Proof of Stake (PoS), first implemented in the Nxt cryptocurrency, is a Nakamoto consensus technique, where the nodes with a greater balance on their account are given a higher chance to "win the lottery" and sign the next block. The actual technique used in Nxt is the following: before signing a block every node obtains a pseudo-random "lottery ticket number" by hashing the last block data with its own identifier. If this number is smaller than

(where is a block-specific constant), the node gets the right to sign the next block. The higher the node's balance, the higher is the probability it will get a chance to sign. The rationale is that nodes with larger balances have more at stake, are more motivated to behave honestly, and thus need to be given more opportunities to participate in generating the blockchain.

Proof of Stake is typically considered as the primary alternative to Proof of Work without all the wasteful computation, and it should, in principle, be possible to transition the whole blockchain from the latter to the former. In fact, this is what may probably happen to Ethereum eventually.

Proof of Space

In Proof of Space (PoSpace), a consensus mechanism implemented in Burstcoin, the "miners" must first pre-generate a set of "lottery ticket numbers" in a particular manner for themselves, save these numbers on a hard drive and commit the hash (the Merkle tree root) of this complete ticket set to the blockchain. Then, similarly to Proof of Stake, by hashing the last block's data, a miner deterministically picks one of his own "lottery tickets" for the next block. If the value of this ticket, discounted by the number of tickets in possession, is small enough, the miner gets the right to sign the block. The more tickets a miner generates and stores, the better are his chances. When signing the block, the miner must present a couple of special hashes which he can only know if he constantly stores his complete set of tickets (or fully recomputes a large part of it every time, which is impractical). Consequently, instead of spending energy on the "mining" process, the nodes must constantly dedicate a certain amount of disk space to the algorithm.

Although it is probably among the less widely known methods, from both technical and practical standpoint, it is one of the most interesting techniques, in my opinion. Note how it combines the properties of PoS (speed and energy efficiency) with those of PoW (ownership of a real-world resource as a proxy for decentralization).

Proof of Burn

The idea behind Proof of Burn is to allow the nodes to generate their "lottery ticket numbers" by irretrievably transferring some coins to a nonexistent address and taking the hash of the resulting transaction. The resulting hash, scaled by the amount of coins burned, can then be used to gain the right to sign blocks just like in other Nakamoto lottery systems. The act of wasting coins is meant to be a virtual analogue of spending electricity on PoW mining, without actually spending it. Blockchains based purely on Proof of Burn do not seem to exist at the moment. However, the technique can  be used alongside PoW, PoS or other approaches.

Proof of Elapsed Time

Presumably, some Intel processors have specialized instructions for emitting signed tokens, which prove that a given process called a particular function a certain period of time ago. The Hyperledger project proposes to build a consensus algorithm around those. Each "miner" will gain the right to sign a block after it waits for a certain period of time. The token which proves that the miner did in fact wait the allotted time, would act as a winning lottery ticket. I do not see how this method could work outside of the trusted Intel-only environment or how is it better than a trivialized Proof of Stake (not sure I even understood the idea correcty), but I could not help mentioning it here for completeness' sake.

Hybrid Nakamoto Consensus Systems

Some systems interleave PoW and PoS confirmations, or add PoA signatures from time to time to lock the chain or speed-up block confirmations. In fact, it is not too hard to invent nearly arbitrary combinations of delegation, voting, payments, authorities and lotteries.

Byzantine Fault Tolerance

The Practical Byzantine Fault Tolerance (PBFT) algorithm offers an alternative solution to the consensus problem. Here the blockchain state is tracked by a set of "bookkeeping" nodes, which constantly broadcast all changes among themselves and consider a change reliably replicated when it is signed and confirmed by given quorum (e.g. 2/3) of the bookkeepers. The algorithms of this type can be shown to be reliable if no more than a third of the nodes are dishonest. The Ripple, Stellar and Antshares are examples of blockchains based on such techniques. This algorithm allows much higher transaction throughputs than Nakamoto consensus (PoW, PoS, PoSpace), yet it still lags behind the speed of PoA or DPoS.

The following is an expanded version of an explanatory comment I posted here.

Alice's Diary

Alice decided to keep a diary. For that she bought a notebook, and started filling it with lines like:

Alice did her best to keep a meticulous account of events, and whenever she had a discussion with friends about something that happened earlier, she would quickly resolve all arguments by taking out the notebook and demonstrating her records. One day she had a dispute with Bob about whether she lent him $250 earlier or not. Unfortunately, Alice did not have her notebook at hand at the time of the dispute, but she promised to bring it tomorrow to prove Bob owed her money.

Bob really did not want to return the money, so that night he got into Alice's house, found the notebook, found line 132 and carefully replaced it with "132. Kissed Dave". The next day, when Alice opened the notebook, she did not find any records about money being given to Bob, and had to apologize for making a mistake.

Alice's Blockchain

A year later Bob's conscience got to him and he confessed his crime to Alice. Alice forgave him, but decided to improve the way she kept the diary, to avoid the risk of forging records in the future. Here's what she came up with. The operating system Linups that she was using had a program named md5sum, which could convert any text to its hash - a strange sequence of 32 characters. Alice did not really understand what the program did with the text, it just seemed to produce a sufficiently random sequence. For example, if you entered "hello" into the program, it would output "b1946ac92492d2347c6235b4d2611184", and if you entered "hello " with a space at the end, the output would be "1a77a8341bddc4b45418f9c30e7102b4".

Alice scratched her head a bit and invented the following way of making record forging more complicated to people like Bob in the future: after each record she would insert the hash, obtained by feeding the md5sum program with the text of the record and the previous hash. The new diary now looked as follows:

Now each record was "confirmed" by a hash. If someone wanted to change the line 132 to something else, they would have to change the corresponding hash (it would not be 1010 anymore). This, in turn, would affect the hash of line 133 (which would not be 8204 anymore), and so on all the way until the end of the diary. In order to change one record Bob would have to rewrite confirmation hashes for all the following diary records, which is fairly time-consuming. This way, hashes "chain" all records together, and what was before a simple journal became now a chain of records or "blocks" - a blockchain.

Proof-of-Work Blockchain

Time passed, Alice opened a bank. She still kept her diary, which now included serious banking records like "Gave out a loan" or "Accepted a deposit". Every record was accompanied with a hash to make forging harder. Everything was fine, until one day a guy named Carl took a loan of $1000000. The next night a team of twelve elite Chinese diary hackers (hired by Carl, of course) got into Alice's room, found the journal and substituted in it the line "143313. Gave out a $1000000 loan to Carl" with a new version: "143313. Gave out a $10 loan to Carl". They then quickly recomputed all the necessary hashes for the following records. For a dozen of hackers armed with calculators this did not take too long.

Fortunately, Alice saw one of the hackers retreating and understood what happened. She needed a more secure system. Her new idea was the following: let us append a number (called "nonce") in brackets to each record, and choose this number so that the confirmation hash for the record would always start with two zeroes. Because hashes are rather unpredictable, the only way to do it is to simply try out different nonce values until one of them results in a proper hash:

To confirm each record one now needs to try, on average, about 50 different hashing operations for different nonce values, which makes it 50 times harder to add new records or forge them than previously. Hopefully even a team of hackers wouldn't manage in time. Because each confirmation now requires hard (and somewhat senseless) work, the resulting method is called a proof-of-work system.

Distributed Blockchain

Tired of having to search for matching nonces for every record, Alice hired five assistants to help her maintain the journal. Whenever a new record needed to be confirmed, the assistants would start to seek for a suitable nonce in parallel, until one of them completed the job. To motivate the assistants to work faster she allowed them to append the name of the person who found a valid nonce, and promised to give promotions to those who confirmed more records within a year. The journal now looked as follows:

A week before Christmas, two assistants came to Alice seeking for a Christmas bonus. Assistant Jack, showed a diary where he confirmed 140 records and Mary confirmed 130, while Mary showed a diary where she, reportedly, confirmed more records than Jack. Each of them was showing Alice a journal with all the valid hashes, but different entries! It turns out that ever since having found out about the promotion the two assistants were working hard to keep their own journals, such that all nonces would have their names. Since they had to maintain the journals individually they had to do all the work confirming records alone rather than splitting it among other assistants. This of course made them so busy that they eventually had to miss some important entries about Alice's bank loans.

Consequently, Jacks and Mary's "own journals" ended up being shorter than the "real journal", which was, luckily, correctly maintained by the three other assistants. Alice was disappointed, and, of course, did not give neither Jack nor Mary a promotion. "I will only give promotions to assistants who confirm the most records in the valid journal", she said. And the valid journal is the one with the most entries, of course, because the most work has been put into it!

After this rule has been established, the assistants had no more motivation to cheat by working on their own journal alone - a collective honest effort always produced a longer journal in the end. This rule allowed assistants to work from home and completely without supervision. Alice only needed to check that the journal had the correct hashes in the end when distributing promotions. This way, Alice's blockchain became a distributed blockchain.

Bitcoin

Jack happened to be much more effective finding nonces than Mary and eventually became a Senior Assistant to Alice. He did not need any more promotions. "Could you transfer some of the promotion credits you got from confirming records to me?", Mary asked him one day. "I will pay you $100 for each!". "Wow", Jack thought, "apparently all the confirmations I did still have some value for me now!". They spoke with Alice and invented the following way to make "record confirmation achievements" transferable between parties.

Whenever an assistant found a matching nonce, they would not simply write their own name to indicate who did it. Instead, they would write their public key. The agreement with Alice was that the corresponding confirmation bonus would belong to whoever owned the matching private key:

To transfer confirmation bonuses between parties a special type of record would be added to the same diary. The record would state which confirmation bonus had to be transferred to which new public key owner, and would be signed using the private key of the original confirmation owner to prove it was really his decision:

In this example, record 284 transfers bonus for confirming record 132 from whoever it belonged to before (the owner of private key 6669, presumably Jack in our example) to a new party - the owner of private key 1111 (who could be Mary, for example). As it is still a record, there is also a usual bonus for having confirmed it, which went to owner of private key 4442 (who could be John, Carl, Jack, Mary or whoever else - it does not matter here). In effect, record 284 currently describes two different bonuses - one due to transfer, and another for confirmation. These, if necessary, can be further transferred to different parties later using the same procedure.

Once this system was implemented, it turned out that Alice's assistants and all their friends started actively using the "confirmation bonuses" as a kind of an internal currency, transferring them between each other's public keys, even exchanging for goods and actual money. Note that to buy a "confirmation bonus" one does not need to be Alice's assistant nor register anywhere. One just needs to provide a public key.

This confirmation bonus trading activity became so prominent that Alice stopped using the diary for her own purposes, and eventually all the records in the diary would only be about "who transferred which confirmation bonus to whom". This idea of a distributed proof-of-work-based blockchain with transferable confirmation bonuses is known as the Bitcoin.

Smart Contracts

But wait, we are not done yet. Note how Bitcoin is born from the idea of recording "transfer claims", cryptographically signed by the corresponding private key, into a blockchain-based journal. There is no reason we have to limit ourselves to this particular cryptographic protocol. For example, we could just as well make the following records:

This would be an example of a collective deposit, which may only be extracted by a pair of collaborating parties. We could generalize further and consider conditions of the form:

Here could be any predicate describing a "contract". For example, in Bitcoin the contract requires to be a valid signature, corresponding to a given public key (or several keys). It is thus a "contract", verifying the knowledge of a certain secret (the private key). However, could just as well be something like:

which would be a kind of a "future prediction" contract - it can only be evaluated in the future, once record 42000 becomes available. Alternatively, consider a "puzzle solving contract":

Finally, the first part of the contract, namely the phrase "Transfer bonus in record ..." could also be fairly arbitrary. Instead of transferring "bonuses" around we could just as well transfer arbitrary tokens of value:

The value and importance of such arbitrary tokens will, of course, be determined by how they are perceived by the community using the corresponding blockchain. It is not unreasonable to envision situations where being DA BOSS gives certain rights in the society, and having this fact recorded in an automatically-verifiable public record ledger makes it possible to include the this knowledge in various automated systems (e.g. consider a door lock which would only open to whoever is currently known as DA BOSS in the blockchain).

Honest Computing

As you see, we can use a distributed blockchain to keep journals, transfer "coins" and implement "smart contracts". These three applications are, however, all consequences of one general, core property. The participants of a distributed blockchain ("assistants" in the Alice example above, or "miners" in Bitcoin-speak) are motivated to precisely follow all rules necessary for confirming the blocks. If the rules say that a valid block is the one where all signatures and hashes are correct, the miners will make sure these indeed are. If the rules say that a valid block is the one where a contract function needs to be executed exactly as specified, the miners will make sure it is the case, etc. They all seek to get their confirmation bonuses, and they will only get them if they participate in building the longest honestly computed chain of blocks.

Because of that, we can envision blockchain designs where a "block confirmation" requires running arbitrary computational algorithms, provided by the users, and the greedy miners will still execute them exactly as stated. This general idea lies behind the Ethereum blockchain project.

There is just one place in the description provided above, where miners have some motivational freedom to not be perfectly honest. It is the decision about which records to include in the next block to be confirmed (or which algorithms to execute, if we consider the Ethereum blockchain). Nothing really prevents a miner to refuse to ever confirm a record "John is DA BOSS", ignoring it as if it never existed at all. This problem is overcome in modern blockchains by having users offer additional "tip money" reward for each record included in the confirmed block (or for every algorithmic step executed on the Ethereum blockchain). This aligns the motivation of the network towards maximizing the number of records included, making sure none is lost or ignored. Even if some miners had something against John being DA BOSS, there would probably be enough other participants who would not turn down the opportunity of getting an additional tip.

Consequently, the whole system is economically incentivised to follow the protocol, and the term "honest computing" seems appropriate to me.

Steganography is a marvelous subject, which could be considered a subfield of cryptography. Unfortunately, it is some-why absolutely underrated nowadays. It is not covered by the standard computer science curricula (although it would fit perfectly both within lectures on Cryptography as well as Signal Processing), and way too many people believe steganography is something akin to adding grey stamps to images in Photoshop. Even the almighty Wikipedia, in its corresponding article, does not provide a decently clear view of the field, in my opinion. To fix this I thought I'd give a try at making up a short explanation myself.

As mentioned, steganography is somewhat of a fellow discipline to cryptography. While the goal of cryptography is to protect the communication channel between Alice and Bob from some hypothetical evil Eve, the goal of steganography is to conceal the fact of communication itself. The classical setting is described as follows: Alice and Bob are kept imprisoned by the evil warden Walter. They are allowed to talk to each other, but Walter is listening to everything. How could Alice and Bob arrange a prison break without raising suspicion?

Steganographic problems

More specifically, steganographic problems can be divided into steganography against a passive warden, and steganography against an active warden.

Passive warden steganography

In this case Walter can only observe Alice and Bob's communication, but may not interfere. Walter's task is to be able to detect which of the messages between Alice and Bob contain secret meanings (if they do). If Walter comes up with a method by which he can distinguish innocent messages from the ones with a secret meaning with nontrivial probability, we shall say that Walter has succeeded in a "passive attack" on Alice and Bob's steganographic system.

Besides helping imaginary prisoners hide from imaginary wardens, passive steganography has many practical applications. For example, some printers add a barely visible watermark to each printed page, which identifies the printer model and the date. Radio and TV advertisers sometimes include in their clips a hidden identifier of the product being advertised (which simplifies automated airtime monitoring and validation). Storage of image metainfo within the image itself (e.g. storing the patient id within its X-ray picture) may prevent confusion when data is transferred or converted, etc.

It must be noted, that from the perspective of classical cryptography the methods mentioned above are not very interesting. Indeed, it is customary to assume in cryptography that all the details of the protocol used between Alice and Bob are open to all parties, including Walter. The only thing that Walter should not know is the "key". Without knowing this key Walter should be incapable of attacking the system. This is not the case in the examples with the printers and advertisements. No keys are involved and anyone who knows the algorithm can immediately discover the hidden message (i.e. attack the system).

The methods for designing such systems focus primarily on techniques for adding information to a known audio/video/textual signal without distorting it in a perceivable manner and, possibly, making the presence of this information resilient to transformations that the signal may pass (video streaming, file format conversion, text normalization, etc). Consequently, the complexity of many such methods lies mostly in the area of signal processing. In the case of audio, for example, it could mean finding sound frequency components that, on one hand, will be left unchanged by most audio codecs, yet on the other hand could be modified without the listener perceiving the change. In some sense it resembles a fight between the codec (which attempts to remove any redundant channels) and the steganographic system (which aims to make use of any redundancy remaining).

Active warden steganography

A more interesting situation is where Walter is not only listening in to Alice and Bob's communications, but may also actively interfere, removing any potential hidden meanings. The best example here is copyright protection. They say that movies, when shown in cinemas, would usually contain a steganographic watermark in their video signal, which identifies the particular movie theatre. The "warden" here is a movie pirate, who might know about the existence of the watermark, and would be interested in removing it (without corrupting the movie itself, of course). Consequently, the watermark must be included in a way, where Walter the pirate is incapable of removing it, even if he knew all the details of the watermarking algorithm (except for a secret key, of course). Besides movie watermarking, similar techniques could be used by other authors to "sign" their creations so that their authorship could later be established, when necessary.

Methods

Multiple methods exist for solving both the active and passive warden steganography. Not being able to list all of them, I will mention just the two core concepts, which I think are enough for an introductory overview.

LSB-steganography

The most well-known example of steganography - least-significant-bit (LSB) steganography - is applicable to analog data, such as music and images. The idea is that small changes in some values (pixels, frequency components) of an analog signal would not affect the perception of the signal in a notable way. For example, by tuning some pixels in an image one could transmit several bits of additional information. Of course, the choice of those pixels should be determined using a shared secret key, otherwise Walter could easily detect or remove the covert message.

The problem in the most naive version of this approach is that not every pixel in an image can be safely modified. For example, in regions filled with a single color any such change will be easy to spot. This can be overcome by only picking the pixels with enough variability in their neighborhood. Another weakness of the method is that the steganogram may be easy to remove by resizing or cropping the image. This can be prevented by hiding information in the spectral components rather than pixels - those are more resistant to the usual transformations. In fact, if we are dealing with a photograph or anything else that will be saved as a JPEG file, this approach would be quite nontrivial to break. The same ideas are used for steganographic processing of audio and video signals as well.

Equivalence-class steganography

Quite often Alice has a choice for multiple options for sending the same message. For example, when writing a text message to Bob, she can choose the phrasings. She can write "Hi" instead of "Hello", "Robert" instead of "Bob", punctuation can be used in multiple ways, and so on. When Alice is writing a novel, she is free to choose the names of the characters and places, chapter titles and even the order of events. Knowing the possible equivalence classes for the messages to be sent (e.g. words or sentences) as well as a common key, Alice may easily choose her words so that only Bob would be able to grasp whether there is a secret meaning and, if so, what it is.

A simple practical example of a coding algorithm is the following: Alice will code a single bit by each sentence of her text. For obtaining this bit, Bob will have to apply a hash function to the sentence plus the secret key and use the last bit of that hash. During coding Alice will simply have to choose words so that each sentence would correspond to a correct bit.

In its bare form the method is easy to attack - Walter may try to rephrase the text himself on transmission. This, in turn, can be overcome if Alice would hide the bits only into particularly chosen words or word sets (which can only be found by knowing the key), and do it using redundant coding (thus Walter would need to significantly alter the text if he wanted to be sure the message is removed). If Alice hides the message into the names of the characters of her novel, Walter may have no chances at all.

Methods like that are claimed to be used by large software companies to watermark their code (here, instead of choosing synonymous words a specific algorithm will be choosing synonymous bytecode instructions). This makes it possible to track the particular license which was used to leak a pirated version. Another example is geographic mapping software, which may use various equivalent ways of displaying a fractal shore in order to watermark the image.

As noted, other approaches and techniques exist (I did not find the space to properly mention public key steganography here, for example), yet I belive that LSB and EC-steganography largely illustrate the core ideas behind modern steganography in general as well as its possibilities and limitations. For those interested in the security proofs behind such techniques, this paper is a must read.

Playing cards are a great tool for modeling, popularizing and explaining various mathematical and algorithmic notions. Indeed, a deck of cards is a straightforward example for a finite set, a discrete distribution or a character string. Shuffling and dealing cards represents random sampling operations. A card hand denotes information possessed by a party. Turning card face down or face up looks a lot like bit flipping. Finally, card game rules describe an instance of a particular algorithm or a protocol. I am pretty sure that for most concepts in maths or computer science you can find some card game or a card trick that is directly related to it. Here are some examples of how you can simulate a simple computing machine, illustrate inductive reasoning or explain map-reduce, in particular.

Cryptographers seem to be especially keen towards playing cards. Some cryptographic primitives could have been inspired by them. There are decently secure ciphers built upon a deck of cards. Finally, there are a couple of very enlightening card-based illustrations of such nontrivial cryptographic concepts as zero-knowledge proofs and voting protocols. The recent course on secure two-party computation given by abhi shelat at the last week's EWSCS extended my personal collection of such illustrations with another awesome example — a secure two-party protocol for computing the AND function. As I could not find a description of this protocol anywhere in the internet (and abhi did not know who is the author), I thought it was worth being written up in a blog post here (along with a small modification of my own).

The Tinder Game

Consider the situation, where Alice and Bob want to find out, whether they are both interested in each other (just as if they were both users of the Tinder app). More formally, suppose that Alice has her private opinion about Bob represented as a single bit (where "0" means "not interested" and "1" means "interested"). Equivalently, Bob has his private opinion about Alice represented in the same way. They need to find out whether both bits are "1". However, if it is not the case, they would like to keep their opinions private. For example, if Alice is not interested in Bob, Bob would prefer Alice not to know that he is all over her. Because, you know, opinion asymmetry may lead to awkward social dynamics when disclosed, at least among college students.

The following simple card game happens to solve their problem. Take five cards, so that three of them are red and two are black. The cards of one color must be indistinguishable from each other (e.g. you can't simply take three different diamonds for the reds). Deal one black and one red card to Alice, one black and one red card to Bob. Put the remaining red card on the table face up.

Initial table configuration

Now Alice will put her two cards face down to the left of the open card, and Bob will put his two cards to the right of the open card:

Alice and Bob played

The rules for Alice and Bob are simple: if you like the other person, put your red card next to the central red card. Otherwise, put your black card next to the central one. For example, if both Alice and Bob like each other, they would play their cards as follows (albeit still face down):

What Alice and Bob would play if they both liked each other

Now the middle card is also turned face down, and all five cards are collected, preserving their order:

Five cards collected, preserving order

Next, Alice cuts this five-card deck, moving some number of cards from the top to the bottom (Bob should not know exactly how many). Then Bob cuts the deck (also making sure that Alice does not know how many cards he cuts). The result is equivalent to applying some cyclic rotation to the five card sequence yet neither Bob nor Alice knows how many cards were shifted in total.

The five cards can now be opened by dealing them in order onto the table to find out the result. If there happen to be three red cards one after another in a row or two black cards one after another, Alice and Bob both voted "yes". Here is one example of such a situation. It is easy to see that it is a cyclic shift of the configuration with three red aces in the middle shown above.

Both voted "yes"

Otherwise, if neither three red aces nor two black aces are side by side, we may conclude that one or both of the players voted "no". However, there is absolutely no way to find out anything more specific than that. Here is an example:

No mutual affection (or no affection at all)

Obviously, this result could not be obtained as a cyclic shift of the configuration with three aces clumped together. On the other hand, it could have been obtained as a cyclic shift from any of the three other alternatives ("yes-no", "no-no" and "no-yes"), hence if Alice voted "no" she will have no way of figuring out what was Bob's vote. Thus, playing cards along with a cryptographic mindset helped Alice and Bob discover their mutual affection or the lack of it without the risk of awkward situations. Isn't it great?

Throwing in a Zero-Knowledge Proof

There are various ways Alice or Bob can try to "break" this protocol while still trying to claim honesty. One possible example is shown below:

Alice is trying to cheat

Do you see what happened? Alice has put her ace upside down, which will later allow her to understand what was Bob's move (yet she can easily pretend that turning a card upside down was an honest mistake). Although the problem is easily solved by picking a deck with asymmetric backs, for the sake of example, let us assume that such a solution is somewhy unsuitable. Perhaps there are no requisite decks at Alice and Bob's disposal, or they need to have symmetric backs for some other reasons. This offers a nice possibility for us to practice even more playing card cryptography and try to secure the original algorithm from such "attacks" using a small imitation of a zero-knowledge proof for turn correctness.

Try solving it yourself before proceeding.

Read more...

Bitcoin is a cryptographic currency, that has gained a lot of hype in the last year. From a technical perspective, it is simply a distributed timestamping scheme, fully dedicated to establishing the order of monetary transactions, by creating a long block chain.

Adding a new block to the block chain requires extremely expensive distributed computations. Thus, in terms of the amount of energy, invested by the users worldwide into its creation, the block chain is, at the moment, probably the most expensive computer-generated file in human history. A monument to the raw "computation for the sake of computation". The Bitcoin network by now includes hundreds of thousands of users, most of whom keep a full copy of the block chain and contribute to its further growth.

Timestamping hash, published in a paper

All that means that including any information into the block chain can act as a solid timestamp, proving the existence of this information at a particular point in time. It is nearly impossible to fake or revoke. Even if the Bitcoin network would cease working, the block chain would probably be kept around at least as a curious artifact (as well as an object of interest for data miners) . The idea is equivalent to a popular practice of timestamping information by publishing it in a widely distributed newspaper. However, publishing in a popular newspaper may be costly, while getting transactions into the block chain is nearly free and accessible to anyone.

Consequently, it seems obvious that sooner or later the bitcoin block chain must begin to be used for timestamping things other than transactions. Because trusted timestamping is a big deal. Everyone in Estonia knows that.

Unfortunately, it seems that although the idea has been mentioned before, there do not seem to be any convenient services developed for that, apart from BTProof, which is somewhat too simplistic, given the potential importance of the task at hand. In an attempt to perhaps inspire someone to consider imlementing a more serious service of this kind, let me give a brief overview of the ways to get your data into the block chain.

Smuggling your data into the block chain

If only Bitcoin transactions were allowed to have textual descriptions assigned to them, the task would be trivial: any piece of information you want to timestamp could be simply mentioned in the description of a transaction. However, this functionality is not part of the Bitcoin protocol, so we have to use tricks. At least three different techniques are possible here.

1.  Specifying your data as a destination address.

Each Bitcoin transaction includes a "destination address", which is a 34-character string in hex-like encoding. This address may be specified arbitrarily. Thus, by transferring any amount to an address, which itself is the hash of the information you need timestamped, you will have the fact of information's existence mentioned in the block chain for future generations to behold. This is the idea behind BTProof. There are several problems with this method. Most importantly, anything you transfer to a nonexistent address will get lost forever, with no one being able to claim it. This makes the process non-free, because you cannot have transactions of size 0. Moreover, very small transactions are unfavoured by the Bitcoin network and take a long time to get verified. Finally, leaving "unclaimed" transactions forever hanging in the block chain is somewhat indecent in the first place, isn't it?

The abovementioned drawbacks may be addressed using multi-signature transactions. Those are a special type of transactions, which allow the funds to be claimed by any one of several addresses. In this case one address can be used to encode the hash and another one — to reclaim the funds spent in the transaction back. This concept has been suggested as the way to carry arbitrary data on top of Bitcoin in the MasterCoin project.

2. Specifying your data as a destination private key.

Rather than converting the data you need timestamped into a (non-existent) address, you can turn it into a private key. You can then perform two transactions. The first one  transfers funds to an address, corresponding to this private key, and next one uses the private key to withdraw the funds back to you. As there is a fixed mapping from your data to the private key to the address that the funds went through, you have just included a trace of your data into the block chain. This method is mentioned here. The drawback is the need for two transactions, and the overall complexity of the scheme.

3. Specifying your data in the script.

Finally, the last two places in a bitcoin transaction, which allow custom data, are the two "script" fields. Namely, the act of depositing funds to a transaction in Bitcoin is not as simple as providing the target address. Instead, it is a script, that, when executed, is supposed to check the right of the receiver to obtain the funds. Similarly, the act of withdrawing funds from Bitcoin is expressed by a script that proves the rights of the owner.

For example, a typical "deposition script" looks as follows:

OP_DUP 
OP_HASH160
OP_PUSHDATAx <target_address>
OP_EQUALVERIFY
OP_CHECKSIG

This script means that in order to withdraw the funds, the receiver must push on the stack a signature of the transaction, followed by his public key. The script then starts executing by first duplicating (OP_DUP) the top value on the stack, the public key. It then applies a hash function (OP_HASH160) to the top value on the stack (this converts the public key to an address). Then another value is pushed onto the stack (OP_PUSHDATAx). Next, two top values are popped and checked for equality (OP_EQUALVERIFY). This verifies, that the receiver's address matches <target_address>. Finally, the OP_CHECKSIG command pops another two values from the stack (those are the signature and the public key now, remember), and verifies the correctness of the signature.

The beauty of the system is that it lets you create various rules for claiming funds apart from simply owning a private key to an address. For example, it is possible to create transactions which require multiple parties to collude to withdraw them. Or you may require the receiver of the funds to solve a puzzle. Or you may even put the funds up for anyone to take freely, etc.

What is important for our purposes, however, is that the scripting language is rather flexible. In particular, it lets you add useless commands, such as "push this data onto stack, then drop the top value from stack, then continue as normal:"

OP_PUSHDATAx <any_data> 
OP_DROP 
OP_HASH160
OP_PUSHDATAx <target_address>
OP_EQUALVERIFY
OP_CHECKSIG

This logic could be included in either the "depositing" or the "receiving" script, letting you essentially provide arbitrary "notes" in transactions and thus do timestamp data in the most reasonable way. This lets you timestamp using a single transaction, which recurrently transfers any amount from an address to itself.

Unfortunately, it seems that the freedom of scripting has been severely limited in the recent versions of Bitcoin software. Namely, transactions with any nonstandard scripts are simply declined from inclusion into a block (at least, none of my attempts to try this out succeeded). Even the fate of multi-signature transactions, mentioned in point 1 (which are just a particular kind of a script) is not completely clear. In any case, the Bitcoin specification will most probably evolve to eventually allow storing dedicated data packets in the block chain without the need to resort to hacks. And if not Bitcoin, perhaps such functionality will become part of one of the competing similar cryptocurrencies.

It seems unreasonable to run a huge distributed timestamping algorithm, and not let people use it for general-purpose timestamping, doesn't it?

Update: Given the recent problems related to the transaction malleability aspect of the protocol, it is easy to predict that the freedom of scripting will probably be limited even further in the future. However, eventually support must be added for storing a custom nonce into the signed transaction (as it seems to be the only reasonable way to make transactions uniquely identifiable despite malleability of their hash). That nonce would be a perfect candidate for general-purpose timestamping purposes.