Four Years Remaining

Symbols and Reality

Mathematics is a language. An abstract set of generic symbols for describing concepts, objects and systems. Take, for example, the symbol "5", "five". What is it? Is it a real-world object? No. It is just a symbol. You are free to attach to it any interpretation that you deem appropriate. Of course, most of the times you would use the common interpretation of "5" as a natural number, denoting, well, "five of something". Literally meaning that you can count something as "this, this, this, this and this".

Take a moment to reflect on the degree of generality of this simple concept, "five". It can be applied to practically anything. Five apples, five centimeters, five centuries are notions as different from each other as you could imagine, and yet all of them relate to the concept "five". On the other hand, it is not too generic to be useless: "five" is radically different from "six", "seven", and an infinity of other numbers. This kind of magical balance between generality and specificity is common to mathematics. This is what makes mathematics both widely applicable and yet still incredibly useful.

Besides just giving us symbols like 5 or 6, mathematics provides an endless variety of ways for expressing "rules", "operations", "statements", "derivations", "computations" and the like, such as 5+5=10, or , etc. Once again, all of these rules, operations and statements need not necessarily bear any relation with reality. After all, they all are just a cunning play with symbols. And yet, quite often they do describe reality incredibly well. I know that 512 apples and 512 apples will make 1024 apples together. How do I know it? Certainly not because I checked it on real apples! I just believe that the real-world operation of "adding apples" can be satisfactory modeled using the formal symbolic framework of natural numbers and the operation of addition on them. Why do I believe it? This is a tricky philosophical question that we shall leave aside for now. But remember that any application of mathematics to the real world is always based on a belief that the chosen model describes the world well.

The Nature of Uncertainty

There are often cases where we would like to use mathematics to model "uncertainty". Now remember that from the point of view of pure math there are no such things as inherent "certainty" and "uncertainty". Mathematics will always operate on symbols and use precise, uniquely reproducible transformation rules between these symbols. Yet there are often cases when we, in our interpretations of these symbols, would like refer to certain entities as "uncertain". The reasons can be various:

1. Sometimes, we would like to use a single generalized concept to summarize multiple objects.
   - What is the height of a human?
   There is no single clear answer and yet it is possible to provide one using an uncertainty model such as a probability distribution.
2. Sometimes, we want to reason about some single numeric value which, even if it were well-defined, we just could not compute exactly.
   - What is the AVERAGE height of a human?
   In theory, it is a number you could measure by lining up all the people in the world and computing their average, but it is certainly an infeasible project.
3. Sometimes, the notion we would like to reason about is inherently not well-defined.
   - What is MY height, after all?
   The answer depends on a number of factors such as time, measuring equipment, my precise posture, etc. Instead of taking all of these into consideration, we prefer to exploit an uncertainty model.
4. Sometimes we just need a single concept to encapsulate a state of knowledge more sophisticated than pure numeric equality. For example, to express the fact like "my height IS GREATER THAN 150cm" without using the "greater than" operation.

There are also other situations, which are difficult to classify, but in all cases the idea is the same — for one reason or another we "don't know" (or "don't specify") the exact single quantity we want to reason about, an yet we still "know something" about it. In fact, amusingly, the amount of information that we use to represent an "uncertain" quantity is often much greater than the amount of information we would need to represent a "certain" one. For example, there are much more probability distributions than there are real numbers. Therefore, picking one probability distribution to represent our knowledge of a number is, in principle, a more informative step than picking a single real number. And yet, we call the former case "uncertainty" and the latter one "certainty". Because that's how we choose to name and interpret things, that's how we believe these concepts relate to reality.

Models of Uncertainty

The adjective "uncertain" is something you could, in theory, apply generically to any type of data. In a computer scientist's terms, it makes perfect sense to talk about datatypes "uncertain int", "uncertain real", "uncertain boolean", "uncertain string", "uncertain graph", "uncertain map" and maybe even "uncertain uncertain real" and the like. Let's limit ourselves here to the consideration of uncertain numbers only, as these are the most commonly used and well-studied types of uncertainty. So how do you model (or, say, "implement") "uncertain real"? Here is a short list of the most popular options:

1. Approximate numbers.Although you might not consider it as a smart approach, this is probably the most common choice in practice — using a usual number to represent an uncertain one. In this case the uncertainty is purely interpretative: instead of stating 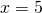you would, perhaps, write 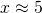, denoting your state of ignorance. Quite often you would not even care to use the approximate equality sign, presuming it is clear from the context that you are not supposed to provide an ideally exact measurement: — What is your height? — It is 180cm. This works quite well in simple real-life situations, such as buying a kilogram of apples or discussing the horsepowers in a friend's motorbike, but is also applicable to some more technical cases, such as computing the distance to the nearest star.The advantage of such implied uncertainty is that you do not really need to deal with it. All of your familiar arithmetic operations come for free, together with their well established interpretations and the nice properties, theories and theorems. The disadvantage is that once your data is approximate, all of these theories and theorems become approximate too. So, although it could often be acceptable to claim 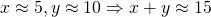, you would have problems explaining more complicated steps, such as " 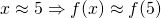for a continuous f".But what to do if you need to perform such steps? Consider intervals instead!
2. Intervals.The second most popular method of representing an uncertain real number is to provide an interval where it falls into. It is ubiquitous in engineering disciplines. Most often an interval is expressed either as 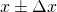or by following the significant figures convention (e.g. writing 180.00 to denote 180±0.01). It is an improvement over the previous approach, because now you have a way to quantify the effect of function application on uncertainty. For example, a commonly used rule would be

   ,

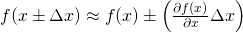   where f is a differentiable function.

3. Sets.An approach slightly more general than the "interval" technique would be to provide a set of values, to which the value of interest could belong to. So, instead of stating x = 5 you could write, for example, .This allows for more mathematical rigour. For example: 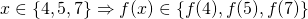. Moreover, besides the standard algebraic operations, the set representation allows to update the knowledge about an uncertain value easily using set unions and intersections:

   .

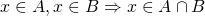   However, sets are "heavy" object to work with, so you don't see this approach being used too often in practical computations. Some Monte-Carlo simulations would use a set to represent approximate solutions, but they would convert it to a probability distribution as soon as possible. This leads us to the next item on the list.

4. Probability distributions.If the previous methods were either too crude, too ad-hoc or too heavy, then probability theory was designed to provide flexible balance and help overcome most of their drawbacks. To represent a number it suggests us to use a probability measure - an additive function that assigns a weight to each set, which could contain the value of interest. The greater the weight of a set - the more probable it is that the value belongs to that set. By convention, the minimum possible weight of a set is 0, which we usually interpret as "the value almost certainly does not belong to that set", and the maximum weight is 1, with a corresponding interpretation "the value almost certainly belongs there". Representing a function defined on sets is complicated, so usually we use a simpler equivalent representation: a cumulative distribution function (CDF) or a probability density function (PDF). The plot of the latter is especially insightful and provides a nice visual cue about the nature of uncertainty being modeled.It is impossible to enumerate all the virtues of using a probability distribution as an uncertainty model. A probability distribution is a flexible structure, capable of accomodating most "common" kinds of uncertainty. There is an authoritative, well-developed theory and a wide range of both practical and theoretical tools available. Besides the standard algebraic operations, you have rules for updating knowledge (such as the Bayes rule) and a range of facilities for decision making (estimation, hypothesis testing, etc). Finally, there are various interpretations available for you to choose from.Of course, there are potential drawbacks, too. On the practical side, it is not always computationally convenient to work with a probability measure. It is a function, after all, and when specified arbitrarily it can either take too much space to represent or too much time to compute. The use of smoothing and approximation techniques can somewhat relieve the problem, but comes at the price of additional assumptions and simplifications. Secondly, a probability distribution is not capable of representing any kind of uncertainty: for example, there is no probability distribution corresponding to the statement "x < 5". Thirdly, the requirement for a probability density to be normalized to sum to 1 is sometimes inconvenient (because you have to normalize) or unintuitive (because it seems to declare that there is a single uncertain value "hidden inside").

   

   For example, consider the picture on the right and try to provide a concise description of the set of black pixels on it. This will be an uncertain notion because, well, a gray pixel is also somewhat black, isn't it? And although you could provide a probability distribution of "black" on the picture, you would probably intuitively prefer to assign a "truth-value" between 0 and 1 to each pixel, with 1 corresponding to "certainly black" and 0 to "certainly not black". This would, however, violate the "sum-to-one" normalization rule and thus would not be a probability density. What would it be? A fuzzy set.

5. Fuzzy sets.A fuzzy set is a set whose elements can have a degree of membership between 0 and 1. It is therefore something inbetween a set (because it "feels" like a set) and a probability density (because it is a function, only this time normalized to have a maximum of 1, instead of the integral of 1). A person familiar with probability theory will also easily recognize a straightforward analogy of a fuzzy set to a likelihood function.Fuzzy sets seem to be a natural uncertainty model in various circumstances, such as the "black pixels" example above. They are often conceptually simpler to specify than probability densities, and lack the interpretation controversy surrounding probability theory. On the other hand, the theory of fuzzy sets is not as extensive as that of probabilities. It is rich in operations like max and min, which makes some things computationally difficult. Besides, the lack of a universal interpretation for fuzzy membership values results in a lack of simple unique decision-making facilities. There are just way too many defuzzification rules to choose from.
6. ... and more.A variety of other approaches is available, the most important ones being Possibility theory, and Dempster-Shafer theory. However, as this text has already grown too long for a blog post, I shall leave the detailed description of these to Wikipedia.

Summary

The main message of this exposition is actually quite simple. There are various approaches to modeling uncertainty. They differ in the type of supported operations and, most importantly, in the way we interpret them and map to the real world entities. But nonetheless, these are all still just methods for modeling uncertainty, each with its own advantages and limitations. Moreover, in most situations, as long as you use the math "reasonably", the models are approximately equivalent in terms of the results and decisions you might end up with using them. That is probably the reason why practitioners would rarely consider anything more sophisticated than a probability measure (except, perhaps, when they are feeling adventurous). And that is why it can sometimes be complicated to promote the more "modern" approaches without the awkward looks from the side of the "traditional statistics". After all, these approaches are competing on the same field with The One and Only, Probability Theory.

Imagine that you have just derived a novel IQ test. You have established that for a given person the test produces a normally-distributed unbiased estimate of her IQ with variance 10². That is, if, for example, a person has true IQ=120, the test will result in a value from a N(120,10²) distribution. Also, from your previous experiments you know that among all the people, IQ has a N(110,15²) distribution.

One a sunny Monday morning you went out on a street and requested the first bypasser (whose name turned out to be John) to take your test. The resulting score was t=125. The question is: what can you conclude now about the true IQ of that person (assuming, of course, that there is such a thing as a "true IQ"). There are at least two reasonable approaches to this problem.

1. You could apply the method of maximum likelihood. Here's John, standing beside you, and you know his true IQ must be some real number a. The test produced an unbiased estimate of a equal to 125. The likelihood of the data (i.e. the probability of obtaining a test score of 125 for a given a) is therefore:

      

   The maximum likelihood method suggests picking the value of a that maximizes the above expression. Finding the maximum is rather easy here and it turns out to be at a=125, which is pretty natural. You thus conclude that the best what you can say about John's true IQ is that it is approximately 125.

2. An alternative way of thinking is to use the method of maximum a-posteriori probability, where instead of maximizing likelihood , you maximize the a-posteriori probability . The corresponding expression is:

   

   Finding the required maximum is easy again, and the solution turns out to be a=120.38. Therefore, by this logic, John's IQ should be considered to be somewhat lower than what the test indicates.

Which of the two approaches is better? It might seem utterly unbelievable, but the estimate provided by the second method is, in fact, closer to the truth. The straightforward "125", proposed to by the first method is biased, in the sense that on average this estimate is slightly exaggerated. Think how especially unintuitive this result is from the point of view of John himself. Clearly, his own "true IQ" is something fixed. Why on Earth should he consider "other people" and take into account the overall IQ distribution just to interpret his own result obtained from an unbiased test?

To finally confuse things, let us say that John got unhappy with the result and returned to you to perform a second test. Although it is probably impossible to perform any real IQ test twice and get independent results, let us imagine that your test can indeed be repeated. The second test, again, resulted in a score of 125. What IQ estimate would you suggest now? On one hand, John himself came to you and this time you could regard his IQ as a "real" constant, right? But on the other hand, John is just a person randomly picked from the street, who happened to take your test twice. Go figure.

PS: Some additional remarks are appropriate here:

• Although I'm not a fan of The Great Frequentist-Bayesian War, I cannot but note that the answer is probably easier if John is a Bayesian at heart, because in this case it is natural for him to regard "unknown constants" as probability distributions and consider prior information in making inferences.
• If it is hard for you to accept the logic in the presented situation (as it is for me), some reflection on the similar, but less complicated false positive paradox might help to relieve your mind.
• In general, the correct way to obtain the true unbiased estimate is to compute the mean over the posterior distribution:

     

  In our case, however, the posterior is symmetric and therefore the mean coincides with the maximum. Computing the mean by direct integration would be much more complicated.

Consider the following excerpt from a recent article in the British Medical Journal:

Mike has only two children, and they are called Pat and Alex, which could equally be boys’ or girls’ names. In fact, Pat is a girl. What is the probability that Alex is a boy?

a 50%
b Slightly less than 50%
c Slightly more than 50%
d Between 60% and 70%
e Between 40% and 30%

d—Although this could be about the relative popularity of ambiguous names for boys and girls or about subtle imbalances in the sex ratio, it is not meant to be. The clue to the correct answer is in thinking about what we do not know about the family and what we do know already, and applying this to the expected probabilities of girls and boys.

We do not know if Pat was born first or second. We do know that there are only two children and that Pat is a girl. I am assuming that in the population, 50% of children are girls.

The birth order and relative frequency of two child families are: boy, boy (25%), girl, girl (25%), boy, girl (25%) girl, boy (25%). We know Mike’s family does not have two boys, since Pat is a girl, so we are only left with three choices for families with at least one girl. Two of these pairs have a boy and one does not. Hence the probability that Alex is a boy is two thirds or 66.7%.

If we had been told that Pat was born first then the probability that Alex is a boy drops to 50%.

The well-known "Boy or Girl" paradox that is referenced in the fragment above is probably as old as the probability theory itself. And it is therefore quite amusing to see an incorrect explanation for it presented in a serious journal article. You are welcome to figure out the mistake yourself.

For completeness sake, here is my favourite way of presenting this puzzle:

In the following, let Mike be a randomly chosen father of two kids.

1. Mike has two kids, one of them is a boy. What is the probability that the other one is a girl?
2. Mike has two kids, the elder one is a boy. What is the probability that the other one is a girl?
3. Mike has two kids. One of them is a boy named John. What is the probability that the other one is a girl?
4. I came to visit Mike. One of his two kids, a boy, opened the door to me. What is the probability that Mike's other child is a girl?
5. I have a brother. What is the probability that I am a girl?
6. I have a brother named John. What is the probability that I am a girl?

You can assume that boys and girls are equiprobable, the births of two kids are independent events, a randomly chosen boy will be named John with probability p, and that a family may have two kids with the same name.

If you haven't tried solving these yet, give it a try. I'm pretty sure you won't do all 6 questions correctly on the first shot.

It is good to attend lectures from time to time, even if these are on the topics that you "already know". Because, once in a while, you get to find out something new about things that are so "simple" and "familiar", that you thought there was nothing new you could possibly discover about them. So, today I've had an accidental revelation regarding a simple yet amusing property of the maximum likelihood estimation method. I think I should have been told that years ago, right on the first statistics course.

Maximum Likelihood

Maximum likelihood estimation is one of the simplest and most popular methods for fitting mathematical models to given data. It is most easily illustrated by an example. Suppose you are given a list of numbers , which, you believe, are all instances of a normally distributed random variable with mean and variance . The problem is that the value of is unknown to you and you would like to estimate it from the data. How do you do it? The maximum likelihood method suggests you to search for a value of , for which the probability (or probability density) of obtaining exactly this set of numbers would be maximal. That is:

In most cases this turns out to be quite a reasonable suggestion, which leads to good estimates (although, there are some rare exceptions). Here, for example, it turns out that to estimate the mean you should simply compute the average of the given numbers:

This is more-or-less all what a typical textbook has to say about maximal likelihood, but there's more to it.

Counting Lightbulbs

Consider the following example. Suppose you are willing to measure the average lifetime of a common lightbulb (that is, the amount of time it will glow until burning out). For that you buy 1000 lightbulbs in a general store, switch all of them on and wait for a year, keeping track of the timepoints at which the  individual lightbulbs burn out. Suppose the year has passed and you managed to record the lifetime of just 50 "dead" lightbulbs (the remaining 950 keep on glowing even after the whole year of uninterrupted work). What do you do now? Do you wait for other lightbulbs to burn out? But this can take ages! Do you just discard the 950 lightbulbs and only consider the 50 for which you have "available data"? This is also not good, because, clearly, the knowledge that 95% of lightbulbs live longer than a year is important. Indeed, from this fact alone you could infer that the average lifetime must be between 18 and 21 years with 95% confidence (an interested reader is invited to verify this claim). So what do you do?

Assume that the lifetime of a lightbulb can be modeled using exponential distribution with mean (this is a natural assumption because exponential distribution is well-suited for describing the lifetime of electric equipment). Then the probability (probability density, in fact) that lightbulb i burns out after years can be expressed as:

.

Naturally, the likelihood of lightbulbs 1,2,3,...,50 burning out after years correspondingly, is just the product of the corresponding expressions:

.

Now what about the lightbulbs that are still alive? The likelihood that a lightbulb will glow longer than a year can be easily expressed as:

.

Therefore, the total likelihood of having 50 lightbulbs burn out at time moments and 950 lightbulbs keep working longer than a year is the following product:

.

Finding the estimate of that maximizes this expression is now a simple technical detail of minor importance. What is important is the ease with which we managed to operate the "uncertain measurements" for the 950 lightbulbs.

Final Remarks

Note that the idea can be extended to nearly arbitrary kinds of uncertainty. For example, if, for some lightbulb we knew that its lifetime was a number between a and b, we would include this piece of knowledge by using the term in the likelihood function. This inherent flexibility of the maximum likelihood method looks like a feature quite useful for the analysis of noisy data.

Surprisingly, however, it does not seem to be applied much in practice. The reason for that could lie in the fact that many nontrivial constraints on the data will make the likelihood function highly nonconvex and hard to optimize. Consider, for example, the probability density

for a normally distributed variable X. Depending on the choice of , , and , the likelihood function will have either three different peaks at , two peaks or just one. Thus, finding an exact optimum is much harder than in the typical textbook case. But on the other hand, there are various cases where the likelihood function is nicely convex (consider the interval constraint mentioned above) and besides there are numerous less efficient algorithms around anyway. So maybe the trick is not used much, simply because it's not in the textbook?

Probability theory is often used as a sound mathematical foundation to formalize and derive solutions to the real-life problems in fields such as game theory, decision theory or theoretical economics. However, it often turns out that the somewhat simplistic "traditional" probabilistic approach is insufficient to formalize the real world, and this results in a large number of rather curious paradoxes.

One of my favourite examples is the Ellsberg's paradox, which goes as follows. Imagine that you are presented with an urn, containing 3 white balls and 5 other balls, that can be gray or black (but you don't know how many of these 5 exactly are gray, and how many are black). You will now draw one ball from the urn at random, and you have to choose between one of the two gambles:

1A)

You win if you draw a white ball.

1B)

You win if you draw a black ball.

Which one would you prefer to play? Next, imagine the same urn with the same balls, but the following choice of gambles:

2A)

You win if you draw either a white or a gray ball.

2B)

You win if you draw either a black or a gray ball.

The paradox lies in the fact, that most people would strictly prefer 1A to 1B, and 2B to 2A, which seems illogical. Indeed, let the number of white balls be W=3, the number of gray balls be G and the number of black balls - B. If you prefer 1A to 1B, you seem to be presuming that W > B. But then W+G > B+G and you should necessarily also be preferring 2A to 2B.

What is the problem here? Of course, the problem lies in the uncertainty behind the number of black balls. We know absolutely nothing about it, and we have to guess. Putting it in Bayesian terms, in order to make a decision we have specify our prior belief in what is the probability that there would be 0, 1, 2, 3, 4 or 5 black balls in the urn. The classical way of modeling the "complete uncertainty" would be to state that all the options are equiprobable. In this case the probability of having more black balls in the urn than the white balls is only 2/6 (this can happen when there are 4 or 5 black balls, each option having probability 1/6), and it is therefore reasonable to bet on the whites. We should therefore prefer 1A to 1B and 2A to 2B.

The real life, however, demonstrates that the above logic does not adequately describe how most people decide in practice. The reason is that we would not assign equal probabilities to the presumed number of black balls in the urn. Moreover, in the two situations our prior beliefs would differ, and there is a good reason for that.

If the whole game were real, there would be someone who had proposed it to us in the first place. This someone was also responsible for the number of black balls in the urn. If we knew who this person was, we could base our prior belief on our knowledge of that person's motives and character traits. Is he a kindhearted person who wants us to win, or is he an evil adversary who would do everything to make us lose? In our situation we don't know, and we have to guess. Would it be natural to presume the uncertainty to be a kindhearted friend? No, for at least the following reasons:

• If the initiator of the game is not a complete idiot, he would aim at gaining something from it, or why would he arrange the game in the first place?
• If we bet on the kindness of the opponent we can lose a lot when mistaken. If, on the contrary, we presume the opponent to be evil rather than kind, we are choosing a more robust solution: it will also work fine for the kind opponent.

Therefore, it is natural to regard any such game as being played against an adversary and skew our prior beliefs to the safer, more robust side. The statement of the problem does not clearly require the adversary to select the same number of black balls for the two situations. Thus, depending on the setting, the safe side may be different. Now it becomes clear why in the first case it is reasonable to presume that the number of black balls is probably less than the number of white balls: this is the only way the adversary can make our life more difficult. In the second case, the adversary would prefer the contrary: a larger number of black balls. Therefore, we would be better off reversing our preferences. This, it seems to me, explains the above paradox and also nicely illustrates how the popular way of modeling total uncertainty using a uniform prior irrespective of the context fails to consider the real-life common sense biases.

The somewhat strange issue remains, however. If you now rephrase the original problem more precisely and define that the number of black balls is uniformly distributed, many people will still intuitively tend to prefer 2B over 2A. One reason for that is philosophical: we might believe that the game with a uniform prior on the black balls is so unrealistic, that we shall never really have the chance to take a decision in such a setting. Thus, there is nothing wrong in providing a "wrong" answer for this case, and it is still reasonable to prefer the "wrong" decision because in practice it is more robust. Secondly, I think most people never really grasp the notion of true uniform randomness. Intuitively, the odds are always against us.

Appendix

There are still a pair of subtleties behind the Ellsberg's problem, which might be of limited interest to you, but I find the discussion somewhat incomplete without them. Read on if really want to get bored.

Namely, what if we especially stress, that you have to play both games, and both of them from the same urn? Note that in this case the paradox is not that obvious any more: you will probably think twice before betting on white and black simultaneously. In fact, you'd probably base your decision on whether you wish to win at least one or rather both of the games. Secondly, what if we say that you play both games simultaneously by picking just one ball? This would provide an additional twist, as we shall see in a moment.

I. Two independent games

So first of all, consider the setting where you have one urn, and you play two games by drawing two balls with replacement. Consider two goals: winning at least one of the two games, and winning both.

I-a) Winning at least one game

To undestand the problem we compute the probabilities of winning game 1A, 1B, 2A, 2B for different numbers of black balls, and then the probabilities of winning at least one of two games for our different choices:

Now the problem can be regarded as a classical game between us and "the odds": we want to maximize our probabilities by choosing the gamble correctly, and "the odds" wants to minimize our chances by providing us with a bad number of black balls. The game presented above has no Nash equilibrium, but it seems that the choice of 3 black balls is the worst for us on average. And if we follow this pessimistic assumption, we see that the correct choice would be to pick consistently either both "A" or both "B" gambles (a further look suggests that both "A"-s is probably the better choice of the two).

I-b) Winning two games
Next, assume that we really need to win both of the games. The following table summarizes our options:

This game actually has a Nash equilibrium, realized when we select options 1A and 2B. Remarkably, it corresponds exactly to the claim of the paradox: when we need to win both games and are pessimistic about the odds, we should prefer the options with the least amount of uncertainty.

II. Two dependent games
Finally, what if both games are played simultaneously by taking just one ball from the urn. In this case we also have two versions: aiming to win at least one, or aiming to win both games.

II-a) Winning at least one game
The solution here is to choose either the 1A-2B or the 1B-2A version, which always guarantees exactly one win. Indeed, if you pick a white ball, you win 1A, and otherwise you win 2B. The game matrix is the following:

II-b) Winning both games
The game matrix looks as follows:

The situation here is contrary to the previous: if you win 1A, you necessarily lose 2B, so here you have to bet both "A"-s to achieve a Nash equilibrium.

Summary
If you managed to read to this point, then I hope you've got the main idea, but let me summarize it once more: the main "problem" with the Ellsberg's paradox (as well as a number of other similar paradoxes) can be in part due to the fact that pure "uniform-prior" probability theory is not the correct way to approach game-theoretical problems, as it tends to hide from view a number of aspects that we, as humans, usually handle nearly subconsciously.