Four Years Remaining

Early stopping is a technique that is very often used when training neural networks, as well as with some other iterative machine learning algorithms. The idea is quite intuitive - let us measure the performance of our model on a separate validation dataset during the training iterations. We may then observe that, despite constant score improvements on the training data, the model's performance on the validation dataset would only improve during the first stage of training, reach an optimum at some point and then turn to getting worse with further iterations.

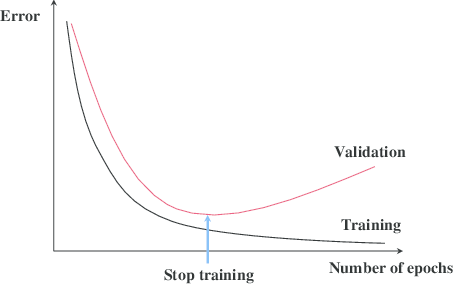
The early stopping principle

It thus seems reasonable to stop training at the point when the minimal validation error is achieved. Training the model any further only leads to overfitting. Right? The reasoning sounds solid and, indeed, early stopping is often claimed to improve generalization in practice. Most people seem to take the benefit of the technique for granted. In this post I would like to introduce some skepticism into this view or at least illustrate that things are not necessarily as obvious as they may seem from the diagram with the two lines above.

How does Early Stopping Work?

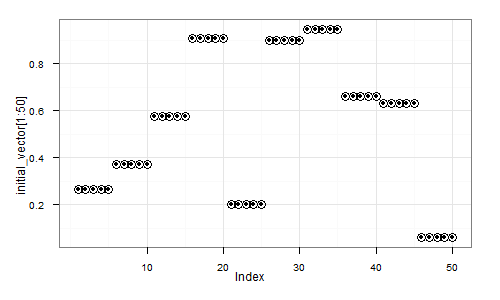
To get a better feeling of what early stopping actually does, let us examine its application to a very simple "machine learning model" - the estimation of the mean. Namely, suppose we are given a sample of 50 points from a normal distribution with unit covariance and we need to estimate the mean of this distribution.

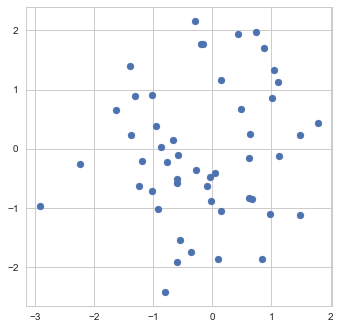
Sample

The maximum likelihood estimate of can be found as the point which has the smallest sum of squared distances to all the points in the sample. In other words, "model fitting" boils down to finding the minimum of the following objective function:

As our estimate is based on a finite sample, it, of course, won't necessarily be exactly equal to the true mean of the distribution, which I chose in this particular example to be exactly (0,0):

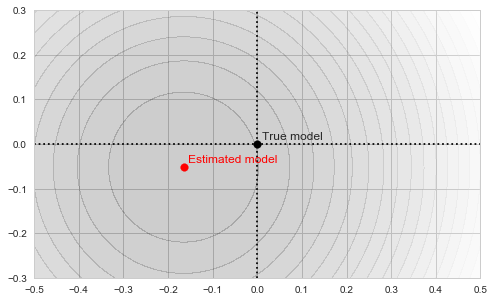
Sample mean as a minimum of the objective function

The circles in the illustration above are the contours of the objective function, which, as you might guess, is a paraboloid bowl. The red dot marks its bottom and is thus the solution to our optimization problem, i.e. the estimate of the mean we are looking for. We may find this solution in various ways. For example, a natural closed-form analytical solution is simply the mean of the training set. For our purposes, however, we will be using the gradient descent iterative optimization algorithm. It is also quite straightforward: start with any point (we'll pick (-0.5, 0) for concreteness' sake) and descend in small steps downwards until we reach the bottom of the bowl:

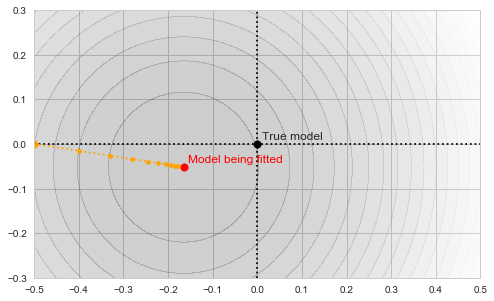
Gradient descent

Let us now introduce early stopping into the fitting process. We will split our 50 points randomly into two separate sets: 40 points will be used to fit the model and 10 will form the early stopping validation set. Thus, technically, we now have two different objective functions to deal with:

and

Each of those defines its own "paraboloid bowl", both slightly different from the original one (because those are different subsets of data):

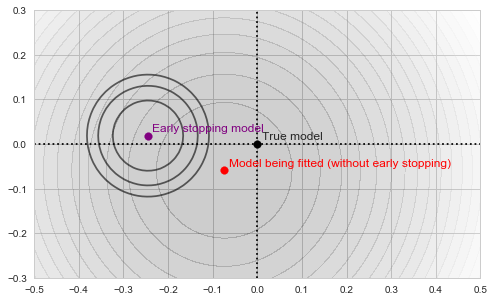
Fitting and early stopping objectives

As our algorithm descends towards the red point, we will be tracking the value of at each step along the way:

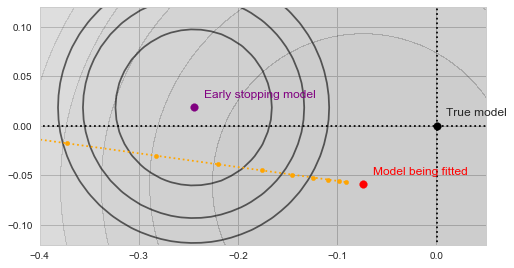
Gradient descent with validation

With a bit of imagination you should see on the image above, how the validation error decreases as the yellow trajectory approaches the purple dot and then starts to increase after some point midway. The spot where the validation error achieves the minimum (and thus the result of the early stopping algorithm) is shown by the green dot on the figure below:

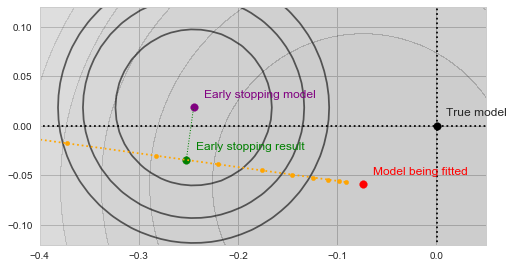
Early stopping

In a sense, the validation function now acts as a kind of a "guardian", preventing the optimization from converging towards the bottom of our main objective. The algorithm is forced to settle on a model, which is neither an optimum of nor of . Moreover, both  and use less data than , and are thus inherently a worse representation of the problem altogether.

So, by applying early stopping we effectively reduced our training set size, used an even less reliable dataset to abort training, and settled on a solution which is not an optimum of anything at all. Sounds rather stupid, doesn't it?

Indeed, observe the distribution of the estimates found with (blue) and without (red) early stopping in repeated experiments (each time with a new random dataset):

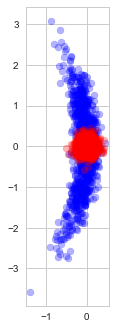
Solutions found with and without early stopping

As we see, early stopping greatly increases the variance of the estimate and adds a small bias towards our optimization starting point.

Finally, let us see how the quality of the fit depends on the size of the validation set:

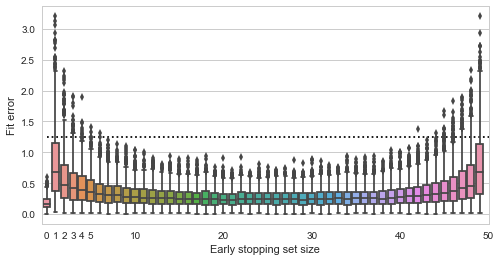
Fit quality vs validation set size

Here the y axis shows the squared distance of the estimated point to the true value (0,0), smaller is better (the dashed line is the expected distance of a randomly picked point from the data).  The x axis shows all possible sizes of the validation set. We see that using no early stopping at all (x=0) results in the best expected fit. If we do decide to use early stopping, then for best results we should split the data approximately equally into training and validation sets. Interestingly, there do not seem to be much difference in whether we pick 30%, 50% or 70% of data for the validation set - the validation set seems to play just as much role in the final estimate as the training data.

Early Stopping with Non-convex Objectives

The experiment above seems to demonstrate that early stopping should be almost certainly useless (if not harmful) for fitting simple convex models. However, it is never used with such models in practice. Instead, it is most often applied to the training of multilayer neural networks. Could it be the case that the method somehow becomes useful when the objective is highly non-convex? Let us run a small experiment, measuring the benefits of early stopping for fitting a convolutional neural-network on the MNIST dataset. For simplicity, I took the standard example from the Keras codebase, and modified it slightly. Here is the result we get when training the the most basic model:

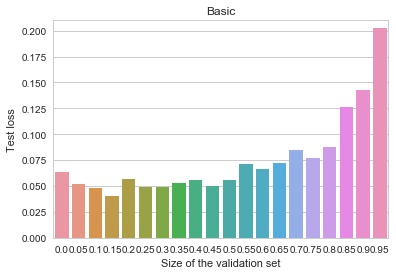
MNIST - Basic

The y axis depicts log-loss on the 10k MNIST test set, the x axis shows the proportion of the 60k MNIST training set set aside for early stopping. Ignoring small random measurement noise, we may observe that using early stopping with about 10% of the training data does seem to convey a benefit. Thus, contrary to our previous primitive example, when the objective is complex, early stopping does work as a regularization method. Why and how does it work here? Here's one intuition I find believable (there are alternative possible explanations and measurements, none of which I find too convincing or clear, though): stopping the training early prevents the algorithm from walking too far away from the initial parameter values. This limits the overall space of models and is vaguely analogous to suppressing the norm of the parameter vector. In other words, early stopping resembles an ad-hoc version of  regularization.

Indeed, observe how the use of early stopping affects the results of fitting the same model with a small -penalty added to the objective:

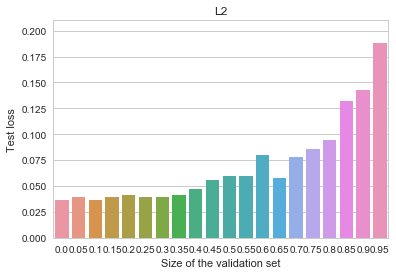
MNIST - L2

All of the benefits of early stopping are gone now, and the baseline (non-early-stopped, -regularized) model is actually better overall than it was before. Let us now try an even more heavily regularized model by adding dropout (instead of the penalty), as is customary for deep neural networks. We can observe an even cleaner result:

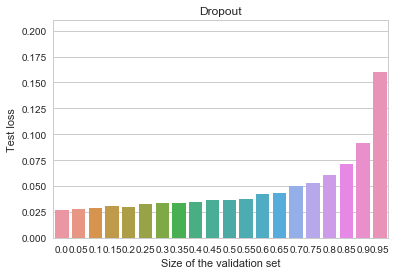
MNIST - Dropout

Early stopping is again not useful at all, and the overall model is better than all of our previous attempts.

Conclusion: Do We Need Early Stopping?

Given the reasoning and the anecdotal experimental evidence above, I personally tend to think that beliefs in the usefulness of early stopping (in the context of neural network training) may be well overrated. Even if it may improve generalization for some nonlinear models, you would most probably achieve the same effect more reliably using other regularization techniques, such as dropout or a simple penalty.

Note, though, that there is a difference between early stopping in the context of neural networks and, say, boosting models. In the latter case early stopping is actually more explicitly limiting the complexity of the final model and, I suspect, might have a much more meaningful effect. At least we can't directly carry over the experimental examples and results in this blog post to that case.

Also note, that no matter whether early stopping helps or harms the generalization of the trained model, it is still a useful heuristic as to when to stop a lengthy training process automatically if we simply need results that are good enough.

Collecting large amounts of data and then using it to "teach" computers to automatically recognize patterns is pretty much standard practice nowadays. It seems that, given enough data and the right methods, computers can get quite precise at detecting or predicting nearly anything, whether it is face recognition, fraud detection or movie recommendations.

Whenever a new classification system is created, it is taken for granted that the system should be as precise as possible. Of course, classifiers that never make mistakes are rare, but if it possible, we should strive to have them make as few mistakes as possible, right? Here is a fun example, where things are not as obvious.

Consider a bank, which, as is normal for a bank, makes money by giving loans to its customers. Of course, there is always a risk that a customer will default (i.e. not repay the loan). To account for that, the bank has a risk scoring system which, for a given loan application, assesses the probability that the corresponding customer may default. This probability is later used to compute the interest rate offered for the customer. To simplify a bit, the issued interest on a loan might be computed as the sum of customer's predicted default risk probability and a fixed profit margin. For example, if a customer is expected to default with probability 10% and the bank wants 5% profit on its loans on average, the loan might be issued at slightly above 15% interest. This would cover both the expected losses due to non-repayments as well as the profit margin.

Now, suppose the bank managed to develop a perfect scoring algorithm. That is, each application gets a rating of either having 0% or 100% risk. Suppose as well that within a month the bank processes 1000 applications, half of which are predicted to be perfectly good, and half - perfectly bad. This means that 500 loans get issued with a 5% interest rate, while 500 do not get issued at all.

Think what would happen, if the system would not do such a great job and confused 50 of the bad applications with the good ones? In this case 450 applications would be classified as "100%" risk, while 550 would be assigned a risk score of "9.1%" (we still require the system to provide valid risk probability estimates). In this case the bank would issue a total of 550 loans at 15%. Of course, 50 of those would not get repaid, yet this loss would be covered from the increased interest paid by the honest lenders. The financial returns are thus exactly the same as with the perfect classifier. However, the bank now has more clients. More applications were signed, and more contract fees were received.

True, the clients might be a bit less happy for getting a higher interest rate, but assuming they were ready to pay it anyway, the bank does not care. In fact, the bank would be more than happy to segment its customers by offering higher interest rates to low-risk customers anyway. It cannot do it openly, though. The established practices usually constrain banks to make use of "reasonable" scorecards and offer better interest rates to low-risk customers.

Hence, at least in this particular example, a "worse" classifier is in fact better for business. Perfect precision is not really the ultimately desired feature. Instead, the system is much more useful when it provides a relevant and "smooth" distribution of predicted risk scores, making sure the scores themselves are decently precise estimates for the probability of a default.

When it comes to data analysis, there are hundreds of exciting approaches: simple summary statistics and hypothesis tests, various clustering methods, linear and nonlinear regression or classification techniques, neural networks of various types and depths, decision rules and frequent itemsets, feature extractors and dimension reductors, ensemble methods, bayesian approaches and graphical models, logic-based approaches and fuzzy stuff, ant colonies, genetic algorithms and other optimization methods, monte-carlo algorithms, sampling and density estimation, logic-based and graph methods. Don't even get me started on the numerous visualization techniques.

This sheer number of options is, however, both a blessing and a curse at the same time. In many practical situations just having those methods at your disposal may pose more problems than solutions. First you need to pick one of the approaches that might possibly fit your purpose. Then you will try to adapt it appropriately, spend several iterations torturing the data only to obtain very dubious first results, come to the conclusion that most probably you are doing something wrong, reconvince yourself that you need to try harder in that direction, spend some more iterations testing various parameter settings. Nothing works as you want it to, so you start everything from scratch with another method to find yourself obtaining new, even more dubious results, torturing the data even further, getting tired of that and finally settling on something "intermediately decent", which "probably makes sense", although you are not so sure any more and feel frustrated.

I guess life of a statistician was probably way simpler back in the days when you could run a couple of t-tests, or an F-test from a linear regression and call it a day. In fact, it seems that many experimental (e.g. wetlab) scientists still live in that kind of world, when it comes to analyzing their experimental results. The world of T-tests is cozy and safe. They don't get you frustrated. Unfortunately, t-tests can feel ad-hockish, because they force you to believe that something "is normally distributed". Also, in practice, they are mainly used to confirm the obvious rather than discover something new from the data. A simple scatterplot will most often be better than a t-test as an analysis method. Hence, I am not a big fan of T-tests. However, I do have my own favourite statistical method, which always feels cozy and safe, and never gets me frustrated. I tend to apply it whenever I see a chance. It is the Fisher exact test in the particular context of feature selection.

My appreciation of it stems from my background in bioinformatics and some experience with motif detection in particular. Suppose you have measured the DNA sequences for a bunch of genes. What can you do to learn something new about the sequence structure from that data? One of your best bets is to first group your sequences according to some known criteria. Suppose you know from previous experiments that some of the genes are cancer-related whereas others are not. As soon as you have specified those groups, you can start making observations like the following: "It seems that 10 out of my 20 cancer-related genes have the subsequence GATGAG in their DNA code. The same sequence is present in only 5 out of 100 non-cancer-related ones. How probable would it be to obtain similar counts of GATGAG, if the two groups were picked randomly?" If the probability to get those counts at random is very low, then obviously there is something fishy about GATGAG and cancer - perhaps they are related. To compute this probability you will need to use the hypergeometric distribution, and the resulting test (i.e. the question "how probable is this situation in a random split?") is known as the Fishers' exact test.

This simple logic (with a small addition of a multiple testing correction on top) has worked wonders for finding actually important short sequences on the DNA. Of course it is not limited to sequence search. One of our research group's most popular web tools uses the same approach to discover functional annotations, that are "significantly overrepresented" in a given group of genes. The same approach can be used to construct decision trees, and in pretty much any other "supervised learning" situation, where you have groups of objects and want to find binary features of those objects, associated with the groups.

Although in general the Fisher test is just one particular measure of association, it is, as I noted above, rather "cozy and comfortable". It does not force me to make any weird assumptions, there is no "ad-hoc" aspect to it, it is simple to compute and, most importantly, in my experience it nearly always produces "relevant" results.

Words overrepresented in the speeches of Greece MPs

A week ago me, Ilya and Alex happened to take part in a small data analysis hackathon, dedicated to the analysis of speech transcripts from the European Parliament. Somewhat analogously to DNA sequences, speeches can be grouped in various ways: you can group them by the speaker who gave them, by country, gender or political party of that speaker, by the month or year when the speech was given or by any combination of such groupings. The obvious "features" of a speech are words, which can be either present or not present in it. Once you view the problem this way the task of finding group-specific words becomes self-evident and the Fisher test is the natural solution to it. We implemented this idea and extracted "country-specific" and "time-specific" words from the speeches (other options were left out due to time constraints). As is usual the case with my favourite method, the obtained results look relevant, informative and, when shown in the form of a word cloud, fun. Check them out.

The complete source code of the analysis scripts and the visualization application is available on Github.

This is a repost of my quora answer to the question: In layman's terms, how does Naive Bayes work?

Suppose that you are a working as a security guard at the airport. Your task is to look at people who pass the security line and pick some of them as being worthy of a more detailed screening. Now, of course, telling whether a person is a potential criminal or not by just looking at him/her is hard, if at all possible, but you need to do something. You have been put there for some reason, after all.

One of the simplest ways to approach the problem, mentally, is the following. You assign a "risk value" for each person. At the beginning (when you don't have any information about the person at all) you set this value to zero.

Now you start studying various features of the person in front of you: is it a male or a female? Is it a kid? Is he behaving nervously? Is he carrying a big bag? Is he alone? Did the metal detector beep? Is he a foreigner? etc. For each of those features you know (subconsciously due to your presuppositions, or from actual statistics) the average increase or decrease in risk of the person being a criminal that it entails. For example, if you know that the proportion of males among criminals is the same as the proportion of males among non-criminals, observing that a person is male will not affect his risk value at all. If, however, there are more males among criminals (suppose the percentage is, say, 70%) than among decent people (where the proportion is around 50%), observing that a person in front of you is a male will increase the "risk level" by some amount (the value is log(70%/50%) ~ 0.3, to be precise). Then you see that a person is nervous. OK, you think, 90% of criminals are nervous, but only 50% of normal people are. This means that nervousness should entail a further risk increase (of log(0.9/0.5) ~ 0.6, to be technical again, so by now you have counted a total risk value of 0.9). Then you notice it is a kid. Wow, there is only 1% of kids among criminals, but around 10% among normal people. Therefore, the risk value change due to this observation will be negative (log(0.01/0.10) ~ -2.3, so your totals are around -1.4 by now).

You can continue this as long as you want, including more and more features, each of which will modify your total risk value by either increasing it (if you know this particular feature is more representative of a criminal) or decreasing (if the features is more representative of a decent person). When you are done collecting the features, all is left for you is to compare the result with some threshold level. Say, if the total risk value exceeds 10, you declare the person in front of you to be potentially dangerous and take it into a detailed screening.

The benefit of such an approach is that it is rather intuitive and simple to compute. The drawback is that it does not take the cross-play of features into account. It may very well be the case that while the feature "the person is a kid" on its own greatly reduces the risk value, and the feature "has a moustache" on its own has close to no effect, a combination of the two ("a kid with a moustache") would actually have to increase the risk by a lot. This would not happen when you simply add the separate feature contributions, as described above.

It is annoying how popular it is to ignore the Y-axis limits on bar charts nowadays. Unfortunately, this is also the default mode for most plotting packages, so no one wants to do anything about it. But something must be done.

Visualization is a very powerful method for data analysis. Very often, plotting a bunch of scatterplots, barplots, heatmaps, animations or other kinds of imagery is enough to immediately see by your own eyes, whether there are any interesting patterns in the data (which often means you have nearly solved the problem) or not (which means you should prepare yourself for a long-term battle with the data which might not end up succesfully for you).

Visualization is powerful because by visualizing data you essentially "plug it" directly into your brain's processing engine, using the visual interface that happens to be supported by your brain. You need to convert the data into CSV or an XLS format to load it into Excel. Analogously, you need a 2d image or an animation to load the data into your brain - it is that simple.

This view suggests two immediate developments. Firstly, why don't we use the other "interfaces" that our brain has with the outside world for data processing? Could converting data to something which sounds, feels, tastes or smells be a useful method for exploiting our brain's analytic capabilities even further? Obviously, visual input has the most impact simply due to the fact that the retina is an immediate part of the brain. However, auditory signals, for example, seem to have a powerful processing system in our brain dedicated to them too.

Secondly, if we can appreciate how much our brain is capable of extracting from a single image, why don't we try to automate such an approach? Modern computer vision has reached sufficient maturity to be capable of extracting fairly complex informative features from images. This suggests that a particular 2d plot of a dataset can be used as a kind of an informative "data fingerprint" which, when processed by a computer vision-driven engine, could be analyzed on the presence of "visible" patterns and visual similarity to other datasets.

The fun part is that there has been some research done in this direction. Consider the paper "Computer Vision for Music Identification" by Yan Ke et al. The authors propose to convert pieces of music into a spectrogram image. Those spectrogram images can then be compared to each other using methods of computer vision, thus resulting in an efficient similarity metric, usable for search and identification of musical pieces. The authors claim to achieve 95% precision at 90% recall, which compares favourably to alternative methods. I think it would be exciting to see more of such techniques applied in a wider range of areas.

Representing audio as pictures, figure from (Y.Ke, 2005)

This post presumes you are familiar with PCA.

Consider the following experiment. First we generate a random vector (signal) as a sequence of random 5-element repeats. That is, something like

(0.5, 0.5, 0.5, 0.5, 0.5,   0.9, 0.9, 0,9, 0.9, 0,9,   0.2, 0.2, 0.2, 0.2, 0.2,   ... etc ... )

In R we could generate it like that:

num_steps = 50
step_length = 5;
initial_vector = c();
for (i in 1:num_steps) {
  initial_vector = c(initial_vector, rep(runif(1), step_length));
}

Here's a visual depiction of a possible resulting vector:

plot(initial_vector), zoomed in

Next, we shall create a dataset, where each element will be a randomly shifted copy of this vector:

library(magic) # Necessary for the shift() function
dataset = c()
for (i in 1:1000) {
  shift_by = floor(runif(1)*num_steps*step_length) # Pick a random shift
  new_instance = shift(initial_vector, shift_by)   # Generate a shifted instance
  dataset = rbind(dataset, new_instance);          # Append to data
}

Finally, let's apply Principal Component Analysis to this dataset:

pca = prcomp(dataset)

Question - how do the top principal components look like? Guess first, then read below for the correct answer.

Read more...

It is not uncommon when a long-running scientific study or an experiment produces results which are, at best, uninteresting. The measured effect may be too weak to be reported on convincingly given the data at hand. None the less, resources have been put into it, many man-months have been spent, and thus a paper must be published. The researcher must therefore present his results in a way convincing enough for the reviewers to be lulled into acceptance.

The following are the three best methods for doing that (and I have seen those being used in practice). Next time you read someone's paper (or write your own), keep them in mind.

1. Use an irrelevant (and preferably strict) hypothesis test.
   Suppose you want to show that a set of measurements in one group differs from the set of measurements in the other group. The typical approach here is the T-test or the Wilcoxon test, both of which detect whether elements in one group are on average greater than those in the other group. If, however, you find that the tests fail on your data (i.e., there is no easily detectable difference in measurement magnitudes), why don't you try something like the Kolmogorov-Smirnov test, which checks whether the distributions of the two groups are different. It is a much stricter condition. In fact the tiniest outlier in your data will easily get you a low p-value and thus something to stick in the face of a reviewer. If even the KS test did not work, try testing something even less relevant, such as, whether your data is normally distributed. Most probably it is not, here's your low p-value! Remember - the smaller your p-values, the better is your paper!
2. Avoid significance testing completely
   If you can't get a low p-value anywhere, do not worry. Significance testing is going somewhat out of fashion nowadays anyway, so it is possible to avoid it and still sound convincing. If one group of measurements has 40% of successes and the other has 42% - why not simply present those two numbers as obvious proof that the second group is better. Using ratios is also a smart idea. Say, some baseline algorithm has a 1% chance of success. You now test your algorithm and discover that out of 10 trials it had 1 success. That means your algorithm has just demonstrated a 10% success rate, which is ten times better than the baseline! Finally, ROC curves can often be used to hide the fact that your data is too tiny to make any conclusions. No one really ever checks for significance of those.
3. Sweep multiple testing under the carpet
   If you are analyzing a dataset with 1000 attributes and 50 datapoints, it is not really very surprising if one of those attributes will seem "interesting" (e.g. highly correlated with the target effect) purely by chance - there is often nothing significant in finding one out of a thousand. However, if you only mention that one (or perhaps 10-50) of the original attributes, your results will magically become significant and no reviewer will be able to catch your cheating.

There are certainly more, and I'll keep the post updated if I come up with a worthy addition. If you have something to add, please do comment.

I've recently stumbled upon a simple observation, which does not seem to be common knowledge and yet looks quite enlightening. Namely: polynomials provide an excellent way of modeling data in an order-agnostic manner.

The situations when you need to represent data in an order-agnostic way are actually fairly common.  Suppose that you are given a traditional sample and are faced with a task of devising a generic function of the sample, which could only depend on the values in the sample, but not on the ordering of these values. Alternatively, you might need to prove that a given statistic is constant with respect to all permutations of the sample. Finally, you might simply wish to have a convenient mapping for your feature vectors that would lose the ordering information, but nothing else.

The most common way of addressing this problem is sorting the sample and working with the order statistics  instead of the original values. This is not always convenient. Firstly, the mapping of the original sample to the corresponding vector of order statistics (i.e. the sorting operation) is quite complicated to express mathematically. Secondly, the condition that the vector of order statistics is always sorted is not very pleasant to work with. A much better idea is to represent your data as a polynomial of the form

This will immediately provide you with a marvellous tool: two polynomials and are equal if and only if their roots are equal, which means, in our case, that the samples and are equal up to a reordering.

Now in order to actually represent the polynomial we can either directly compute its coefficients

or calculate its values at any different points (e.g. at ) - in any case we end up with the same amount of data as we had originally (i.e. values), but the new representation is order-agnostic and has, arguably, much nicer properties than the order statistics vector.

It is not without its own problems, of course. Firstly, it requires at least time to compute. Secondly, not every polynomial will have real-valued roots. And thirdly, the interpretation of the new "feature vector" is not necessarily intuitive or meaningful. Yet nonetheless, it's a trick to consider.

The first step in the analysis of multivariate data is visualization. Histograms of attribute distributions, scatterplots, box-and-whiskers diagrams, parallel coordinate plots, self organizing maps, and even plots of happy faces - are all means of helping a human to visually comprehend multidimensional data and expoit the enormous power of the human brain to detect patterns. Of all these techniques, two-dimensional scatterplots are perhaps the most popular, as they tend to provide an especially "realistic" feel for the data. But when your data has more than two attributes (perhaps hundreds or thousands), how do you choose the two projection coordinates that would provide you with the "best angle" on the data?

The easiest answer to that question is, of course, to pick a pair of attributes A_i and A_j, and simply plot one versus the other. Unfortunately, this doesn't usually work well, especially when the dataset does have hundreds of attributes. Therefore, the most popular approach in practice is to use PCA and project the data onto the two largest principal components, which mostly results in a rather insightful image.

The PCA projection is, however, completely unsupervised. If your data has class labels assigned to points, PCA does not take them into account. No matter what is the labeling, PCA will always produce the same projection onto the coordinates with the highest variation. This might leave an improper impression that the two classes overlap a lot when in fact they do not. Therefore, this is not what you need. Usually, in the case of labeled data you expect from a scatterplot to provide an indication of how separated the two classes are from each other, and how difficult could it be to discriminate between them. It turns out that it is very easy to construct a linear projection with such properties.

The Linear classifier-based Scatterplot

Assume there are two classes in the data and we are interested in a linear projection, that demonstrates how separated the classes are. Let us train a linear classifier to discriminate the two classes. It does not matter which algorithm you use, as long as it results in a separating hyperplane. Now naturally, the normal to this hyperplane is the main coordinate of interest to you: it is the direction along which the data will be classified linearly by your algorithm. If there is a coordinate for demonstrating separation, this must be it. The choice of the second projection coordinate does not matter much, so I would propose picking any direction orthogonal to the first.

When you have three classes you could select the first projection coordinate as the normal of a hyperplane, separating the first class from the second, and the second coordinate as the normal of a hyperplane, separating the first class from the third.

Finally, note that in general you need not limit yourself to linear classifiers only. Any classifier of the form will provide you with an informative coordinate projection function . This is a natural "supervised" alternative to kernel-PCA or SOM.

Naive supervised linear scatterplot (NS-plot)

To be somewhat more specific, here's a suggestion of a very simple implementation for the abovementioned idea. To avoid the use of a potentially complicated linear classifier training algorithm, let us just pick the vector connecting the means of the two classes as the first projection coordinate. The second coordinate is chosen at random and then orthogonalized with the first one. The Scilab code of the whole algorithm is therefore the following:

  // Input:
  //   X - the data matrix (instances in rows, attributes in columns)
  //   C - class assignments (C(i) is the class of instance X(i,:))
  mean_1 = mean(X(C ==  1, :), 'r')';
  mean_2 = mean(X(C == -1, :), 'r')';
  v1 = (mean_2 - mean_1)/norm(mean_2 - mean_1);
  v2 = rand(v1);
  v2 = v2 - v2'*v1*v1;
  v2 = v2/norm(v2);
  X_proj = X*[v1 v2];
  // Output:
  //   X_proj - the projected coordinates

Notice how much simpler and more efficient it is than PCA. Despite the simplicity, I haven't seen the use of such a plot anywhere else, so let me coin the boring name NS-plot for it. Personal experience shows that the resulting plot is visually never much worse than a PCA plot, and most often the two plots complement each other. Let me illustrate that on two simple examples.

The IRIS dataset. The plots below show the PCA and the NS plots of the famous iris dataset (where I removed the first class). There is clearly no strong advantage of one plot over the other except that PCA is more difficult to compute.

The ARCENE dataset. The following plots depict the 1000-attribute ARCENE sample dataset. We can see how PCA prefers to stress the unsupervised clustering present in the dataset, thus potentially deemphasizing the specifics of class labeling. In this case, I would say, the PCA and the NS plots complement each other.

Bonus

Noticed the circled points on the plots above? This is one other small trick that I find quite useful, and that does not seem to be widely known. The circled points denote the "boundary" - these are the points whose nearest neighbor is of a different class than their own. The more boundary points there are - the more difficult is the classification problem. The boundary is not an absolute notion, because there are various ways to define distance between points. My suggestion would be to standardize all attributes and use the euclidean norm, unless you have good reasons to do something else (e.g. you a-priori know good weights for the attributes, etc).