The following is an expanded version of an explanatory comment I posted here.
Alice's Diary
Alice decided to keep a diary. For that she bought a notebook, and started filling it with lines like:
- Bought 5 apples.
- Called mom.
.... - Gave Bob $250.
- Kissed Carl.
- Ate a banana.
...
Alice did her best to keep a meticulous account of events, and whenever she had a discussion with friends about something that happened earlier, she would quickly resolve all arguments by taking out the notebook and demonstrating her records. One day she had a dispute with Bob about whether she lent him $250 earlier or not. Unfortunately, Alice did not have her notebook at hand at the time of the dispute, but she promised to bring it tomorrow to prove Bob owed her money.
Bob really did not want to return the money, so that night he got into Alice's house, found the notebook, found line 132 and carefully replaced it with "132. Kissed Dave". The next day, when Alice opened the notebook, she did not find any records about money being given to Bob, and had to apologize for making a mistake.
Alice's Blockchain
A year later Bob's conscience got to him and he confessed his crime to Alice. Alice forgave him, but decided to improve the way she kept the diary, to avoid the risk of forging records in the future. Here's what she came up with. The operating system Linups that she was using had a program named md5sum, which could convert any text to its hash - a strange sequence of 32 characters. Alice did not really understand what the program did with the text, it just seemed to produce a sufficiently random sequence. For example, if you entered "hello" into the program, it would output "b1946ac92492d2347c6235b4d2611184", and if you entered "hello " with a space at the end, the output would be "1a77a8341bddc4b45418f9c30e7102b4".
Alice scratched her head a bit and invented the following way of making record forging more complicated to people like Bob in the future: after each record she would insert the hash, obtained by feeding the md5sum program with the text of the record and the previous hash. The new diary now looked as follows:
- 0000 (the initial hash, let us limit ourselves with just four digits for brevity)
- Bought 5 apples.
- 4178 (the hash of "0000" and "Bought 5 apples")
- Called mom.
- 2314 (the hash of "4178" and "Called mom")
...
4492 - Gave Bob $250.
1010 (the hash of "4492" and "Gave Bob $250") - Kissed Carl.
8204 (the hash of "1010" and "Kissed Carl")
...
Now each record was "confirmed" by a hash. If someone wanted to change the line 132 to something else, they would have to change the corresponding hash (it would not be 1010 anymore). This, in turn, would affect the hash of line 133 (which would not be 8204 anymore), and so on all the way until the end of the diary. In order to change one record Bob would have to rewrite confirmation hashes for all the following diary records, which is fairly time-consuming. This way, hashes "chain" all records together, and what was before a simple journal became now a chain of records or "blocks" - a blockchain.
Proof-of-Work Blockchain
Time passed, Alice opened a bank. She still kept her diary, which now included serious banking records like "Gave out a loan" or "Accepted a deposit". Every record was accompanied with a hash to make forging harder. Everything was fine, until one day a guy named Carl took a loan of $1000000. The next night a team of twelve elite Chinese diary hackers (hired by Carl, of course) got into Alice's room, found the journal and substituted in it the line "143313. Gave out a $1000000 loan to Carl" with a new version: "143313. Gave out a $10 loan to Carl". They then quickly recomputed all the necessary hashes for the following records. For a dozen of hackers armed with calculators this did not take too long.
Fortunately, Alice saw one of the hackers retreating and understood what happened. She needed a more secure system. Her new idea was the following: let us append a number (called "nonce") in brackets to each record, and choose this number so that the confirmation hash for the record would always start with two zeroes. Because hashes are rather unpredictable, the only way to do it is to simply try out different nonce values until one of them results in a proper hash:
- 0000
- Bought 5 apples (22).
- 0042 (the hash of "0000" and "Bought 5 apples (22)")
- Called mom (14).
- 0089 (the hash of "0042" and "Called mom (14)")
...
0057 - Gave Bob $250 (33).
0001 - Kissed Carl (67).
0093 (the hash of "0001" and "Kissed Carl (67)")
...
To confirm each record one now needs to try, on average, about 50 different hashing operations for different nonce values, which makes it 50 times harder to add new records or forge them than previously. Hopefully even a team of hackers wouldn't manage in time. Because each confirmation now requires hard (and somewhat senseless) work, the resulting method is called a proof-of-work system.
Distributed Blockchain
Tired of having to search for matching nonces for every record, Alice hired five assistants to help her maintain the journal. Whenever a new record needed to be confirmed, the assistants would start to seek for a suitable nonce in parallel, until one of them completed the job. To motivate the assistants to work faster she allowed them to append the name of the person who found a valid nonce, and promised to give promotions to those who confirmed more records within a year. The journal now looked as follows:
- 0000
- Bought 5 apples (29, nonce found by Mary).
- 0013 (the hash of "0000" and "Bought 5 apples (29, nonce found by Mary)")
- Called mom (45, nonce found by Jack).
- 0089 (the hash of "0013" and "Called mom (45, nonce found by Jack)")
...
0068 - Gave Bob $250 (08, nonce found by Jack).
0028 - Kissed Carl (11, nonce found by Mary).
0041
...
A week before Christmas, two assistants came to Alice seeking for a Christmas bonus. Assistant Jack, showed a diary where he confirmed 140 records and Mary confirmed 130, while Mary showed a diary where she, reportedly, confirmed more records than Jack. Each of them was showing Alice a journal with all the valid hashes, but different entries! It turns out that ever since having found out about the promotion the two assistants were working hard to keep their own journals, such that all nonces would have their names. Since they had to maintain the journals individually they had to do all the work confirming records alone rather than splitting it among other assistants. This of course made them so busy that they eventually had to miss some important entries about Alice's bank loans.
Consequently, Jacks and Mary's "own journals" ended up being shorter than the "real journal", which was, luckily, correctly maintained by the three other assistants. Alice was disappointed, and, of course, did not give neither Jack nor Mary a promotion. "I will only give promotions to assistants who confirm the most records in the valid journal", she said. And the valid journal is the one with the most entries, of course, because the most work has been put into it!
After this rule has been established, the assistants had no more motivation to cheat by working on their own journal alone - a collective honest effort always produced a longer journal in the end. This rule allowed assistants to work from home and completely without supervision. Alice only needed to check that the journal had the correct hashes in the end when distributing promotions. This way, Alice's blockchain became a distributed blockchain.
Bitcoin
Jack happened to be much more effective finding nonces than Mary and eventually became a Senior Assistant to Alice. He did not need any more promotions. "Could you transfer some of the promotion credits you got from confirming records to me?", Mary asked him one day. "I will pay you $100 for each!". "Wow", Jack thought, "apparently all the confirmations I did still have some value for me now!". They spoke with Alice and invented the following way to make "record confirmation achievements" transferable between parties.
Whenever an assistant found a matching nonce, they would not simply write their own name to indicate who did it. Instead, they would write their public key. The agreement with Alice was that the corresponding confirmation bonus would belong to whoever owned the matching private key:
- 0000
- Bought 5 apples (92, confirmation bonus to PubKey61739).
- 0032 (the hash of "0000" and "Bought 5 apples (92, confirmation bonus to PubKey61739)")
- Called mom (52, confirmation bonus to PubKey55512).
- 0056 (the hash of "0032" and "Called mom (52, confirmation bonus to PubKey55512)")
...
0071 - Gave Bob $250 (22, confirmation bonus to PubKey61739).
0088 - Kissed Carl (40, confirmation bonus to PubKey55512).
0012
...
To transfer confirmation bonuses between parties a special type of record would be added to the same diary. The record would state which confirmation bonus had to be transferred to which new public key owner, and would be signed using the private key of the original confirmation owner to prove it was really his decision:
- 0071
- Gave Bob $250 (22, confirmation bonus to PubKey6669).
0088 - Kissed Carl (40, confirmation bonus to PubKey5551).
0012
...
0099 - TRANSFER BONUS IN RECORD 132 TO OWNER OF PubKey1111, SIGNED BY PrivKey6669. (83, confirmation bonus to PubKey4442).
0071
In this example, record 284 transfers bonus for confirming record 132 from whoever it belonged to before (the owner of private key 6669, presumably Jack in our example) to a new party - the owner of private key 1111 (who could be Mary, for example). As it is still a record, there is also a usual bonus for having confirmed it, which went to owner of private key 4442 (who could be John, Carl, Jack, Mary or whoever else - it does not matter here). In effect, record 284 currently describes two different bonuses - one due to transfer, and another for confirmation. These, if necessary, can be further transferred to different parties later using the same procedure.
Once this system was implemented, it turned out that Alice's assistants and all their friends started actively using the "confirmation bonuses" as a kind of an internal currency, transferring them between each other's public keys, even exchanging for goods and actual money. Note that to buy a "confirmation bonus" one does not need to be Alice's assistant nor register anywhere. One just needs to provide a public key.
This confirmation bonus trading activity became so prominent that Alice stopped using the diary for her own purposes, and eventually all the records in the diary would only be about "who transferred which confirmation bonus to whom". This idea of a distributed proof-of-work-based blockchain with transferable confirmation bonuses is known as the Bitcoin.
Smart Contracts
But wait, we are not done yet. Note how Bitcoin is born from the idea of recording "transfer claims", cryptographically signed by the corresponding private key, into a blockchain-based journal. There is no reason we have to limit ourselves to this particular cryptographic protocol. For example, we could just as well make the following records:
- Transfer bonus in record 132 to whoever can provide signatures, corresponding to PubKey1111 AND PubKey3123.
This would be an example of a collective deposit, which may only be extracted by a pair of collaborating parties. We could generalize further and consider conditions of the form:
- Transfer bonus in record 132 to whoever first provides
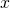 , such that
, such that 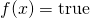 .
.
Here ![]() could be any predicate describing a "contract". For example, in Bitcoin the contract requires
could be any predicate describing a "contract". For example, in Bitcoin the contract requires ![]() to be a valid signature, corresponding to a given public key (or several keys). It is thus a "contract", verifying the knowledge of a certain secret (the private key). However,
to be a valid signature, corresponding to a given public key (or several keys). It is thus a "contract", verifying the knowledge of a certain secret (the private key). However, ![]() could just as well be something like:
could just as well be something like:
![]()
which would be a kind of a "future prediction" contract - it can only be evaluated in the future, once record 42000 becomes available. Alternatively, consider a "puzzle solving contract":
![]()
![]()
Finally, the first part of the contract, namely the phrase "Transfer bonus in record ..." could also be fairly arbitrary. Instead of transferring "bonuses" around we could just as well transfer arbitrary tokens of value:
- Whoever first provides
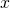 , such that
, such that 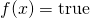 will be DA BOSS.
will be DA BOSS.
... 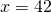 satisifes the condition in record 284.
satisifes the condition in record 284.
Now and forever, John is DA BOSS!
The value and importance of such arbitrary tokens will, of course, be determined by how they are perceived by the community using the corresponding blockchain. It is not unreasonable to envision situations where being DA BOSS gives certain rights in the society, and having this fact recorded in an automatically-verifiable public record ledger makes it possible to include the this knowledge in various automated systems (e.g. consider a door lock which would only open to whoever is currently known as DA BOSS in the blockchain).
Honest Computing
As you see, we can use a distributed blockchain to keep journals, transfer "coins" and implement "smart contracts". These three applications are, however, all consequences of one general, core property. The participants of a distributed blockchain ("assistants" in the Alice example above, or "miners" in Bitcoin-speak) are motivated to precisely follow all rules necessary for confirming the blocks. If the rules say that a valid block is the one where all signatures and hashes are correct, the miners will make sure these indeed are. If the rules say that a valid block is the one where a contract function needs to be executed exactly as specified, the miners will make sure it is the case, etc. They all seek to get their confirmation bonuses, and they will only get them if they participate in building the longest honestly computed chain of blocks.
Because of that, we can envision blockchain designs where a "block confirmation" requires running arbitrary computational algorithms, provided by the users, and the greedy miners will still execute them exactly as stated. This general idea lies behind the Ethereum blockchain project.
There is just one place in the description provided above, where miners have some motivational freedom to not be perfectly honest. It is the decision about which records to include in the next block to be confirmed (or which algorithms to execute, if we consider the Ethereum blockchain). Nothing really prevents a miner to refuse to ever confirm a record "John is DA BOSS", ignoring it as if it never existed at all. This problem is overcome in modern blockchains by having users offer additional "tip money" reward for each record included in the confirmed block (or for every algorithmic step executed on the Ethereum blockchain). This aligns the motivation of the network towards maximizing the number of records included, making sure none is lost or ignored. Even if some miners had something against John being DA BOSS, there would probably be enough other participants who would not turn down the opportunity of getting an additional tip.
Consequently, the whole system is economically incentivised to follow the protocol, and the term "honest computing" seems appropriate to me.







