Four Years Remaining

The Receiver Operating Characteristic Area Under the Curve (ROC AUC) is a measure of classifier performance, which is widely used in machine learning. Unfortunately, the obscure way the concept is explained in most sources makes it fairly hard to grasp its intuitive meaning. The name "area under the curve" itself is ill-conceived and is utterly useless in helping the intution. The aim of this post is to aid those struggling with the concept, and also present a simple and intuitive interpretation of the ROC AUC metric as the "average positive rank" which I, so far, have not seen stated explicitly elsewhere.

To facilitate explanation, let us consider a hypothetical classification problem: classifying chocolate bars to "very good" or "just OK" (hereby we presume a chocolate bar may not be considered "bad" by definition of chocolate). Suppose we have a sample of particular chocolate bar types, for which we have carefully assigned the proper classification, e.g.:

where class label "1" denotes "very good" and "0" means "just OK". Suppose we have derived a classifier which, based on some features of a chocolate bar, such as its chocolate content, packaging, country of origin, etc, attempts to assign a "goodness score" which should resemble our notion of goodness. For concreteness' sake, let us say the classifier assigned the following scores:

How do we assess the goodness of such a classifier? The "ROC approach" suggests we do the following. First, we shall plot a ROC curve. To do that, we order the chocolate bars according to their assigned score (this is already done in the table above) and use this ordering to write out the vector of the class labels (the "sorted prediction vector"):

Obviously, the best possible classifier would order the instances so that all the ones would be on the left of all the zeroes. The particular classifier we chose here looks good, but not perfect.

Next, we use the obtained vector to plot the ROC curve. To do this plot, forget all of the "True Positive Rate" and "False Positive Rate" nonsense you might have read about in most textbooks, and follow the following simple recipe:

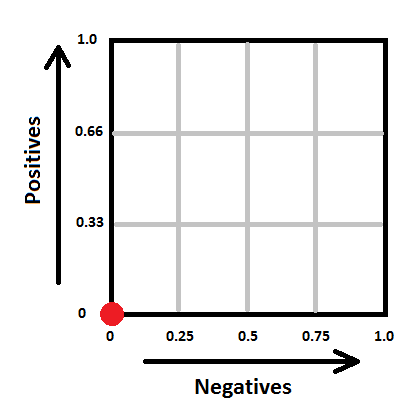
1. Draw a square with sides of length 1. Denote its its lower left corner as the "origin", its horizontal axis as "the negatives" and its vertical axis as "the positives". Split the negatives axis in as many parts as there are examples of class "0" in the dataset. Split the positives axis in as many parts as there are examples of class "1" in your dataset. In our case, the square will look as follows:
   

   The ROC square

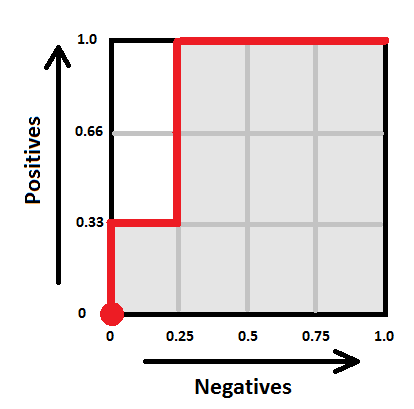
2. Next, take the sorted prediction vector, and draw a path, starting from the origin. For each "1" in the sorted prediction vector, the path will move one step "up", and for each "0" in the vector, the path will move one step "right" (note that if you have multiple predictions with the same score, make all the corresponding "up" and "right" moves at once by drawing the corresponding diagonal). In our case, the path goes ("up", "right", "up", "up", "right", "right", "right") and hence looks as follows:
   

   ROC curve

Voilà, this is your ROC curve. Obviously, the "perfect" classifier would make all the "up" steps first and the "right" steps last, hence the ideal ROC curve looks like a perfect corner. A random classifier would mix his "up" and "right" steps randomly, and the curve would most probably follow a diagonal-ish path. The one-number summary of the "goodness" of such a path is the "area under the curve" (coloured gray here), which will be 1.0 for the ideal case, and somewhere around 0.5 for the worst case. In our case the area is 10/12 ~ 0.83.

Here comes the important question — what does this number actually mean? One good answer is given by the following probabilistic interpretation:

The area under ROC curve specifies the probability that, when we draw one positive and one negative example at random, the decision function assigns a higher value to the positive than to the negative example.

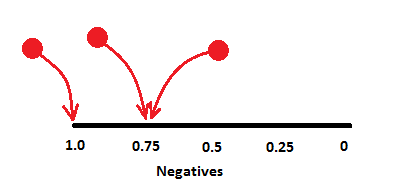
There is, however, yet another, to my mind even more intuitive, interpretation. Define the rank of a positive example as the proportion of negative examples "to the right of it" in the sorted prediction vector. For example, if the sorted prediction vector is (1, 0, 0, 0, 0), then the rank of the sole positive item there is 1.0 (all negative examples are to the right). If the sorted prediction vector is (0, 0, 1, 0, 0), the rank is 0.5 (half of negative examples is to the right), and if the vector is (0, 0, 0, 0, 1), the rank is 0. In our chocolate bar example, the ranks of the positive examples are the following:

The "rank" thus denotes where would a classifier position a given positive item within the set of negative examples, whether closer to the "left" (rank 1) or closer to the "right" (rank 0).

Now the average rank of all the positive examples seems like a reasonable metric of classifier performance, doesn't it? In fact, is exactly the ROC AUC! Now the value of 0.80 ROC score can be interpreted intuitively as follows: "the average positive example has about 20% of negative examples scored higher than it". This, so far, seems to me personally to be the "simplest" interpretation of the ROC AUC. So write it down:

ROC AUC is the average positive rank.

I've recently stumbled upon a simple observation, which does not seem to be common knowledge and yet looks quite enlightening. Namely: polynomials provide an excellent way of modeling data in an order-agnostic manner.

The situations when you need to represent data in an order-agnostic way are actually fairly common.  Suppose that you are given a traditional sample and are faced with a task of devising a generic function of the sample, which could only depend on the values in the sample, but not on the ordering of these values. Alternatively, you might need to prove that a given statistic is constant with respect to all permutations of the sample. Finally, you might simply wish to have a convenient mapping for your feature vectors that would lose the ordering information, but nothing else.

The most common way of addressing this problem is sorting the sample and working with the order statistics  instead of the original values. This is not always convenient. Firstly, the mapping of the original sample to the corresponding vector of order statistics (i.e. the sorting operation) is quite complicated to express mathematically. Secondly, the condition that the vector of order statistics is always sorted is not very pleasant to work with. A much better idea is to represent your data as a polynomial of the form

This will immediately provide you with a marvellous tool: two polynomials and are equal if and only if their roots are equal, which means, in our case, that the samples and are equal up to a reordering.

Now in order to actually represent the polynomial we can either directly compute its coefficients

or calculate its values at any different points (e.g. at ) - in any case we end up with the same amount of data as we had originally (i.e. values), but the new representation is order-agnostic and has, arguably, much nicer properties than the order statistics vector.

It is not without its own problems, of course. Firstly, it requires at least time to compute. Secondly, not every polynomial will have real-valued roots. And thirdly, the interpretation of the new "feature vector" is not necessarily intuitive or meaningful. Yet nonetheless, it's a trick to consider.

There seems to be a wide split of opinions between theoreticians and practitioners. Namely, some theoreticians define pseudorandomness in terms of complexity theory. As a result, the corresponding constructions are inherently slow and thus rejected by practitioners. This short blog post tries to address some common misconceptions.

A random number generator by xkcd

Formally, a pseudorandom generator is a deterministic function which takes a (relatively short) seed and converts it into an element of . In most cases, we as computer scientists are interested in functions . However, there are other reasonable domains, too. For instance, when performing Monte-Carlo integration in the region , we would be interested in the functions of type .

It is important to note that any function of type is a pseudorandom generator. However, not all of those functions are equally good for all purposes. There are two main properties that are used to discriminate between various pseudorandom functions. First, we can talk about the efficiency of a pseudorandom generator, i.e., how fast can we compute . Second, we can talk about the statistical properties of the output .

Before going into the details, let us establish why anyone should use pseudorandom generators at all. There is an interesting controversy in the computer science, as well in statistics. Many algorithms assume that it is possible to use uniformly distributed numbers. For example, Monte-Carlo integration is based on the law of large numbers:

whenever are taken independently and uniformly from the range . Similarly, one can provide theoretical bounds for the randomized version of quicksort, provided that we can draw elements uniformly from a set . However, computers are mostly made of deterministic parts and it turns out to be really difficult to automatically collect uniformly distributed bits. A design of a device that would solve this problem is far from trivial.

The first official solution to this problem was posed in 1927 when a student of Karl Pearson published a table of random numbers. Later such tables were built by the RAND Corporation. That is, the function  was explicitly specified through a big table. Of course, such a table is useful only if it can be used as a "reliable" source of random numbers. In particular, the value of

should be as close to as possible. Since there are infinite number of functions, we cannot actually check this condition. Instead, statisticians performed a series of tests on the table to verify that the sequence looks as close to random as possible.  If we extend this concept properly, we get the modern quantification of pseudorandomness.

Formally, a function is a -secure pseudorandom generator if for any -time algorithm :

where the probabilities are taken over the uniform choices of and . In more intuitive terms, if you replace the randomness with  and your algorithm runs in time , then the switch generates no easily observable discrepancies.

As an illustrative example, consider a probabilistic combinatorial search algorithm  that runs in time and outputs a solution that can be verified in time . In this case, the use of a -secure pseudorandom generator within instead of pure randomness would decrease the probability of finding a solution by at most . Indeed, otherwise we could construct a -time algorithm that outputs 1, if finds the solution and 0 otherwise, and use it to discern the pseudorandom generator from true randomness with success at least . This would contradict the fact that we have a true -secure pseudorandom generator.  Similar argument can be proven also for the Monte-Carlo integration algorithm. Note that parameters and  can be arbitrary real numbers. For the combinatorial search algorithm that takes 3 weeks CPU time, you might use a -secure pseudorandom generator.

There are essentially two reasonable complaints about the pseudorandom generators. First, since obtaining random bits is hard, we have not solved the problem completely, as we must still get the seed from somewhere. This is indeed a valid problem. For instance, the standard rand() function in C is known to fail the NIST statistical test and thus you might actually observe inconsistencies when using rand() directly or generating a seed for a more complex function with rand(). The latter does not mean that rand() is not a pseudorandom generator, rather that its quality might be low for certain applications. As a complete solution, you would like to get a function . For some tasks, such as Monte-Carlo integration of certain functions the corresponding solution is known (see multidimensional integration and sparse grids).

However, we still do not know how to do it in general, i.e., how to convert randomized algorithms into deterministic ones without significant losses in their performance. The corresponding area of research is known as derandomization. Second, one might argue that we could prove directly that by replacing  with , the performance of the algorithm does not deteriorate much. However, this is not an easy task and it is usually not a valid option for usual mortals.

To summarize, whenever you use a certain function to extend a random seed in your implementation you actually have to believe that it does not affect performance, i.e., is a pseudorandom generator with appropriate  parameter values. Whether you should use , rand() in C, or something more elaborate, depends on the application.