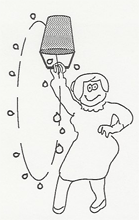
Inspired by Swen
-
Tags: Comic, Fun, Geekness, Statistics
-
Every Spring thousands of aspiring undergraduates spend numerous diligent hours working on their final theses, suffering the stress of the deadlines and the tempting pressure of the nice weather. Once they are done writing, they defend their work in public. In the end, they are graded by their supervisors, opponents and an academic committee. The grading rules might vary among universities and faculties, but their essence can be abstracted as follows: the supervisor provides a mark representing his opinion, the opponent provides a mark representing his opinion, and the final grade is obtained by taking the average of the two.
However, this process is not necessarily as simple as it looks like from the first glance. Although both the supervisor and the opponent are supposed to announce "the mark, representing their opinion", they are knowledgeable of the final grading scheme and might in fact, perhaps unconsciously, play a somewhat different game. Indeed, if the supervisor believes the student's work is worth a 4, he is in fact interested that final grade would be 4, no more and no less. The same holds for the opponent. Now let us assume that the difference between the proposed mark and the final mark measures the "penalty" for both the supervisor and the opponent. We could then regard the whole grading process as the following game.
- The supervisor has his opinion about the proper mark
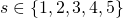 . Similarly, the opponent has his opinion about the proper mark
. Similarly, the opponent has his opinion about the proper mark 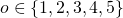 .
. - The supervisor announces the mark
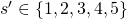 , the opponent announces the mark
, the opponent announces the mark 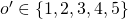 . The final grade
. The final grade 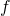 is computed as the average
is computed as the average 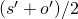 .
. - The supervisor receives penalty
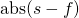 and the opponent receives penalty
and the opponent receives penalty 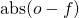 .
. - Naturally, both parties are interested in minimizing the penalty.
Now, assuming that both the supervisor and the opponent are indeed playing the above game, how would they act? Of course, this depends on their "true" opinions s and o, and whether they are knowledgeable of each other's opinion or not. For simplicity, let us first consider the case where s = o = 4 and both parties know it. In this case, we can represent the game in the traditional matrix form:
s' o' 1 2 3 4 5 1 3 2.5 2 1.5 1 2 2.5 2 1.5 1 0.5 3 2 1.5 1 0.5 0 4 1.5 1 0.5 0 0.5 5 1 0.5 0 0.5 1 Penalty for both supervisor and opponent for various choices of s' and o'There are three optimal solutions here — (s'=3,o'=5), (s'=4,o'=4) and (s'=3,o'=5), with the logical (4,4) choice being the "safest" for both parties in terms of the maximal possible penalty in case the opposing party presumed a different optimal solution.
Now what if s and o are different. For example, s = 4 and o = 3. In this case, the payoffs of the supervisor and the opponent are not equal any more:
s' o' 1 2 3 4 5 1 3 | 2 2.5 | 1.5 2 | 1 1.5 | 0.5 1 | 0 2 2.5 | 1.5 2 | 1 1.5 | 0.5 1 | 0 0.5 | 0.5 3 2 | 1 1.5 | 0.5 1 | 0 0.5 | 0.5 0 | 1 4 1.5 | 0.5 1 | 0 0.5 | 0.5 0 | 1 0.5 | 1.5 5 1 | 0 0.5 | 0.5 0 | 1 0.5 | 1.5 1 | 2 Penalties for supervisor and opponent (separated by | ) for various choices of s' and o'There are two Nash equilibrium solutions to this game and it is funny to see that none of them is the seemingly logical (4,3) choice. Instead, they are (5,1) and (1,5), the former being somewhat preferable to the supervisor. That means, the equilibrium strategy dictates the supervisor to suggest the mark 5 (which exceeds his opinion), to which the opponent should respond with a drastically low evaluation of 1. Looks like a rather typical thesis defence scenario, doesn't it? 🙂
Finally, when the true s and o are not known by the opponent and the supervisor correspondingly, the analysis becomes more complicated, because the players now have to assume something about the opponent. But the conclusion stays the same — whenever the supervisor has the slightest doubt that the opponent might be willing to suggest a lower mark, he will have to pick the overestimation strategy. And the opponent will then naturally tend to drastically underestimate.
By this weird post I actually wanted to express sincere congratulations to those who have succesfully defended this year, in particular my diligent bachelor students Anastasia, Karl and Riivo.
Tags: Fun, Game theory
- The supervisor has his opinion about the proper mark
-
Tags: Comic, Fun, Humor, Mathematics, Philosophy
-
The yachts parked in the port of Palma de Mallorca might very well outnumber the presumably plentiful palm trees in this city. The photo below depicts just a small piece of the 3 kilometer-long marina, stretched along the Paseo Maritimo coastline.
For the fun of it, let's try counting the yachts on this photo. Even though it is perhaps one of the most useless exercises one might come up with, I find it amusing and not without a relation to a variety of more serious applications. Naturally, no sane computer scientist would attempt to do the counting manually when he can let a computer do this job for him. Therefore, we'll use a chance here to exploit the fantastic Scilab Image Processing toolbox.
Preprocessing
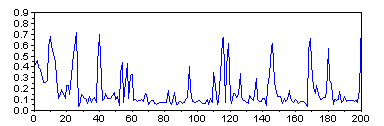
If we only want to know the number of masts, we don't need the whole image, a single line of the image that crosses all of the masts would suffice. Some pixels of this line will correspond to the sky — a brief examination shows that the RGB colour of these pixels is approximately (0.78, 0.78, 0.78). The remaining pixels will be the masts and the ropes. For each pixel, we can compute how similar this pixel's colour is to the colour of the sky (the simple euclidean distance will do OK), and thus we shall end up with a single vector, the peaks in which will correspond to the masts we need to count.
// Read image img = imread("yachts.jpg"); // Get the proper line img_line = img(505,:,:); // Subtract sky colour img_line = sqrt(sum((img_line - 0.78*ones(img_line)).^2, 3));Let us now do the counting.
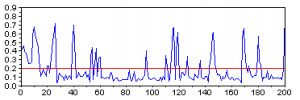
1. Geometric approach
A look on the picture above will tell you that a threshold of about 0.2 might be good for discriminating the masts from the background. Once we apply it, there are at least two easy ways to derive the number of masts.
- Firstly, we could count the number of pixels over the threshold and divide it by four, which seems like roughly the average width of a mast.
answer = sum(img_line > 0.2)/4
The result is ~135.
- Secondly, we could count the number of times the pixel value crosses the 0.2 boundary:
answer = sum(img_line(2:$) > 0.2 & img_line(1:($-1)) <= 0.2);
Here the result will be 158.
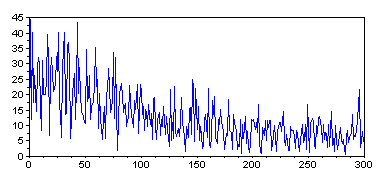
2. Spectral approach
The discrete Fourier transform of a vector is a natural way for counting repeating peaks in the signal.
ff = abs(fft(center(img_line))); plot(0:300, ff(1:301));
The interpretation of the resulting figure should, in theory, be simple. If the photo only contained n uniformly distributed masts, the spectrum would have one clear peak at n. In our case, unfortunately, things do not seem to be as easy. With some wishful thinking one might see major peaks around 50, 150 and 300. Now taking the previous results into consideration let us presume that 150 is the correct peak. Then 50 could correspond to the 50 "larger" masts on the image, and 300, perhaps, to the ropes.
3. Statistical approach
The original image is 1600 pixels wide. If the photo contained n masts, distributed uniformly along its width, a randomly chosen 32-pixel region would contain about n/50 masts on average. Therefore, let us select some of these random regions and count the number of masts in them manually. After multiplying the resulting numbers by 50 we should obtain estimates of the total number of masts.
xbasc(); rand("seed", 1); for i=1:9 m = floor(rand()*(1600-32))+1; subplot(3,3,i); imshow(img([474:566], [m:(m+32)],:)) endHere are the estimates I got here: 200, 50, 50, 150, 150, 100, 100, 100, 100. The average comes at 111 with a standard deviation of about 50.
Summary
There are serious discrepances among the results produced by various approaches. However, if you attempt to count the masts manually, you will quickly discover that there is indeed an inherent degree of uncertainty in the number of visible masts, with the true number lying somewhere between 100 and 150. Consequently, the considered approaches to mast counting were not too far off, after all.
Tags: Fun, Image processing, Scilab, Travel
- Firstly, we could count the number of pixels over the threshold and divide it by four, which seems like roughly the average width of a mast.
-
Everyone, who flies reasonably often has a chance to observe a remarkable effect: no matter how steep the roll angle of an airliner is during a turn, the tea in your cup will always stay parallel to the floor, and not to the ground. In the course of one recent unexpectedly long discussion on this topic, it turned out there is no much easily googleable material out there to refer to. I thought I'd create some, hence a somewhat longer post on an otherwise simple matter of minor relevance to my main affairs.
So, firstly, why doesn't tea orient itself parallel to the ground? To understand that, consider a pair of insightful examples. They should rid you of the incorrect intuitive assumption that it is gravity, which plays a defining role in the orientation of your tea.
Example 1: Water in the bucket
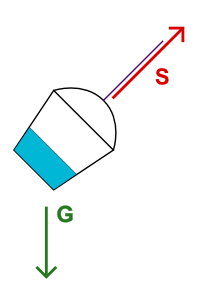
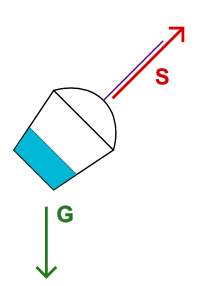
Consider the experiment described in the previous post about a water bucket on a string. No matter what you do with the bucket, as long as the string is at strain, the water will stay parallel to bottom of the bucket, and not to the ground. The explanation for that is the following. Water is affected by gravity G. The bucket is affected by gravity G and the strain of the string S. Therefore, from the frame of reference of the bucket, water experiences force G-(G+S) = -S, which pulls it towards the bottom of the bucket.
Example 2: Paragliders
You have probably seen paragliders in the air. If not, just search for "extreme paragliding" on youtube. Note that whatever the angle of the wing, the person is always hanging perpendicularly to it. Now if you'd hand him a bottle with water, the water would, naturally, also orient itself in parallel to the wing. The reason of that behaviour is the same as in the water bucket experiment, with the lift of the wing playing the same role as the strain of the string.
The main idea of both examples is that as long as the container and the object inside it are equally affected by gravity, it is not gravity that orients the object with respect to the container. More precisely, for the water to incline to the side, there must be some force acting on the container from that side.
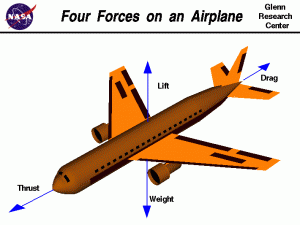
The Airplane: A Simple Model
Let us now consider an idealized airplane. According to a popular model, an airplane in flight is affected by four forces: the thrust of the engines T, the drag due to air resistance D, the lift of the wings L and the gravitational weight of the airplane G. The glass of tea inside the airplane is, of course, only affected by gravity G. By applying the same logic as before, we can easily compute, that in the frame of reference of the airplane, the tea is experiencing acceleration F = G-(T+D+L+G) = -(T+D+L).However, once the airplane has attained constant speed (which is true for most of the duration of the flight), its thrust is completely cancelled by the air resistance, i.e. T+D = 0, in which case F = -L. It now remains to note that the lift force of the wings is always approximately perpendicular to the wings and thus to the floor of the airliner. The tea in your cup must therefore indeed be parallel to the floor.
The Airplane: A More Realistic Model
The model considered in the previous section is somewhat too simplistic. According to it there are no forces acting on the sides of the airplane whatsoever, and it should therefore be absolutely impossible to incline the tea in the cup to the side, which is, of course, not true for a real airplane. So, assuming a pilot would want to incline the tea and spill it, what would be his options?- Thrust. As noted above, tea must only be parallel to the floor when thrust is perfectly cancelled by drag and the plane is moving with constant speed. A rapid increase or decrease in thrust could therefore incline the tea towards or against the direction of flight. But of course, there is usually no need for such a maneuver during a passenger flight except for takeoff and landing.
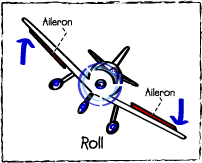
- Rotation. The model above does not consider the fact, that the pilot may use the ailerons and rudder to turn the airplane, rotating it around its axes. And of course, when the resulting rotation is abrupt enough, the tea could incline somewhat. However, during passenger flights the turns are always performed very smoothly, with rotation speeds around 1 degree per second. In fact it is risky, if not impossible to perform any hasty rotationary maneuvers on an airliner travelling at about 800km/h.
-
Slip. The simple model above considered the case when the air is flowing directly along the main axis of the airplane, which need not necessarily always be the case. The condition may be violated either due to a strong sidewind, or during a peculiar kind of a turn, where the airplane "slips" or "skids" on the side. In both cases, the airflow is exerting pressure on the side of the airplane's hull, which generates the so-called body lift. It is usually incomparably smaller than the lift of the wings, but nonetheless, it can incline the water to the side.
It is interesting to understand why you should almost never experience slip in an airliner. There are two reasons for that. Firstly, most airplanes have a degree of weathercock stability. Like a weathercock, an airplane with a vertical tail stabilizer tends to automatically orient itself into the direction of airflow and thus avoid slip. This effect is especially strong at the speed of a commercial airliner.
Secondly, if the weathercock effect is not enough to prevent slip, the pilot himself will always ensure that the slip is never too large by watching the slip-indicator (aka inclinometer) and coordinating the turn.
Why that? Because the airplane is not constructed, aerodynamically, to fly sideways. When the plane is moving sideways, the body of the plane blocks airflow over the trailing wing. So the wing loses lift and begins to drop. This naturally will put the airplane into a bank in the direction of the turn, but it does so at great cost in drag. When the slip is too large the lifting properties of the wings change so drastically that this might put the airplane at the risk of a crash.
Summary
Q: Why is the tea in an airliner parallel to the floor even when the airplane is turning?
A: It follows from the following three conditions, that must all be satisfied for a safe flight:- The forces of thrust and drag cancel each other and the airplane moves at a constant speed.
- The turns are performed smoothly.
- There is no slip: the air flows directly along the main axis of the airplane.
-
Most of us probably remember this experiment from high school physics lessons: you take a bucket on a string filled with water, spin it around your head and the water does not spill. "But how?" - you would ask in amazement. And the teacher would explain then:
"You see, the bucket is spinning, and this creates the so-called centrifugal force acting on the water, which cancels out gravity and thus keeps the water in the bucket". And you will have a hard time finding any other explanation. At least I failed no matter how hard I googled it.Unfortunately, this explanation looses an essential point of the experiment and I have seen people irreparaply braindamaged by the blind belief that it is only due to rotation and the resulting virtual centrifugal force that the water does not spill.
However, it is not quite the case. Let us imagine that the bucket has accidentally stopped right over your head and as a result, all centrifugal force has been immediately lost. Would the water spill? It will certainly fall down on your head, but it will do so together with the bucket. Thus, technically, the water will stay inside the bucket.
In fact, the proper way to enjoy the true magic of the experiment is not to swing the bucket in full circles, but rather let it swing back and forth as a pendulum (if you have a string and a beverage bottle nearby, you can do an experiment right now). One will then observe that even at the highest points of the swing, where the bottom of the bucket is at its steepest angle and the centrifugal force is nonexistant, the water stays strictly parallel to the bottom of the bucket, as if no gravity would act upon it. Why doesn't it spill? Clearly, the argument of centrifugal force cancelling gravity is inappropriate.
The proper explanation is actually quite simple and much more generic. We have two objects here: the bucket and the water in it. There is one (real) force acting on the water: gravity G. There are two (real) forces acting on the bucket: gravity G and the strain S of the string pulling the bucket perpendicularly to its bottom. (Note that the centrifugal force is not "real" and I do not consider it here, but if you wish, you may. Just remember then that it acts both on the water and the bucket.)
Now the question of interest is, how does water behave with respect to the bucket? That is, what force "pulls" the water towards the bucket and vice-versa. This can be easily computed by subtracting all forces acting on the bucket from all forces acting on the water. And the result is, of course, G - (S+G) = -S, i.e. a force, pulling the water directly towards the bottom of the bucket.A magical consequence of this argument is that gravity does not matter inside the bucket, as long as it can act on the bucket freely in the same way as on anything inside it. Nothing special about rotation here, really. It takes a while to realize.
Tags: Conspiracy, Experiment, Fun, Physics
-
Two hardened criminals are taken to interrogation in separate cells.
They are offered the usual deal:
If neither confesses, both get one year probation.
If both confess, both do 5 years in jail.
If one confesses, he goes free but the other does 10 years hard time.Here's what actually goes through their minds:
"Okay, if neither of us confesses, we have to go back to the real world. But its so hard there!
But if I confess, he will kill me when he gets out.. so thats bad...
If both of us confess, then we can just get back to jail and continue our lives!"Note that it shares some similarities with the original...
Tags: Fun, Game theory
-
Consider the following excerpt from a recent article in the British Medical Journal:
Mike has only two children, and they are called Pat and Alex, which could equally be boys’ or girls’ names. In fact, Pat is a girl. What is the probability that Alex is a boy?
a 50%
b Slightly less than 50%
c Slightly more than 50%
d Between 60% and 70%
e Between 40% and 30%d—Although this could be about the relative popularity of ambiguous names for boys and girls or about subtle imbalances in the sex ratio, it is not meant to be. The clue to the correct answer is in thinking about what we do not know about the family and what we do know already, and applying this to the expected probabilities of girls and boys.
We do not know if Pat was born first or second. We do know that there are only two children and that Pat is a girl. I am assuming that in the population, 50% of children are girls.
The birth order and relative frequency of two child families are: boy, boy (25%), girl, girl (25%), boy, girl (25%) girl, boy (25%). We know Mike’s family does not have two boys, since Pat is a girl, so we are only left with three choices for families with at least one girl. Two of these pairs have a boy and one does not. Hence the probability that Alex is a boy is two thirds or 66.7%.
If we had been told that Pat was born first then the probability that Alex is a boy drops to 50%.
The well-known "Boy or Girl" paradox that is referenced in the fragment above is probably as old as the probability theory itself. And it is therefore quite amusing to see an incorrect explanation for it presented in a serious journal article. You are welcome to figure out the mistake yourself.
For completeness sake, here is my favourite way of presenting this puzzle:
In the following, let Mike be a randomly chosen father of two kids.
- Mike has two kids, one of them is a boy. What is the probability that the other one is a girl?
- Mike has two kids, the elder one is a boy. What is the probability that the other one is a girl?
- Mike has two kids. One of them is a boy named John. What is the probability that the other one is a girl?
- I came to visit Mike. One of his two kids, a boy, opened the door to me. What is the probability that Mike's other child is a girl?
- I have a brother. What is the probability that I am a girl?
- I have a brother named John. What is the probability that I am a girl?
You can assume that boys and girls are equiprobable, the births of two kids are independent events, a randomly chosen boy will be named John with probability p, and that a family may have two kids with the same name.
If you haven't tried solving these yet, give it a try. I'm pretty sure you won't do all 6 questions correctly on the first shot.
Tags: Fun, Paradox, Probability theory, Puzzle
-
The amusing fact that Minesweeper was proven to be NP-complete is quite well known in certain circles. However, it seems that no one has yet cared to publicly demonstrate the (probably obvious, but not a single bit less amusing) fact, that constructing LEGO toys is also an NP-complete task. Here I fix this disturbing flaw and present a reduction of SAT to LEGO by a simple example.
Suppose you are given the following set of LEGO blocks
and you wish to construct the following structure from them (using only this picture as a reference):
It turns out that devising such a configuration is equivalent to finding a satisfying assignment for the boolean formula
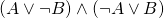 , and it is possible to devise an analogous configuration for any other logical formula in CNF. Thus, building LEGO must be at least as hard as satisfying boolean formulas, that is, NP-hard.
, and it is possible to devise an analogous configuration for any other logical formula in CNF. Thus, building LEGO must be at least as hard as satisfying boolean formulas, that is, NP-hard.Indeed, let the red brick correspond to the variable
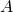 , the blue brick let be
, the blue brick let be 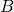 , the pink brick
, the pink brick 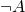 and the light blue brick
and the light blue brick 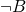 .
.
Consider the part I of the target configuration (the one in the upper left). It contains one red brick and one light blue brick, but because of the black block in front of them we don't know whether the red and the light blue bricks are of height 1 or 2. There are three possible options:We say that this configuration corresponds to the term
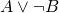 , where having a higher brick for a given variable corresponds to setting the value of that variable to True. Clearly, for the configuration to be possible either the red brick (
, where having a higher brick for a given variable corresponds to setting the value of that variable to True. Clearly, for the configuration to be possible either the red brick (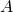 ) or the light blue brick (
) or the light blue brick (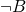 ) must be high, and therefore a proper choice of bricks here corresponds to a choice of values in the expression
) must be high, and therefore a proper choice of bricks here corresponds to a choice of values in the expression 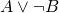 . Analogously, part II corresponds to the term
. Analogously, part II corresponds to the term 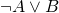 and the fact that both parts are possible translates to the full equation
and the fact that both parts are possible translates to the full equation 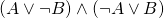 .
.Now what about parts III and IV? These guarantee that if we choose the high red brick when constructing parts I and II, we shall necessarily have to use the shorter pink brick there, and similarly for the blue and light blue bricks. Indeed, due to the choice of white bricks there are two ways of constructing part III:
In the first case we use up the high red brick and the short pink brick for constructing part III, and therefore end up with the short red brick and high pink brick for building parts I and II. This corresponds to picking the value False for
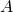 . Similarly, the second way of constructing part III would enforce the value True for the variable
. Similarly, the second way of constructing part III would enforce the value True for the variable 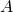 .
.A short reflection should convince you now, that the same scheme can be used to represent any other CNF boolean expression. As it is well known that finding a satisfying assignment for a boolean formula is NP-complete, it follows that LEGO is NP-complete too.
Q.E.D.
Tags: Complexity theory, Fun, LEGO
-
This week I had a chance to participate in a project meeting related to soft computing. A part of the meeting was a brainstorm-like session, dedicated to the generation of relevant topics for future research in the field. I was listening very carefully, writing everything down, and trying to generalize somewhat. By the end of the meeting my generalization attempts succeeded and now I can easily generate relevant topics in arbitrary numbers without any external help. In an act of openness, unprecedented elsewhere in scientific circles, I'm sharing this secret technology with you here.
For the curious: here is the source code.
Tags: Fun, Language, Project, Soft computing
Calendar
| M | T | W | T | F | S | S |
|---|---|---|---|---|---|---|
| « Jan | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | |||
Recent Comments
Archives
- January 2024 (1)
- October 2019 (1)
- February 2019 (1)
- November 2018 (1)
- June 2018 (1)
- April 2018 (1)
- March 2018 (1)
- December 2017 (1)
- July 2017 (2)
- May 2017 (1)
- March 2017 (4)
- November 2016 (3)
- July 2016 (2)
- May 2016 (1)
- January 2016 (2)
- September 2015 (2)
- July 2015 (1)
- June 2015 (1)
- May 2015 (1)
- April 2015 (3)
- March 2015 (3)
- January 2015 (2)
- March 2014 (2)
- January 2014 (1)
- April 2013 (1)
- February 2013 (2)
- January 2013 (1)
- November 2012 (1)
- October 2012 (2)
- September 2012 (2)
- June 2012 (1)
- May 2012 (1)
- January 2012 (3)
- December 2011 (2)
- October 2011 (3)
- May 2011 (1)
- March 2011 (1)
- June 2010 (1)
- February 2010 (2)
- November 2009 (1)
- October 2009 (3)
- August 2009 (2)
- June 2009 (1)
- March 2009 (3)
- February 2009 (3)
- January 2009 (5)
- December 2008 (4)
- November 2008 (3)
- October 2008 (7)
- September 2008 (8)