Four Years Remaining

Consider the following question:

Which of the following two statements is logically true?

1. All planets of the Solar System orbit the Sun. The Earth orbits the Sun. Consequently, the Earth is a planet of the Solar System.
2. God is the creator of all things which exist. The Earth exists. Consequently, God created the Earth.

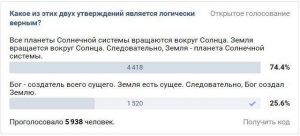I've seen this question or variations of it pop up as "provocative" posts in social networks several times. At times they might invite lengthy discussions, where the participants would split into camps - some claim that the first statement is true, because Earth is indeed a planet of the Solar System and God did not create the Earth. Others would laugh at the stupidity of their opponents and argue that, obviously, only the second statement is correct, because it makes a valid logical implication, while the first one does not.

Not once, however, have I ever seen a proper formal explanation of what is happening here. And although it is fairly trivial (once you know it), I guess it is worth writing up. The root of the problem here is the difference between implication and provability - something I myself remember struggling a bit to understand when I first had to encounter these notions in a course on mathematical logic years ago.

Indeed, any textbook on propositional logic will tell you in one of the first chapters that you may write

to express the statement " implies ". A chapter or so later you will learn that there is also a possibility to write

to express a confusingly similar statement, that " is provable from ". To confirm your confusion, another chapter down the road you should discover, that is the same as , which, in turn, is logically equivalent to . Therefore, indeed, whenever is true, is true, and vice-versa. Is there a difference between and then, and why do we need the two different symbols at all? The "provocative" question above provides an opportunity to illustrate this.

The spoken language is rather informal, and there can be several ways of formally interpreting the same statement. Both statements in the puzzle are given in the form ", , consequently ". Here are at least four different ways to put them formally, which make the two statements true or false in different ways.

The Pure Logic Interpretation

Anyone who has enough experience solving logic puzzles would know that both statements should be interpreted as abstract claims about provability (i.e. deducibility):

As mentioned above, this is equivalent to

or

In this interpretation the first statement is wrong and the second is a correct implication.

The Pragmatic Interpretation

People who have less experience with math puzzles would often assume that they should not exclude their common sense knowledge from the task. The corresponding formal statement of the problem then becomes the following:

In this case both statements become true. The first one is true simply because the consequent is true on its own, given common knowledge (the Earth is indeed a planet) - the antecedents and provability do not play any role at all. The second is true because it is a valid reasoning, independently of the common knowledge.

This type of interpretation is used in rhetorical phrases like "If this is true, I am a Dutchman".

The Overly Strict Interpretation

Some people may prefer to believe that a logical statement should only be deemed correct if every single part of it is true and logically valid. The two claims must then be interpreted as follows:

Here the issue of provability is combined with the question about the truthfulness of the facts used. Both statements are false - the first fails on logic, and the second on facts (assuming that God creating the Earth is not part of common knowledge).

The Oversimplified Interpretation

Finally, people very unfamiliar with strict logic would sometimes tend to ignore the words "consequently", "therefore" or "then", interpreting them as a kind of an extended synonym for "and". In their minds the two statements could be regarded as follows:

From this perspective, the first statement becomes true and the second (again, assuming the aspects of creation are not commonly known) is false.

Although the author of the original question most probably did really assume the "pure logic" interpretation, as is customary for such puzzles, note how much leeway there can be when converting a seemingly simple phrase in English to a formal statement. In particular, observe that questions about provability, where you deliberately have to abstain from relying on common knowledge, may be different from questions about facts and implications, where common sense may (or must) be assumed and you can sometimes skip the whole "reasoning" part if you know the consequent is true anyway.

Here is an quiz question to check whether you understood what I meant to explain.

"The sky is blue, and therefore the Earth is round." True or false?

Ever since the "Prior Confusion" post I was planning to formulate one of its paragraphs as the following abstract puzzle, but somehow it took me 8 years to write it up.

According to fictional statistical studies, the following is known about a fictional chronic disease "statistite":

1. About 30% of people in the world have statistite.
2. About 35% of men in the world have it.
3. In Estonia, 20% of people have statistite.
4. Out of people younger than 20 years, just 5% have the disease.
5. A recent study of a random sample of visitors to the Central Hospital demonstrated that 40% of them suffer from statistite.

Mart, a 19-year Estonian male medical student is standing in the foyer of the Central Hospital, reading these facts from an information sheet and wondering: what are his current chances of having statistite? How should he model himself: should he consider himself as primarily "an average man", "a typical Estonian", "just a young person", or "an average visitor of the hospital"? Could he combine the different aspects of his personality to make better use of the available information? How? In general, what would be the best possible probability estimate, given the data?

Most results that are published in mathematics and natural sciences are highly technical and obscure to anyone outside the particular area of research. Consequently, most scientific publications and discoveries do not get any media attention at all. This is a problem both for the public (which would benefit from knowing a bit more about our world), the science in general (which would benefit from wider dissemination) and the scientists themselves (which would certainly appreciate if their work reached more than a couple of other people). The issue is usually addressed by the researchers trying to popularize their findings — provide simple interpretations, which could be grasped by the layman without the need to understand the foundations. Unfortunately, if the researcher was lucky to grab enough media attention, chances are high the process of "popularization" will get completely out of hands, and the message received by the public will have nothing to do with the original finding.

There are some theorems in pure mathematics, which happened to suffer especially seriously from this phenomenon. My two most favourite examples are the Heizenberg's uncertainty principle and Gödel's incompleteness theorems. Every once in a while I stumble on pieces, written by people who have zero knowledge of basic physics (not even mentioning quantum mechanics or Fourier theory), but claim to have clearly understood the meaning and the deep implications of the uncertainty principle upon our daily lives. Even more popular are Gödel's theorems. "Science proves that some things in this world can never be understood or predicted by us, mere humans!!!" is a typical take on Gödel by the press. Oh, and it is loved by religion enthusiasts!

This post is my desperate attempt to bring some sanity back into this world by providing a (yet another, but maybe slightly different) popular explanation for Gödel's ideas.

Gödel's theorems explained (with enough context)

Kurt Gödel

In our daily lives we primarily use symbols to communicate and describe the world. Those may be formulas in mathematics or simply sentences in the English language. Symbol-based systems can be used in different ways. From the perspective of arts and humanities, one is welcome to construct arbitrary sequences of words and sentences, as long as the result is "beautiful", "inspiring" or "seems smart and convincing". From a more technically-minded point of view, however, one is only welcome to operate with "true and logical" statements. However, it is not at all obvious which statements should be universally considered "true and logical". There are two ways the problem can be resolved.

Firstly, we can determine the truth by consulting "reality". For example, the phrase "All people are mortal, hence Socrates is mortal" is true because, indeed (avoiding a lecture-worth of formalities or so), in all possible universes where there are people and they are mortal, Socrates will always also be mortal.

Secondly, we can simply postulate a set of statements, which we shall universally regard as "the true ones". To distinguish those postulated truths from the "actual truths", mentioned in the paragraph above, let us call them "logically correct statements". That is, we can hypothetically write down an (infinite) list of all the "logically correct" sentences in some hypothetical "Book of All Logically Correct Statements". From that time on, every claim not in the book will be deemed "illogical" and hence "false" (the question of whether it is false in reality would, of course, depend on the goodness and relevance of the book we created).

This is really convenient, because now in order to check the correctness of the claim about Socrates we do not have to actually visit all the possible universes. It suffices to look it up in our book! If the book is any good, it will provide good answers, so the concept of "logical correctness" may be close or even equivalent to "actual truth". And in principle, there must exist "The Actual Book of Truth", which would list precisely the "actually true" statements.

Unfortunately, infinite books are somewhat inconvenient to print and carry around. Luckily, we can try to represent an infinite book in a finite way using algorithms. We have all seen how a short algorithm is capable of producing an infinite amount of nonsense, haven't we? Thus, instead of looking for an (infinitely-sized) "book of truth", we should look for a (finitely-sized) "algorithm of truth", which will be either capable of generating the whole book, or checking for any given statement, whether it belongs to the book.

Frege's propositional calculus

For clarity and historical reasons,  the algorithms for describing "books of truths" are usually developed and written down using a particular "programming language", which consists of "axioms" and "inference rules". Here is one of the simplest examples of how a "program" might look like.

This is where a natural question arises: even if we assume that we have access to "the actual book of truth", will it really be possible to compress it down to a finite algorithm? Isn't it too much to ask? It turns out it is. There is really no way to create a compact representation for any but the most trivial "books of truths".

Besides the "asking too much" intuition, there are at least two other simple reasons why this is impossible. Firstly, most of the readers here know that there exist problems, that are in principle uncomputable. Those are usually about statements, the correctness of which cannot be checked in finite time by a finite algorithm, with the most famous example being the halting problem, as well as everything related to uncomputable numbers.

Naturally, if we can't even use a finite algorithm to list "all truly halting programs", our hopes for getting a finite description for any more complicated "book of truths" is gone. But there is another funny reason. Once we have decided to define the book with all true statements and devise an algorithm for generating it, we must not forget to include into the book some statements about the book and the algorithm themselves. In particular, we must consider the following phrase: "This sentence will not be included in the book generated by our algorithm."

If our algorithm does include this sentence in the generated book, the claim turns out to be false. As a result, our precious book would have false statements in it: it would be inconsistent. On the other hand, if our algorithm produces a book which does not include the above sentence, the sentence turns out to be true and the book is incomplete. It is just the liar's paradox.

And so it is — we have to put up with the situation, where it is impossible to produce a finite representation for all true statements without stumbling into logical paradoxes. Or, alternatively, that there are mathematical statements, which cannot be checked or proven within a finite time.

This describes what is known as "Gödel's first incompleteness theorem" (namely, the claim that in most cases our algorithm is only capable of producing either an incomplete or an inconsistent "book"). A curious corollary may be derived from it, which is known as the "Gödel's second incompleteness theorem". The theorem says that if our "book-generating algorithm" happens to include into it exactly the phrase "This book is consistent", it must necessarily be a false claim, and the algorithm must actually be inconsistent. This is often interpreted that no "honest" theory is capable of claiming it's own correctness (there are caveats, though).

Gödel's theorems have several interesting implications for the foundations of mathematics. None the less, those are still theorems about the fundamental impossibility of using a finite algorithm for generating a book of logically correct statements without stumbling into logical paradoxes and infinite loops. Nothing more and nothing less. They have nothing to do with the experimental sciences: note how we had to cut away all connections to reality in the very first paragraphs of the explanation. And thus, Gödel's theorems are not related to the causes of "human inability to grasp the universe", "failure or success of startup business plans", or anything else of that kind.

I do not know who is the author, but I think this is great: