This is a (slightly modified) write-up of a part of a lecture I did for the "Welcome to Computer Science" course last semester.
Part I. Humans Discover the World
How it all started
Millions of years ago humans were basically monkeys. Our ape-like ancestors enjoyed a happy existence in the great wide world of Nature. Their life was simple, their minds were devoid of thought, and their actions were guided by simple cause-and-effect mechanisms. Although for a modern human it might seem somewhat counterintuitive or even hard to imagine, the ability to think or understand is, in fact, completely unnecessary to succesfully survive in this world. As long as a living creature knows how to properly react to the various external stimuli, it will do just fine. When an ape sees something scary — ape runs. When an ape seems something tasty — ape eats. When an ape sees another ape — ape acts according to whatever action pattern is wired into its neural circuits. Does the ape understand what is happening and make choices? Not really — it is all about rather basic cause and effect.
As time went by, evolution blessed our ape-like ancestors with some extra brain tissue. Now they could develop more complicated reaction mechanisms and, in particular, they started to remember things. Note that, in my terminology here, "remembering" is not the same as "learning". Learning is about simple adaptation. For example, an animal can learn that a particular muscle movement is necessary to get up on a tree — a couple of failed attempts will rewire its neural circuit to perform this action as necessary. One does not even need a brain to learn — the concentration of proteins in a bacteria will adjust to fit the particular environment, essentially demonstrating a learning ability. "Remembering", however, requires some analytical processing.
Remembering
It is easy to learn to flex a particular finger muscle whenever you feel like climbing up a tree, but it is a totally different matter to actually note that you happen to regularly perform this action somewhy. It is even more complicated to see that the same finger action is performed both when you climb a tree and when you pick a banana. Recognizing such analogies between actions and events is not plain "learning" any more. It is not about fine-tuning the way a particular cause-and-effect reflex is working. It is a kind of information processing. As such, it requires a certain amount of "memory" to store information about previous actions and some pattern analysis capability to be able to detect similarities, analogies and patterns in the stored observations. Those are precisely the functions that were taken over by the "extra" brain tissue.
So, the apes started "remembering", noticing analogies and making generalization. Once the concept of "grabbing" is recognized as a recurring pattern, the idea of grabbing a stone instead of a tree branch is not far away. Further development of the brain lead to better "remembering" capabilities, more and more patterns discovered in the surrounding world, which eventually lead to the birth of symbolic processing in our brains.
Symbols
What is "grabbing"? It is an abstract notion, a recurring pattern, recognized by one of our brain circuits. The fact that we have this particular circuit allows us to recognize further occurrences of "grabbing" and generalize this idea in numerous ways. Hence, "grabbing" is just a symbol, a neural entity that helps our brains to describe a particular regularity in our lives.
As time went by, prehistoric humans became aware (or, let me say "became conscious") of more and more patterns, and developed more symbols. More symbols meant better awareness of the surrounding world and its capabilities (hence, the development of tools), more elaborate communication abilities (hence, the birth of language), and, recursively, better analytic abilities (because using symbols, you can search for patterns among patterns).
Symbols are immensely useful. Symbols are our way of being aware of the world, our way of controlling this world, our way of living in this world. The best thing about them is that they are easily spread. It may have taken centuries of human analytical power to note how the Sun moves along the sky, and how a shadow can be used to track time. But once this pattern has been discovered, it can be recorded and used infinitely. We are then free to go searching for other new exciting patterns. They are right in front of us, we just need to look hard. This makes up an awesome game for the humankind to play — find patterns, get rewards by gaining more control of the world, achieve better life quality, feel good, everyone wins! Not surprisingly, humans have been actively playing this game since the beginning of time. This game is what defines humankind, this is what drives its modern existence.
Science

Galelio's experiment
"All things fall down" — here's an apparently obvious pattern, which is always here, ready to be verified. And yet it took humankind many years to discover even its most basic properties. It seems that the europeans, at least, did not care much about this essential phenomenon until the XVIIth century. Only after going through millenia self-deception, followed by centuries of extensive aggression, devastating epidemics, and wild travels, the europeans found the time to sit down and just look around. This is when Galileo found out that, oh gosh, stuff falls down. Moreover, it does so with the same velocity independently of its size. In order to illustrate this astonishing fact he had to climb on to the tower of Pisa, throw steel balls down and measure the fall time using his own heartbeat.
In fact, the late Renaissance was most probably the time when europeans finally became aware of the game of science (after all, this is also a pattern that had to be discovered). People opened their eyes and started looking around. They understood that there are patterns waiting to be discovered. You couldn't see them well, and you had to look hard. Naturally, and somewhat ironically, the sky was the place they looked towards the most.
Patterns in the Sky

Tycho Brahe
Tycho Brahe, a contemporary of Galileo, was a rich nobleman. As many other rich noblemen of his time, he was excited about the sky and spent his nights as an astronomer. He truly believed there are patterns in planetary motions, and even though he could not see them immediately, he carefully recorded daily positions of the stars and planets, resulting in a vast dataset of observations. The basic human "remembering" ability was not enough anymore — the data had to be stored on an external medium. Tycho carefully guarded his measurements, hoping to discover as much as possible himself, but he was not the one to find the pattern of planetary motion. His assistant, Johannes Kepler got a hold of the data after Tycho's death. He studied the data and came up with three simple laws which described the movements of planets around the Sun. The laws were somewhat weird (the planets are claimed to sweep equal areas along an ellipse for no apparent reason), but they fit the data well.
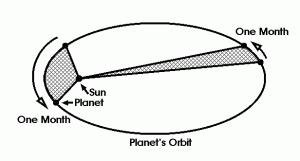
Kepler's Laws
This story perfectly mirrors basic human pattern discovery. There, a human first observes the world, then uses his brain to remember the observations, analyze them, find a simple regularity, and come up with an abstract summarizing symbol. Here the exact same procedure is performed on a larger scale: a human performs observations, a paper medium is used to store them, another human's mind is used to perform the analysis, the result is a set of summarizing laws.

Isaac Newton
Still a hundred years later, Isaac Newton looked hard at both Galileo's and Kepler's models and managed to summarize them further into a single equation: the law of gravity. It is somewhat weird (everything is claimed to be attracted to everything for no apparent reason), but it fits the data well. And the game is not over yet, three centuries later we are still looking hard to understand Gravity.
Where are we going
As we play the game, we gradually run out of the "obvious" patterns. Detecting new laws of nature and society becomes more and more complicated. Tycho Brahe had to delegate his "memory" capabilities to paper. In the 20th century, the advent of automation helped us to delegate not only "memory", but the observation process itself. Astronomers do not have to sit at their telescopes and manually write down stellar positions anymore — automated radar arrays keep a constant watch on the sky. Same is true of most other science disciplines to various extents. The last part of this puzzle which is not fully automated yet is the analysis part. Not for long...
Part II. Computers Discover the World
Manufactured life

Vacuum tube
The development of electricity was the main industrial highlight of the XIXth century. One particularly important invention of that century was an incredibly versatile electrical device called the vacuum tube. A lightbulb is a vacuum tube. A neon lamp is a vacuum tube. A CRT television set is a vacuum tube. But, all the fancy glowing stuff aside, the most important function of a vacuum tube turned out to be its ability to act as an electric current switcher. Essentially, it allowed to hardwire a very simple program:
if (wire1) then (output=wire2) else (output=wire3)
It turns out that by wiring thousands of such simple switches together, it is possible to implement arbitrary algorithms. Those algorithms can take input signals, perform nontrivial transformations of those signals, and produce appropriate outputs. But the ability to process inputs and produce nontrivial reactions is, in fact, the key factor distinguishing the living beings from lifeless matter. Hence, religious, spiritual, philosophical and biological aspects aside, the invention of electronic computing was the first step towards manufacturing life.
Of course, the first computers were not at all like our fellow living beings. They could not see or hear, nor walk or talk. They could only communicate via signals on electrical wires. They could not learn — there was no mechanisms to automaticaly rewire the switches in response to outside stimuli. Neither could they recognize and "remember" patterns in their inputs. In general, their hardwired algorithms seemed somewhat too simple and too predictable in comparison to living organisms.

Transistors
But development went on with an astonishing pace. The 1940's gave us the most important invention of the XXth century: the transistor. A transistor provides the same switching logic as a vacuum tube, but is tiny and power-efficient. Computers with millions and billions of transistors became gradually available. Memory technologies caught up: bytes grew into kilobytes, megabytes, gigabytes and terabytes (expect to see a cheap petabyte drive at your local computer store in less than 5 years). The advent of networking and the Internet, multicore and multiprocessor technologies followed closely. Nowadays the potential for creating complex, "nontrivial" lifelike behaviour is not limited so much by the hardware capabilities. The only problem left to solve is wiring the right program.
Reasoning
The desire to manufacture "intelligence" surfaced early on in the history of computing. A device that can be programmed to compute, must be programmable to "think" too. This was the driving slogan for computer science research in most of the 1950-1980s. The main idea was that "thinking", a capability defining human intellectual superiority over fellow mammals, was mainly related to logical reasoning.
"Socrates is a man. All men are mortal. => Hence, Socrates is mortal."
As soon as we teach computers to perform such logical inferences, they will become capable of "thinking". Many years of research have been put in to this area and it was not in vain. By now, computers are indeed quite successful at performing logical inference, playing games and searching for solutions of complex discrete problems. But the catch is, this "thinking" does not feel like being proper "intelligence". It is still just a dumb preprogrammed cause-and-effect thing.
The Turing Test

Alan Turing
A particular definition of "thinking" was provided by Alan Turing in his Turing test: let us define intelligence as a capability of imitating a human in a conversation, so that it would be indistinguishable from a real human. This is a hard goal to pursue. It obviously cannot be achieved by a bare logical inference engine. In order to imitate a human, computer has to know what a human knows, and that is a whole lot of knowledge. So, perhaps intelligence could be achieved by formalizing most of human knowledge within a powerful logical inference engine? This has been done, and done fairly well, but sadly, this still does not resemble real intelligence.
Reasoning by Analogy
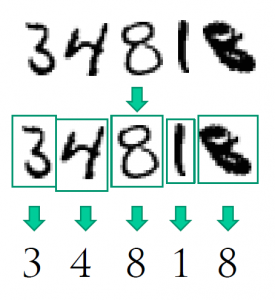
Optical character recognition
While hundreds of computer science researchers were struggling hard to create the ultimate knowledge-based logical system, real-life problems were waiting to be solved. No matter how good the computer became at solving abstract logical puzzles, he seemed helpless when faced with some of the most basic human tasks. Take, for example, character recognition. A single glimpse at a line of handwritten characters is enough for a human to recognize the letters (unless it is my handwriting, of course). But what logical inference should the computer do to perform it? Obviously, humans do not perform this task using reasoning, but rely on intuition instead. How can we "program" intuition?
The only practical way to automate character recognition turned out to be rather simple, if not to say dumb. Just store many examples of actual handwritten characters. Whenever you need to recognize a character, find the closest match in that database and voila! Of course, there are details which I sweep under the carpet, but the essence is here: recognition of characters can only be done by "training" on a dataset of actual handwritten characters. The key part of this "training" lies, in turn, in recognizing (or defining) the analogies among letters. Thus, the "large" task of recognizing characters is reduced to a somewhat "smaller" task of finding out which letters are similar, and what features make them similar. But this is pattern recognition, not unlike the rudimentary "remembering" ability of the early human ancestors.
The Meaning of Life
Please, observe and find the regularity in the following list:
- An ape observes its actions, recognizes regularities, and learns to purposefully grab things.
- Galileo observes falling bodies, recognizes regularities, and leans to predict the falling behaviour.
- Tycho Brahe observes stars, Johannes Keper recognizes regularities, and learns to predict planetary motion.
- Isaac Newton observes various models, recognizes regularities, and develops a general model of gravity.
- Computer observes handwritten characters, recognizes regularities, and learns to recognize characters.
- Computer observes your mailbox, recognizes regularities, and learns to filter spam.
- Computer observes natural language, recognizes regularities, and learns to translate.
- Computer observes biological data, recognizes regularities, and discovers novel biology.
Unexpectedly for us, we have stumbled upon a phenomemon, which, when implemented correctly, really "feels" like true intelligence. Hence, intelligence is not about logical inference nor extensive knowledge. It is all about the skill of recognizing regularities and patterns. Humans have evolved from preprogrammed cause-and-effect reflexes through simple "remembering" all the way towards fairly sophisticated pattern analysis. Computers now are following a similar path and are gradually joining us in The Game. There is still a long way to go, but we have a clear direction: The Intelligence, achieving which means basically "winning" The Game. If anything at all, this is the purpose of our existence - discovering all the regularities in the surrounding world for the sake of total domination of Nature. And we shall use the best intelligence we can craft to achieve it (unless we all die prematurely, of course, which would be sad, but someday some other species would appear to take a shot at the game).
Epilogue. Strong AI
There is a curious concept in the philosophical realms of computer science — "The Strong AI Hypothesis". It relates to the distinction between manufacturing "true consciousness" (so-called "strong AI") and creating "only a simulation of consciousness" (the "weak AI"). Although it is impossible to distinguish the two experimentally, there seems to be an emotional urge to make the distinction. This usually manifests in argumentation of the following kind: "System X is not true artificial intelligence, because it is a preprogrammed algorithm; Humans will never create true AI, because, unlike us, a preprogrammed algorithm will hever have free will; etc."
Despite the seemingly unscientific nature of the issue, there is a way to look at it rationally. It is probably true that we shall never admit "true intelligence" nor "consciousness" to anything which acts according to an algorithm which is, in some sense, predictable or understandable by us. On the other hand, every complex system that we ever create, has to be made according to clearly understandable blueprints. The proper way of phrasing the "Strong AI" question is therefore the following: is it possible to create a system, which is built according to "simple" blueprints, and yet the behaviour of which is beyond our comprehension.
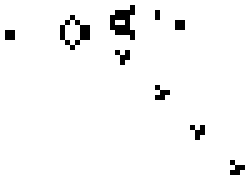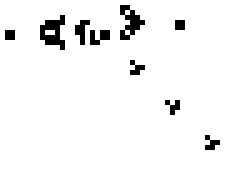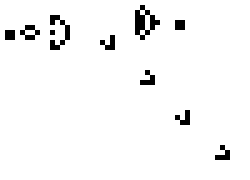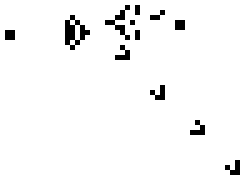
Cellular automaton
The answer to this question is not immediately clear, but my personal opinion is that it is a strong "yes". There are at least three kinds of approaches known nowadays, which provide a means for us to create something "smarter" than us. Firstly, using everything fractal, cellular, and generally chaotic is a simple recipe for producing uncomprehensibly complex behaviour from trivial rules. The problem with this approach, however, is that there is no good methodology for crafting any useful functions into a chaotic system.
The second candidate is anything neural — obviously the choice of Mother Nature. Neural networks have the same property of being able to demonstrate behaviour, which is not immediately obvious from the neurons or the connections among them. We know how to train some types of networks and we have living examples to be inspired by. Nonetheless, it is still hard to actually "program" neural networks. Hence, the third and the most promising approach — general machine learning and pattern recognition.
The idea of a pattern recognition-based system is to use a simple algorithm, accompanied by a huge dataset. Note that the distinction between the "algorithm" and the "dataset" here draws a clear boundary between two parts of a single system. The "algorithm" is the part which we need to understand and include in our "blueprints". The "data" is the remaining part, which we do not care knowing about. In fact, the data can be so vast, that no human is capable of grasping it completely. Collecting petabytes is no big deal these days any more. This is a perfect recipe for making a system which will be capable of demonstrating behaviour that would be unpredictable and "intelligent" enough for us to call it "free will".
Think of it...
![]() and the bias term
and the bias term ![]() . While the problem of finding
. While the problem of finding ![]() is typically explained in sufficient detail, the procedure of computing
is typically explained in sufficient detail, the procedure of computing ![]() is usually swept under the carpet.
is usually swept under the carpet.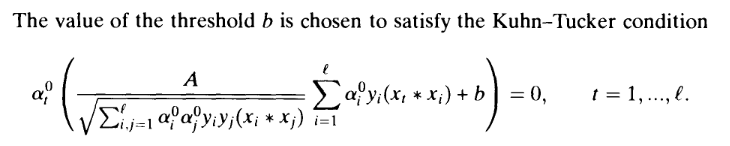 According to my calculations this is plain incorrect, because the corresponding Kuhn-Tucker conditions (in the "soft margin" SVM that we are considering here) are actually:
According to my calculations this is plain incorrect, because the corresponding Kuhn-Tucker conditions (in the "soft margin" SVM that we are considering here) are actually:![Rendered by QuickLaTeX.com \[\alpha_t^0\left(\frac{1}{\gamma}\sum_{i=1}^\ell \alpha_i^0y_i(x_t * x_i) + b-1+\xi_i\right) = 0\]](https://fouryears.eu/wp-content/ql-cache/quicklatex.com-307ccd09d2869e87f9bf8e43968fc587_l3.png)
![]() term, which is unknown, hence the equation is not useful for finding
term, which is unknown, hence the equation is not useful for finding ![]() . Later on, the reader is also presented with the following summarizing description of the algorithm:
. Later on, the reader is also presented with the following summarizing description of the algorithm: Do you see any mention of the way to compute
Do you see any mention of the way to compute ![]() ? I would expect the author to be somewhat more helpful with respect to this detail, which is obviously important for anyone willing to implement their own version of SVM.
? I would expect the author to be somewhat more helpful with respect to this detail, which is obviously important for anyone willing to implement their own version of SVM.![]() (Proposition 6.11, page 106):
(Proposition 6.11, page 106):![]() we need to find
we need to find ![]() , such that
, such that ![]() , i.e. there must exist at least one training point lying exactly on the margin. Although in most practical situations such support vectors will indeed exist, it is also theoretically possible that there won't be any, i.e. not a single support vector will lie exactly on the margin. Thus, for purposes of implementing SVMs, the provided specification is incomplete.
, i.e. there must exist at least one training point lying exactly on the margin. Although in most practical situations such support vectors will indeed exist, it is also theoretically possible that there won't be any, i.e. not a single support vector will lie exactly on the margin. Thus, for purposes of implementing SVMs, the provided specification is incomplete.![]() we need to choose
we need to choose ![]() such that the corresponding
such that the corresponding ![]() are strictly between 0 and
are strictly between 0 and ![]() . This is not necessarily true for any
. This is not necessarily true for any ![]() .
.![]() ? Of course, it is not too hard to derive, and thus makes for a great course homework exercise (e.g. Exercise 4 here). If you managed to read up to this point, I presume you should be motivated enough to try solving it. If you give up, you are welcome to consult my sample solution (Exercise 4, page 7).
? Of course, it is not too hard to derive, and thus makes for a great course homework exercise (e.g. Exercise 4 here). If you managed to read up to this point, I presume you should be motivated enough to try solving it. If you give up, you are welcome to consult my sample solution (Exercise 4, page 7).