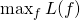Probability theory is often used as a sound mathematical foundation to formalize and derive solutions to the real-life problems in fields such as game theory, decision theory or theoretical economics. However, it often turns out that the somewhat simplistic "traditional" probabilistic approach is insufficient to formalize the real world, and this results in a large number of rather curious paradoxes.
One of my favourite examples is the Ellsberg's paradox, which goes as follows. Imagine that you are presented with an urn, containing 3 white balls and 5 other balls, that can be gray or black (but you don't know how many of these 5 exactly are gray, and how many are black). You will now draw one ball from the urn at random, and you have to choose between one of the two gambles:
- 1A)
- You win if you draw a white ball.
- 1B)
- You win if you draw a black ball.
Which one would you prefer to play? Next, imagine the same urn with the same balls, but the following choice of gambles:
- 2A)
- You win if you draw either a white or a gray ball.
- 2B)
- You win if you draw either a black or a gray ball.
The paradox lies in the fact, that most people would strictly prefer 1A to 1B, and 2B to 2A, which seems illogical. Indeed, let the number of white balls be W=3, the number of gray balls be G and the number of black balls - B. If you prefer 1A to 1B, you seem to be presuming that W > B. But then W+G > B+G and you should necessarily also be preferring 2A to 2B.
What is the problem here? Of course, the problem lies in the uncertainty behind the number of black balls. We know absolutely nothing about it, and we have to guess. Putting it in Bayesian terms, in order to make a decision we have specify our prior belief in what is the probability that there would be 0, 1, 2, 3, 4 or 5 black balls in the urn. The classical way of modeling the "complete uncertainty" would be to state that all the options are equiprobable. In this case the probability of having more black balls in the urn than the white balls is only 2/6 (this can happen when there are 4 or 5 black balls, each option having probability 1/6), and it is therefore reasonable to bet on the whites. We should therefore prefer 1A to 1B and 2A to 2B.
The real life, however, demonstrates that the above logic does not adequately describe how most people decide in practice. The reason is that we would not assign equal probabilities to the presumed number of black balls in the urn. Moreover, in the two situations our prior beliefs would differ, and there is a good reason for that.
If the whole game were real, there would be someone who had proposed it to us in the first place. This someone was also responsible for the number of black balls in the urn. If we knew who this person was, we could base our prior belief on our knowledge of that person's motives and character traits. Is he a kindhearted person who wants us to win, or is he an evil adversary who would do everything to make us lose? In our situation we don't know, and we have to guess. Would it be natural to presume the uncertainty to be a kindhearted friend? No, for at least the following reasons:
- If the initiator of the game is not a complete idiot, he would aim at gaining something from it, or why would he arrange the game in the first place?
- If we bet on the kindness of the opponent we can lose a lot when mistaken. If, on the contrary, we presume the opponent to be evil rather than kind, we are choosing a more robust solution: it will also work fine for the kind opponent.
Therefore, it is natural to regard any such game as being played against an adversary and skew our prior beliefs to the safer, more robust side. The statement of the problem does not clearly require the adversary to select the same number of black balls for the two situations. Thus, depending on the setting, the safe side may be different. Now it becomes clear why in the first case it is reasonable to presume that the number of black balls is probably less than the number of white balls: this is the only way the adversary can make our life more difficult. In the second case, the adversary would prefer the contrary: a larger number of black balls. Therefore, we would be better off reversing our preferences. This, it seems to me, explains the above paradox and also nicely illustrates how the popular way of modeling total uncertainty using a uniform prior irrespective of the context fails to consider the real-life common sense biases.
The somewhat strange issue remains, however. If you now rephrase the original problem more precisely and define that the number of black balls is uniformly distributed, many people will still intuitively tend to prefer 2B over 2A. One reason for that is philosophical: we might believe that the game with a uniform prior on the black balls is so unrealistic, that we shall never really have the chance to take a decision in such a setting. Thus, there is nothing wrong in providing a "wrong" answer for this case, and it is still reasonable to prefer the "wrong" decision because in practice it is more robust. Secondly, I think most people never really grasp the notion of true uniform randomness. Intuitively, the odds are always against us.
Appendix
There are still a pair of subtleties behind the Ellsberg's problem, which might be of limited interest to you, but I find the discussion somewhat incomplete without them. Read on if really want to get bored.
Namely, what if we especially stress, that you have to play both games, and both of them from the same urn? Note that in this case the paradox is not that obvious any more: you will probably think twice before betting on white and black simultaneously. In fact, you'd probably base your decision on whether you wish to win at least one or rather both of the games. Secondly, what if we say that you play both games simultaneously by picking just one ball? This would provide an additional twist, as we shall see in a moment.
I. Two independent games
So first of all, consider the setting where you have one urn, and you play two games by drawing two balls with replacement. Consider two goals: winning at least one of the two games, and winning both.
I-a) Winning at least one game
To undestand the problem we compute the probabilities of winning game 1A, 1B, 2A, 2B for different numbers of black balls, and then the probabilities of winning at least one of two games for our different choices:
| Black balls |
Probability of winning a gamble |
Probability of winning one of two gambles |
| 1A |
1B |
2A |
2B |
1A or 2A |
1A or 2B |
1B or 2A |
1B or 2B |
| 0 |
3/8 |
0/8 |
8/8 |
5/8 |
1 |
39/64 |
1 |
40/64 |
| 1 |
3/8 |
1/8 |
7/8 |
5/8 |
59/64 |
39/64 |
57/64 |
43/64 |
| 2 |
3/8 |
2/8 |
6/8 |
5/8 |
54/64 |
39/64 |
52/64 |
46/64 |
| 3 |
3/8 |
3/8 |
5/8 |
5/8 |
49/64 |
39/64 |
39/64 |
49/64 |
| 4 |
3/8 |
4/8 |
4/8 |
5/8 |
44/64 |
39/64 |
38/64 |
52/64 |
| 5 |
3/8 |
5/8 |
3/8 |
5/8 |
39/64 |
39/64 |
39/64 |
55/64 |
Probabilities of winning various gambles for different numbers of black balls
Now the problem can be regarded as a classical game between us and "the odds": we want to maximize our probabilities by choosing the gamble correctly, and "the odds" wants to minimize our chances by providing us with a bad number of black balls. The game presented above has no Nash equilibrium, but it seems that the choice of 3 black balls is the worst for us on average. And if we follow this pessimistic assumption, we see that the correct choice would be to pick consistently either both "A" or both "B" gambles (a further look suggests that both "A"-s is probably the better choice of the two).
I-b) Winning two games
Next, assume that we really need to win both of the games. The following table summarizes our options:
| Black balls |
Probability of winning a gamble |
Probability of winning two gambles |
| 1A |
1B |
2A |
2B |
1A and 2A |
1A and 2B |
1B and 2A |
1B and 2B |
| 0 |
3/8 |
0/8 |
8/8 |
5/8 |
24/64 |
15/64 |
0 |
0 |
| 1 |
3/8 |
1/8 |
7/8 |
5/8 |
21/64 |
15/64 |
7/64 |
5/64 |
| 2 |
3/8 |
2/8 |
6/8 |
5/8 |
18/64 |
15/64 |
12/64 |
10/64 |
| 3 |
3/8 |
3/8 |
5/8 |
5/8 |
15/64 |
15/64 |
15/64 |
15/64 |
| 4 |
3/8 |
4/8 |
4/8 |
5/8 |
12/64 |
15/64 |
16/64 |
20/64 |
| 5 |
3/8 |
5/8 |
3/8 |
5/8 |
9/64 |
15/64 |
15/64 |
25/64 |
Probabilities of winning various gambles for different numbers of black balls
This game actually has a Nash equilibrium, realized when we select options 1A and 2B. Remarkably, it corresponds exactly to the claim of the paradox: when we need to win both games and are pessimistic about the odds, we should prefer the options with the least amount of uncertainty.
II. Two dependent games
Finally, what if both games are played simultaneously by taking just one ball from the urn. In this case we also have two versions: aiming to win at least one, or aiming to win both games.
II-a) Winning at least one game
The solution here is to choose either the 1A-2B or the 1B-2A version, which always guarantees exactly one win. Indeed, if you pick a white ball, you win 1A, and otherwise you win 2B. The game matrix is the following:
| Black balls |
Probability of winning a gamble |
Probability of winning one of two gambles |
| 1A |
1B |
2A |
2B |
1A or 2A |
1A or 2B |
1B or 2A |
1B or 2B |
| 0 |
3/8 |
0/8 |
8/8 |
5/8 |
1 |
1 |
1 |
5/8 |
| 1 |
3/8 |
1/8 |
7/8 |
5/8 |
7/8 |
1 |
1 |
5/8 |
| 2 |
3/8 |
2/8 |
6/8 |
5/8 |
6/8 |
1 |
1 |
5/8 |
| 3 |
3/8 |
3/8 |
5/8 |
5/8 |
5/8 |
1 |
1 |
5/8 |
| 4 |
3/8 |
4/8 |
4/8 |
5/8 |
4/8 |
1 |
1 |
5/8 |
| 5 |
3/8 |
5/8 |
3/8 |
5/8 |
3/8 |
1 |
1 |
5/8 |
Probabilities of winning various gambles for different numbers of black balls
II-b) Winning both games
The game matrix looks as follows:
| Black balls |
Probability of winning a gamble |
Probability of winning two gambles |
| 1A |
1B |
2A |
2B |
1A and 2A |
1A and 2B |
1B and 2A |
1B and 2B |
| 0 |
3/8 |
0/8 |
8/8 |
5/8 |
3/8 |
0 |
0 |
0 |
| 1 |
3/8 |
1/8 |
7/8 |
5/8 |
3/8 |
0 |
0 |
1/8 |
| 2 |
3/8 |
2/8 |
6/8 |
5/8 |
3/8 |
0 |
0 |
2/8 |
| 3 |
3/8 |
3/8 |
5/8 |
5/8 |
3/8 |
0 |
0 |
3/8 |
| 4 |
3/8 |
4/8 |
4/8 |
5/8 |
3/8 |
0 |
0 |
4/8 |
| 5 |
3/8 |
5/8 |
3/8 |
5/8 |
3/8 |
0 |
0 |
5/8 |
Probabilities of winning various gambles for different numbers of black balls
The situation here is contrary to the previous: if you win 1A, you necessarily lose 2B, so here you have to bet both "A"-s to achieve a Nash equilibrium.
Summary
If you managed to read to this point, then I hope you've got the main idea, but let me summarize it once more: the main "problem" with the Ellsberg's paradox (as well as a number of other similar paradoxes) can be in part due to the fact that pure "uniform-prior" probability theory is not the correct way to approach game-theoretical problems, as it tends to hide from view a number of aspects that we, as humans, usually handle nearly subconsciously.
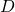 denote the dataset, let
denote the dataset, let  be the pattern space (e.g. "the space of all sequences", or "the space of all classifiers", etc), and let for each
be the pattern space (e.g. "the space of all sequences", or "the space of all classifiers", etc), and let for each 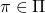 there be a pattern function
there be a pattern function 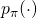 , so that
, so that 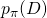 measures the "interestingness" of this pattern with respect to the data
measures the "interestingness" of this pattern with respect to the data 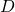 . Then the general task of pattern analysis is just the following maximization problem:
. Then the general task of pattern analysis is just the following maximization problem:

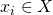 , and the task is to find a function
, and the task is to find a function 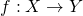 that maps these instances to corresponding "outputs"
that maps these instances to corresponding "outputs" 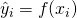 in various ways.
in various ways.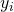 is provided with each instance
is provided with each instance 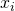 , and the resulting function should aim to match this output for given instances (i.e.
, and the resulting function should aim to match this output for given instances (i.e. 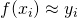 ) as well as generalize to the unseen ones. Statisticians call this task regression analysis. A classical example is the problem of detecting incoming spam mail by learning the classification rule from previously labeled messages.
) as well as generalize to the unseen ones. Statisticians call this task regression analysis. A classical example is the problem of detecting incoming spam mail by learning the classification rule from previously labeled messages. without any prespecified labeling of data. Typically one searches for a function that maps similar inputs to similar outputs. If the set of outputs
without any prespecified labeling of data. Typically one searches for a function that maps similar inputs to similar outputs. If the set of outputs  is small and discrete, the task is referred to as clustering and somewhat resembles the problem of quantization. If the outputs are continuous, the task can often be related to either factor analysis or noise reduction.
is small and discrete, the task is referred to as clustering and somewhat resembles the problem of quantization. If the outputs are continuous, the task can often be related to either factor analysis or noise reduction.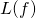 , that estimates the goodness of fit for a given classifier
, that estimates the goodness of fit for a given classifier 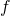 , and then searching for a classifier that optimizes this measure, i.e.:
, and then searching for a classifier that optimizes this measure, i.e.: