Four Years Remaining

Ever since Erwin Schrödinger described a thought experiment, in which a cat in a sealed box happened to be "both dead and alive at the same time", popular science writers have been relying on it heavily to convey the mysteries of quantum physics to the layman. Unfortunately, instead of providing any useful intuition, this example has instead laid solid base to a whole bunch of misconceptions. Having read or heard something about the strange cat, people would tend to jump to profound conclusions, such as "according to quantum physics, cats can be both dead and alive at the same time" or "the notion of a conscious observer is important in quantum physics". All of these are wrong, as is the image of a cat, who is "both dead and alive at the same time". The corresponding Wikipedia page does not stress this fact well enough, hence I thought the Internet might benefit from a yet another explanatory post.

The Story of the Cat

The basic notion in quantum mechanics is a quantum system. Pretty much anything could be modeled as a quantum system, but the most common examples are elementary particles, such as electrons or photons. A quantum system is described by its state. For example, a photon has polarization, which could be vertical or horizontal. Another prominent example of a particle's state is its wave function, which represents its position in space.

There is nothing special about saying that things have state. For example, we may say that any cat has a "liveness state", because it can be either "dead" or "alive". In quantum mechanics we would denote these basic states using the bra-ket notation as and . The strange thing about quantum mechanical systems, though, is the fact that quantum states can be combined together to form superpositions. Not only could a photon have a purely vertical polarization  or a purely horizontal polarization , but it could also be in a superposition of both vertical and horizontal states:

This means that if you asked the question "is this photon polarized vertically?", you would get a positive answer with 50% probability - in another 50% of cases the measurement would report the photon as horizontally-polarized. This is not, however, the same kind of uncertainty that you get from flipping a coin. The photon is not either horizontally or vertically polarized. It is both at the same time.

Amazed by this property of quantum systems, Schrödinger attempted to construct an example, where a domestic cat could be considered to be in the state

which means being both dead and alive at the same time. The example he came up with, in his own words (citing from Wikipedia), is the following:

A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny bit of radioactive substance, so small, that perhaps in the course of the hour one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube discharges and through a relay releases a hammer that shatters a small flask of hydrocyanic acid. If one has left this entire system to itself for an hour, one would say that the cat still lives if meanwhile no atom has decayed. The first atomic decay would have poisoned it.

The idea is that after an hour of waiting, the radiactive substance must be in the state

the poison flask should thus be in the state

and the cat, consequently, should be

Correct, right? No.

The Cat Ensemble

Superposition, which is being "in both states at once" is not the only type of uncertainty possible in quantum mechanics. There is also the "usual" kind of uncertainty, where a particle is in either of two states, we just do not exactly know which one. For example, if we measure the polarization of a photon, which was originally in the superposition , there is a 50% chance the photon will end up in the state  after the measurement, and a 50% chance the resulting state will be . If we do the measurement, but do not look at the outcome, we know that the resulting state of the photon must be either of the two options. It is not a superposition anymore. Instead, the corresponding situation is described by a statistical ensemble:

Although it may seem that the difference between a superposition and a statistical ensemble is a matter of terminology, it is not. The two situations are truly different and can be distinguished experimentally. Essentially, every time a quantum system is measured (which happens, among other things, every time it interacts with a non-quantum system) all the quantum superpositions are "converted" to ensembles - concepts native to the non-quantum world. This process is sometimes referred to as decoherence.

Now recall the Schrödinger's cat. For the cat to die, a Geiger counter must register a decay event, triggering a killing procedure. The registration within the Geiger counter is effectively an act of measurement, which will, of course, "convert" the superposition state into a statistical ensemble, just like in the case of a photon which we just measured without looking at the outcome. Consequently, the poison flask will never be in a superposition of being "both broken and not". It will be either, just like any non-quantum object should. Similarly, the cat will also end up being either dead or alive - you just cannot know exactly which option it is before you peek into the box. Nothing special or quantum'y about this.

The Quantum Cat

"But what gives us the right to claim that the Geiger counter, the flask and the cat in the box are "non-quantum" objects?", an attentive reader might ask here. Could we imagine that everything, including the cat, is a quantum system, so that no actual measurement or decoherence would happen inside the box? Could the cat be "both dead and alive" then?

Indeed, we could try to model the cat as a quantum system with and being its basis states. In this case the cat indeed could end up in the state of being both dead and alive. However, this would not be its most exciting capability. Way more suprisingly, we could then kill and revive our cat at will, back and forth, by simply measuring its liveness state appropriately. It is easy to see how this model is unrepresentative of real cats in general, and the worry about them being able to be in superposition is just one of the many inconsistencies. The same goes for the flask and the Geiger counter, which, if considered to be quantum systems, get the magical abilities to "break" and "un-break", "measure" and "un-measure" particles at will. Those would certainly not be a real world flask nor a counter anymore.

The Cat Multiverse

There is one way to bring quantum superposition back into the picture, although it requires some rather abstract thinking. There is a theorem in quantum mechanics, which states that any statistical ensemble can be regarded as a partial view of a higher-dimensional superposition. Let us see what this means. Consider a (non-quantum) Schrödinger's cat. As it might be hopefully clear from the explanations above, the cat must be either dead or alive (not both), and we may formally represent this as a statistical ensemble:

It turns out that this ensemble is mathematically equivalent in all respects to a superposition state of a higher order:

where "Universe A" and "Universe B" are some abstract, unobservable "states of the world". The situation can be interpreted by imagining two parallel universes: one where the cat is dead and one where it is alive. These universes exist simultaneously in a superposition, and we are present in both of them at the same time, until we open the box. When we do, the universe superposition collapses to a single choice of the two options and we are presented with either a dead, or a live cat.

Yet, although the universes happen to be in a superposition here, existing both at the same time, the cat itself remains completely ordinary, being either totally dead or fully alive, depending on the chosen universe. The Schrödinger's cat is just a cat, after all.

Ever since the "Prior Confusion" post I was planning to formulate one of its paragraphs as the following abstract puzzle, but somehow it took me 8 years to write it up.

According to fictional statistical studies, the following is known about a fictional chronic disease "statistite":

1. About 30% of people in the world have statistite.
2. About 35% of men in the world have it.
3. In Estonia, 20% of people have statistite.
4. Out of people younger than 20 years, just 5% have the disease.
5. A recent study of a random sample of visitors to the Central Hospital demonstrated that 40% of them suffer from statistite.

Mart, a 19-year Estonian male medical student is standing in the foyer of the Central Hospital, reading these facts from an information sheet and wondering: what are his current chances of having statistite? How should he model himself: should he consider himself as primarily "an average man", "a typical Estonian", "just a young person", or "an average visitor of the hospital"? Could he combine the different aspects of his personality to make better use of the available information? How? In general, what would be the best possible probability estimate, given the data?

Research and engineering always go hand in hand. Their relationship is so tight that often people cease to see the difference. Indeed, both are development activities that bring along technical advances. Many researchers work in engineering companies, many engineers do what is essentially research, is there even a need to see the difference? Quite often there is. Let me highlight this difference.

Research (sometimes synonymous with "science") is, ideally, an experimental activity, which aims to explore some space of possibilities in order to hopefully come up with a certain "understanding" of what those possibilities are or how they should be used. Researchers primarily deliver written reports, summarizing their findings. There is absolutely no guarantee that those findings would be "interesting" or "useful" to any degree - indeed, a research project by definition starts off in a position of uncertainty. As a result, for practical, commercial or investment purposes, research is always a risky activity. It may take a long time, it will produce mostly text, and there is no guarantee that the results will be of use. The upside of this risk is, of course, the chance to stumble upon unique innovation, which may eventually bring considerable benefits. Later.

Engineering is a construction activity, where existing knowledge and tools are put together to deliver actual products. In order for this process to be successful, experimentation and uncertainty must be, ideally, brought down to a minimum. Thus, when compared to pure research, engineering projects are low risk endeavors, where the expected outputs are known in advance.

In simple terms - researchers answer questions whilst engineers build things, and by this definition those occupations are, obviously, very different. This difference is often apparent in material fields, such as construction or electronics, where the engineers can be distinguished from the researchers by the kind of tools they would mostly hold in their hands and the places they would spend their time the most. With computational fields this visual difference does not exist - both engineers and researchers spend most of their time behind a computer screen. The tools and approaches are still different, but you won't spot this unless you are in the field. I did not know the difference between Software Engineering and Computer Science until I had the chance to try both.

Things become even more confusing when data mining gets involved. The popularity of projects, which focus on building data-driven intelligent systems, is ever growing. As a result, more and more companies seem to be eager to embrace this magical world by hiring "data scientists" to do "data science" for them. The irony of the situation is that most of those companies are engineering businesses (e.g. software developer firms) and, as such, they would not (or at least should not) normally consider hiring anyone with the word "scientist" in the job title. Because scientists are not too famous for bringing stable income, engineers are.

The term "data science" is a vague one, but I think it is quite succinct in that it captures the exploratory aspect that is inherent in general-purpose data analysis, as well as the current state of the art in the field. Although there are some good high level tools for a wide range of "simple" machine learning tasks nowadays, as soon as you want to try something more exotic, you are often on your own, faced with uncertainty and the need to experiment before you can even try to "build" anything. For a typical engineering company such uncertainty is not a good thing to rely upon.

It does not mean that one cannot engineer data-driven systems nowadays, it means that in reality most of the companies, whether they know it or not, need a very particular kind of "data scientists". They need specialists with a good knowledge of simple reliable tools and are capable of applying them to various data formats. Those, who would perhaps avoid excessive experimentation in favor of simple, scalable, working solutions, even if those are somehow simplistic, suboptimal and do not employ custom-designed forty-layer convolutional networks with inception blocks, which require several months to debug and train. Those, who might not know much about concentration inequalities but would be fluent in data warehousing and streaming. There's actually a name for such people: "Data engineers".

There is nothing novel about the use of such terminology, yet I still regularly encounter way too much misunderstanding around this topic over and over again.

In particular, I would expect way more of the "Data engineering" curricula to appear at universities alongside the more or less standard "Data science" ones. The difference between the two would be slight, but notable - pretty much of the same order as the difference between our "Computer science" and "Software engineering" master's programmes, for example.

Most results that are published in mathematics and natural sciences are highly technical and obscure to anyone outside the particular area of research. Consequently, most scientific publications and discoveries do not get any media attention at all. This is a problem both for the public (which would benefit from knowing a bit more about our world), the science in general (which would benefit from wider dissemination) and the scientists themselves (which would certainly appreciate if their work reached more than a couple of other people). The issue is usually addressed by the researchers trying to popularize their findings — provide simple interpretations, which could be grasped by the layman without the need to understand the foundations. Unfortunately, if the researcher was lucky to grab enough media attention, chances are high the process of "popularization" will get completely out of hands, and the message received by the public will have nothing to do with the original finding.

There are some theorems in pure mathematics, which happened to suffer especially seriously from this phenomenon. My two most favourite examples are the Heizenberg's uncertainty principle and Gödel's incompleteness theorems. Every once in a while I stumble on pieces, written by people who have zero knowledge of basic physics (not even mentioning quantum mechanics or Fourier theory), but claim to have clearly understood the meaning and the deep implications of the uncertainty principle upon our daily lives. Even more popular are Gödel's theorems. "Science proves that some things in this world can never be understood or predicted by us, mere humans!!!" is a typical take on Gödel by the press. Oh, and it is loved by religion enthusiasts!

This post is my desperate attempt to bring some sanity back into this world by providing a (yet another, but maybe slightly different) popular explanation for Gödel's ideas.

Gödel's theorems explained (with enough context)

Kurt Gödel

In our daily lives we primarily use symbols to communicate and describe the world. Those may be formulas in mathematics or simply sentences in the English language. Symbol-based systems can be used in different ways. From the perspective of arts and humanities, one is welcome to construct arbitrary sequences of words and sentences, as long as the result is "beautiful", "inspiring" or "seems smart and convincing". From a more technically-minded point of view, however, one is only welcome to operate with "true and logical" statements. However, it is not at all obvious which statements should be universally considered "true and logical". There are two ways the problem can be resolved.

Firstly, we can determine the truth by consulting "reality". For example, the phrase "All people are mortal, hence Socrates is mortal" is true because, indeed (avoiding a lecture-worth of formalities or so), in all possible universes where there are people and they are mortal, Socrates will always also be mortal.

Secondly, we can simply postulate a set of statements, which we shall universally regard as "the true ones". To distinguish those postulated truths from the "actual truths", mentioned in the paragraph above, let us call them "logically correct statements". That is, we can hypothetically write down an (infinite) list of all the "logically correct" sentences in some hypothetical "Book of All Logically Correct Statements". From that time on, every claim not in the book will be deemed "illogical" and hence "false" (the question of whether it is false in reality would, of course, depend on the goodness and relevance of the book we created).

This is really convenient, because now in order to check the correctness of the claim about Socrates we do not have to actually visit all the possible universes. It suffices to look it up in our book! If the book is any good, it will provide good answers, so the concept of "logical correctness" may be close or even equivalent to "actual truth". And in principle, there must exist "The Actual Book of Truth", which would list precisely the "actually true" statements.

Unfortunately, infinite books are somewhat inconvenient to print and carry around. Luckily, we can try to represent an infinite book in a finite way using algorithms. We have all seen how a short algorithm is capable of producing an infinite amount of nonsense, haven't we? Thus, instead of looking for an (infinitely-sized) "book of truth", we should look for a (finitely-sized) "algorithm of truth", which will be either capable of generating the whole book, or checking for any given statement, whether it belongs to the book.

Frege's propositional calculus

For clarity and historical reasons,  the algorithms for describing "books of truths" are usually developed and written down using a particular "programming language", which consists of "axioms" and "inference rules". Here is one of the simplest examples of how a "program" might look like.

This is where a natural question arises: even if we assume that we have access to "the actual book of truth", will it really be possible to compress it down to a finite algorithm? Isn't it too much to ask? It turns out it is. There is really no way to create a compact representation for any but the most trivial "books of truths".

Besides the "asking too much" intuition, there are at least two other simple reasons why this is impossible. Firstly, most of the readers here know that there exist problems, that are in principle uncomputable. Those are usually about statements, the correctness of which cannot be checked in finite time by a finite algorithm, with the most famous example being the halting problem, as well as everything related to uncomputable numbers.

Naturally, if we can't even use a finite algorithm to list "all truly halting programs", our hopes for getting a finite description for any more complicated "book of truths" is gone. But there is another funny reason. Once we have decided to define the book with all true statements and devise an algorithm for generating it, we must not forget to include into the book some statements about the book and the algorithm themselves. In particular, we must consider the following phrase: "This sentence will not be included in the book generated by our algorithm."

If our algorithm does include this sentence in the generated book, the claim turns out to be false. As a result, our precious book would have false statements in it: it would be inconsistent. On the other hand, if our algorithm produces a book which does not include the above sentence, the sentence turns out to be true and the book is incomplete. It is just the liar's paradox.

And so it is — we have to put up with the situation, where it is impossible to produce a finite representation for all true statements without stumbling into logical paradoxes. Or, alternatively, that there are mathematical statements, which cannot be checked or proven within a finite time.

This describes what is known as "Gödel's first incompleteness theorem" (namely, the claim that in most cases our algorithm is only capable of producing either an incomplete or an inconsistent "book"). A curious corollary may be derived from it, which is known as the "Gödel's second incompleteness theorem". The theorem says that if our "book-generating algorithm" happens to include into it exactly the phrase "This book is consistent", it must necessarily be a false claim, and the algorithm must actually be inconsistent. This is often interpreted that no "honest" theory is capable of claiming it's own correctness (there are caveats, though).

Gödel's theorems have several interesting implications for the foundations of mathematics. None the less, those are still theorems about the fundamental impossibility of using a finite algorithm for generating a book of logically correct statements without stumbling into logical paradoxes and infinite loops. Nothing more and nothing less. They have nothing to do with the experimental sciences: note how we had to cut away all connections to reality in the very first paragraphs of the explanation. And thus, Gödel's theorems are not related to the causes of "human inability to grasp the universe", "failure or success of startup business plans", or anything else of that kind.

It seems to be popular among some of my (very scientifically-minded) friends to somewhat provocatively defend a claim, that "fundamentally, there is no difference between a scientific worldview and a superstitious or a religious one". The typical justification is that the desire of one person to believe the scientific methodology and only trust in the "material world" has the same roots as the desire of another person to believe in the supernatural. Consequently, it should be unfair to claim that one set of beliefs must have a priority over the other. In the words of a well-versed narrator, this line of argument can be made very convincing and leave one wondering: if the choice of basic beliefs is indeed just a matter of taste and cultural traditions, why does it still seem that the "scientific worldview" is somewhat more "practical". Is it just an illusion? The following is an attempt to justify that it is not, and that there are some simple reasons for the objectivist worldview to be superior.

In order to avoid misunderstanding, so common in philosophical discourses, we must start by defining some very basic terms.

• First, an obvious yet necessary definition of us. By "us" I mean just myself and you, the reader. The existence of me requires no proof for me and I presume this is symmetric with you. The existence of you I can observe personally when we have a chance to meet. Thus, we might agree there is this thing called "us".
• By a subjective reality I mean everything perceivable by me. This, again, requires no proof for me. I presume that there is an equivalent subjective reality for you. Most importantly, although our two realities may not necessarily be equal, they have a lot of things in common. For example, the text of this post obviously belongs to both. Thus, the set of things shared by our subjective realities shall be referred to as (our) objective reality.
• By an individual we shall mean some entity, capable of communicating with us. That is, an individual is something capable of perceiving our signals and reacting to them. We do not assume any other properties for an individual - it may be a person, a fairy, or an alien. As long as we can communicate in some way, it fits the definition.
• By an individual's worldview we shall regard the set of all the possible reactions of an individual to all the possible stimuli. That is, I declare the individual's worldview to be exactly defined by its observable behaviour. In order for two individuals to have differing worldviews they must behave (or, to be more precise, communicate) differently in at least one situation.

Communication can take multiple forms. Let us limit ourselves mainly with verbal communication. Consideration of nonverbal worldviews would complicate the discussion for no good reason (those would be things such as musical and culinary tastes).

So, suppose we have an individual. We can talk to it, and it can answer something. Its worldview is then just the set of answers to the questions in a given context (-Do fairies exist? -Yes/No/I don't know; -Is this liquid poisonous? -Yes/No/I don't know; etc).

Obviously, according to such a definition, every person in this world is an individual and has its own unique worldview. The worldviews of some people are perhaps "more scientific" and those of others are perhaps "more superstitious". In the following I am going to show that there is one worldview which is "most informative" for the purposes of our communication with that individual, and this will be precisely the "scientific" one.

• By a basic stimulus we shall call a stimulus, to which an individual responds in a way which is reproducible to some extent. Any other stimuli (those that provide a purely random response) are essentially uninformative and we would have no use for them in communication with the individual. The simplest example of a basic stimulus is a constant response. For example, most normal people, when pointed to a glass of milk and asked "Is this milk?", should provide a reproducible answer "Yes". Thus, "Is this milk?" is a basic stimulus.
• Next, we shall say that the basic stimulus is objective, if there is at least some observable property of (our) objective reality, changing which would (again, reproducibly) influence the reaction to that stimulus. Any non-objective stimuli are of no interest to us, because they bear no relation to observable objective reality, and thus we have no way of interpreting the answer.
  For example, an individual might constantly respond "Boo!" to a query-phrase "Baa?", which means that "Baa?" a basic stimulus. However, we have no way of associating the answer "Boo!" with anything material, and thus have no way of understanding this response. Hence, from the point of view of communication, the query "Baa?" makes no sense. Similarly, if a person answers to the question "Do fairies exist" by "No", no matter what, we shall call this question non-objective.

Now that we are done with the preliminary definitions, let me state the main claims.

• We say that a worldview is ideally scientific, if it has the maximum possible set of basic objective stimuli (and any reactions to them).

Most probably no human has an ideally scientific worldview simply because no human has explored all of the quirks of our objective reality. But each individual's worldview can be regarded as more or less scientific considering the amount of its basic objective stimuli. Contrarily,

• We say that a worldview is ideally dogmatic, if it has the maximum possible set of basic non-objective stimuli.

An ideally dogmatic worldview is, of course, meaningless, as it basically means that it has a fixed response to any question. However, we can say that each person's worldview has it's own degree of dogmaticity.

Here lies the answer to the difference between a "scientific" and a "superstitious" (i.e. dogmatic or religious) worldviews. The former one is the only worldview, which makes sense for establishing communication between individuals (irrespectively of what "realities" each of them might live or believe in). This is the reason, which sets such a worldview forth as the "practical" one.

It is important to understand that, in principle, there is nothing in this exposition that excludes the possibility for some people to actually have "their own" part of reality. For example, if person X tells me that he sees little green men all around, it may very well be something truly objective in his part of reality, which is, for some reason, not shared with me. Consequently, I will have to regard his statement as non-objective and as long as I do so, such a statement will be useless for communication and thus non-scientific (for the reality, which includes me and person X). I will thus say to him: "I do not refuse to believe in you seeing those little green men, but as long as I myself cannot observe their existence, discussing them with me is non-scientific, i.e. uninformative".

This is a (slightly modified) write-up of a part of a lecture I did for the "Welcome to Computer Science" course last semester.

Part I. Humans Discover the World

How it all started

Millions of years ago humans were basically monkeys. Our ape-like ancestors enjoyed a happy existence in the great wide world of Nature. Their life was simple, their minds were devoid of thought, and their actions were guided by simple cause-and-effect mechanisms. Although for a modern human it might seem somewhat counterintuitive or even hard to imagine, the ability to think or understand is, in fact, completely unnecessary to succesfully survive in this world. As long as a living creature knows how to properly react to the various external stimuli, it will do just fine. When an ape sees something scary — ape runs. When an ape seems something tasty — ape eats. When an ape sees another ape — ape acts according to whatever action pattern is wired into its neural circuits. Does the ape understand what is happening and make choices? Not really — it is all about rather basic cause and effect.

As time went by, evolution blessed our ape-like ancestors with some extra brain tissue. Now they could develop more complicated reaction mechanisms and, in particular, they started to remember things. Note that, in my terminology here, "remembering" is not the same as "learning". Learning is about simple adaptation. For example, an animal can learn that a particular muscle movement is necessary to get up on a tree — a couple of failed attempts will rewire its neural circuit to perform this action as necessary. One does not even need a brain to learn — the concentration of proteins in a bacteria will adjust to fit the particular environment, essentially demonstrating a learning ability. "Remembering", however, requires some analytical processing.

Remembering

It is easy to learn to flex a particular finger muscle whenever you feel like climbing up a tree, but it is a totally different matter to actually note that you happen to regularly perform this action somewhy. It is even more complicated to see that the same finger action is performed both when you climb a tree and when you pick a banana. Recognizing such analogies between actions and events is not plain "learning" any more. It is not about fine-tuning the way a particular cause-and-effect reflex is working. It is a kind of information processing. As such, it requires a certain amount of "memory" to store information about previous actions and some pattern analysis capability to be able to detect similarities, analogies and patterns in the stored observations. Those are precisely the functions that were taken over by the "extra" brain tissue.

So, the apes started "remembering", noticing analogies and making generalization. Once the concept of "grabbing" is recognized as a recurring pattern, the idea of grabbing a stone instead of a tree branch is not far away. Further development of the brain lead to better "remembering" capabilities, more and more patterns discovered in the surrounding world, which eventually lead to the birth of symbolic processing in our brains.

Symbols

What is "grabbing"? It is an abstract notion, a recurring pattern, recognized by one of our brain circuits. The fact that we have this particular circuit allows us to recognize further occurrences of "grabbing" and generalize this idea in numerous ways. Hence, "grabbing" is just a symbol, a neural entity that helps our brains to describe a particular regularity in our lives.

As time went by, prehistoric humans became aware (or, let me say "became conscious") of more and more patterns, and developed more symbols. More symbols meant better awareness of the surrounding world and its capabilities (hence, the development of tools), more elaborate communication abilities (hence, the birth of language), and, recursively, better analytic abilities (because using symbols, you can search for patterns among patterns).

Symbols are immensely useful. Symbols are our way of being aware of the world, our way of controlling this world, our way of living in this world. The best thing about them is that they are easily spread. It may have taken centuries of human analytical power to note how the Sun moves along the sky, and how a shadow can be used to track time. But once this pattern has been discovered, it can be recorded and used infinitely. We are then free to go searching for other new exciting patterns. They are right in front of us, we just need to look hard. This makes up an awesome game for the humankind to play — find patterns, get rewards by gaining more control of the world, achieve better life quality, feel good, everyone wins! Not surprisingly, humans have been actively playing this game since the beginning of time. This game is what defines humankind, this is what drives its modern existence.

Science

Galelio's experiment

"All things fall down" — here's an apparently obvious pattern, which is always here, ready to be verified. And yet it took humankind many years to discover even its most basic properties. It seems that the europeans, at least, did not care much about this essential phenomenon until the XVIIth century. Only after going through millenia self-deception, followed by centuries of extensive aggression, devastating epidemics, and wild travels, the europeans found the time to sit down and just look around. This is when Galileo found out that, oh gosh, stuff falls down. Moreover, it does so with the same velocity independently of its size. In order to illustrate this astonishing fact he had to climb on to the tower of Pisa, throw steel balls down and measure the fall time using his own heartbeat.

In fact, the late Renaissance was most probably the time when europeans finally became aware of the game of science (after all, this is also a pattern that had to be discovered). People opened their eyes and started looking around. They understood that there are patterns waiting to be discovered. You couldn't see them well, and you had to look hard. Naturally, and somewhat ironically, the sky was the place they looked towards the most.

Patterns in the Sky

Tycho Brahe

Tycho Brahe, a contemporary of Galileo, was a rich nobleman. As many other rich noblemen of his time, he was excited about the sky and spent his nights as an astronomer. He truly believed there are patterns in planetary motions, and even though he could not see them immediately, he carefully recorded daily positions of the stars and planets, resulting in a vast dataset of observations. The basic human "remembering" ability was not enough anymore — the data had to be stored on an external medium. Tycho carefully guarded his measurements, hoping to discover as much as possible himself, but he was not the one to find the pattern of planetary motion. His assistant, Johannes Kepler got a hold of the data after Tycho's death. He studied the data and came up with three simple laws which described the movements of planets around the Sun. The laws were somewhat weird (the planets are claimed to sweep equal areas along an ellipse for no apparent reason), but they fit the data well.

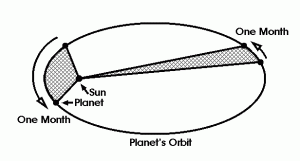
Kepler's Laws

This story perfectly mirrors basic human pattern discovery. There, a human first observes the world, then uses his brain to remember the observations, analyze them, find a simple regularity, and come up with an abstract summarizing symbol. Here the exact same procedure is performed on a larger scale: a human performs observations, a paper medium is used to store them, another human's mind is used to perform the analysis, the result is a set of summarizing laws.

Isaac Newton

Still a hundred years later, Isaac Newton looked hard at both Galileo's and Kepler's models and managed to summarize them further into a single equation: the law of gravity. It is somewhat weird (everything is claimed to be attracted to everything for no apparent reason), but it fits the data well. And the game is not over yet, three centuries later we are still looking hard to understand Gravity.

Where are we going

As we play the game, we gradually run out of the "obvious" patterns. Detecting new laws of nature and society becomes more and more complicated. Tycho Brahe had to delegate his "memory" capabilities to paper. In the 20th century, the advent of automation helped us to delegate not only "memory", but the observation process itself. Astronomers do not have to sit at their telescopes and manually write down stellar positions anymore — automated radar arrays keep a constant watch on the sky. Same is true of most other science disciplines to various extents. The last part of this puzzle which is not fully automated yet is the analysis part. Not for long...

Part II. Computers Discover the World

Manufactured life

Vacuum tube

The development of electricity was the main industrial highlight of the XIXth century. One particularly important invention of that century was an incredibly versatile electrical device called the vacuum tube. A lightbulb is a vacuum tube. A neon lamp is a vacuum tube. A CRT television set is a vacuum tube. But, all the fancy glowing stuff aside, the most important function of a vacuum tube turned out to be its ability to act as an electric current switcher. Essentially, it allowed to hardwire a very simple program:

if (wire1) then (output=wire2) else (output=wire3)

It turns out that by wiring thousands of such simple switches together, it is possible to implement arbitrary algorithms. Those algorithms can take input signals, perform nontrivial transformations of those signals, and produce appropriate outputs. But the ability to process inputs and produce nontrivial reactions is, in fact, the key factor distinguishing the living beings from lifeless matter. Hence, religious, spiritual, philosophical and biological aspects aside, the invention of electronic computing was the first step towards manufacturing life.

Of course, the first computers were not at all like our fellow living beings. They could not see or hear, nor walk or talk. They could only communicate via signals on electrical wires. They could not learn — there was no mechanisms to automaticaly rewire the switches in response to outside stimuli. Neither could they recognize and "remember" patterns in their inputs. In general, their hardwired algorithms seemed somewhat too simple and too predictable in comparison to living organisms.

Transistors

But development went on with an astonishing pace. The 1940's gave us the most important invention of the XXth century: the transistor. A transistor provides the same switching logic as a vacuum tube, but is tiny and power-efficient. Computers with millions and billions of transistors became gradually available. Memory technologies caught up: bytes grew into kilobytes, megabytes, gigabytes and terabytes (expect to see a cheap petabyte drive at your local computer store in less than 5 years). The advent of networking and the Internet, multicore and multiprocessor technologies followed closely. Nowadays the potential for creating complex, "nontrivial" lifelike behaviour is not limited so much by the hardware capabilities. The only problem left to solve is wiring the right program.

Reasoning

The desire to manufacture "intelligence" surfaced early on in the history of computing. A device that can be programmed to compute, must be programmable to "think" too. This was the driving slogan for computer science research in most of the 1950-1980s. The main idea was that "thinking", a capability defining human intellectual superiority over fellow mammals, was mainly related to logical reasoning.

"Socrates is a man. All men are mortal. => Hence, Socrates is mortal."

As soon as we teach computers to perform such logical inferences, they will become capable of "thinking". Many years of research have been put in to this area and it was not in vain. By now, computers are indeed quite successful at performing logical inference, playing games and searching for solutions of complex discrete problems. But the catch is, this "thinking" does not feel like being proper "intelligence". It is still just a dumb preprogrammed cause-and-effect thing.

The Turing Test

Alan Turing

A particular definition of "thinking" was provided by Alan Turing in his Turing test: let us define intelligence as a capability of imitating a human in a conversation, so that it would be indistinguishable from a real human. This is a hard goal to pursue. It obviously cannot be achieved by a bare logical inference engine. In order to imitate a human, computer has to know what a human knows, and that is a whole lot of knowledge. So, perhaps intelligence could be achieved by formalizing most of human knowledge within a powerful logical inference engine? This has been done, and done fairly well, but sadly, this still does not resemble real intelligence.

Reasoning by Analogy

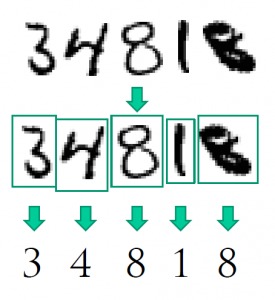
Optical character recognition

While hundreds of computer science researchers were struggling hard to create the ultimate knowledge-based logical system, real-life problems were waiting to be solved. No matter how good the computer became at solving abstract logical puzzles, he seemed helpless when faced with some of the most basic human tasks. Take, for example, character recognition. A single glimpse at a line of handwritten characters is enough for a human to recognize the letters (unless it is my handwriting, of course). But what logical inference should the computer do to perform it? Obviously, humans do not perform this task using reasoning, but rely on intuition instead. How can we "program" intuition?

The only practical way to automate character recognition turned out to be rather simple, if not to say dumb. Just store many examples of actual handwritten characters. Whenever you need to recognize a character, find the closest match in that database and voila! Of course, there are details which I sweep under the carpet, but the essence is here: recognition of characters can only be done by "training" on a dataset of actual handwritten characters. The key part of this "training" lies, in turn, in recognizing (or defining) the analogies among letters. Thus, the "large" task of recognizing characters is reduced to a somewhat "smaller" task of finding out which letters are similar, and what features make them similar. But this is pattern recognition, not unlike the rudimentary "remembering" ability of the early human ancestors.

The Meaning of Life

Please, observe and find the regularity in the following list:

• An ape observes its actions, recognizes regularities, and learns to purposefully grab things.
• Galileo observes falling bodies, recognizes regularities, and leans to predict the falling behaviour.
• Tycho Brahe observes stars, Johannes Keper recognizes regularities, and learns to predict planetary motion.
• Isaac Newton observes various models, recognizes regularities, and develops a general model of gravity.
• Computer observes handwritten characters, recognizes regularities, and learns to recognize characters.
• Computer observes your mailbox, recognizes regularities, and learns to filter spam.
• Computer observes natural language, recognizes regularities, and learns to translate.
• Computer observes biological data, recognizes regularities, and discovers novel biology.

Unexpectedly for us, we have stumbled upon a phenomemon, which, when implemented correctly, really "feels" like true intelligence. Hence, intelligence is not about logical inference nor extensive knowledge. It is all about the skill of recognizing regularities and patterns. Humans have evolved from preprogrammed cause-and-effect reflexes through simple "remembering" all the way towards fairly sophisticated pattern analysis. Computers now are following a similar path and are gradually joining us in The Game. There is still a long way to go, but we have a clear direction: The Intelligence, achieving which means basically "winning" The Game. If anything at all, this is the purpose of our existence - discovering all the regularities in the surrounding world for the sake of total domination of Nature. And we shall use the best intelligence we can craft to achieve it (unless we all die prematurely, of course, which would be sad, but someday some other species would appear to take a shot at the game).

Epilogue. Strong AI

There is a curious concept in the philosophical realms of computer science — "The Strong AI Hypothesis". It relates to the distinction between manufacturing "true consciousness" (so-called "strong AI") and creating "only a simulation of consciousness" (the "weak AI"). Although it is impossible to distinguish the two experimentally, there seems to be an emotional urge to make the distinction. This usually manifests in argumentation of the following kind: "System X is not true artificial intelligence, because it is a preprogrammed algorithm; Humans will never create true AI, because, unlike us, a preprogrammed algorithm will hever have free will; etc."

Despite the seemingly unscientific nature of the issue, there is a way to look at it rationally. It is probably true that we shall never admit "true intelligence" nor "consciousness" to anything which acts according to an algorithm which is, in some sense, predictable or understandable by us. On the other hand, every complex system that we ever create, has to be made according to clearly understandable blueprints. The proper way of phrasing the "Strong AI" question is therefore the following: is it possible to create a system, which is built according to "simple" blueprints, and yet the behaviour of which is beyond our comprehension.

Cellular automaton

The answer to this question is not immediately clear, but my personal opinion is that it is a strong "yes". There are at least three kinds of approaches known nowadays, which provide a means for us to create something "smarter" than us. Firstly, using everything fractal, cellular, and generally chaotic is a simple recipe for producing uncomprehensibly complex behaviour from trivial rules. The problem with this approach, however, is that there is no good methodology for crafting any useful functions into a chaotic system.

The second candidate is anything neural — obviously the choice of Mother Nature. Neural networks have the same property of being able to demonstrate behaviour, which is not immediately obvious from the neurons or the connections among them. We know how to train some types of networks and we have living examples to be inspired by. Nonetheless, it is still hard to actually "program" neural networks. Hence, the third and the most promising approach — general machine learning and pattern recognition.

The idea of a pattern recognition-based system is to use a simple algorithm, accompanied by a huge dataset. Note that the distinction between the "algorithm" and the "dataset" here draws a clear boundary between two parts of a single system. The "algorithm" is the part which we need to understand and include in our "blueprints". The "data" is the remaining part, which we do not care knowing about. In fact, the data can be so vast, that no human is capable of grasping it completely. Collecting petabytes is no big deal these days any more. This is a perfect recipe for making a system which will be capable of demonstrating behaviour that would be unpredictable and "intelligent" enough for us to call it "free will".

Think of it...

That is, if we are lucky and everything is done according to the proper tradition of doing statistics with 1% confidence intervals. In practice, things are probably even worse (many use 5% for instance), but this is what you would expect when everyone used proper methodology.

Think about it...

A cute joke by Margus from the recent EWSCS09 Crapcon session.

Symbols and Reality

Mathematics is a language. An abstract set of generic symbols for describing concepts, objects and systems. Take, for example, the symbol "5", "five". What is it? Is it a real-world object? No. It is just a symbol. You are free to attach to it any interpretation that you deem appropriate. Of course, most of the times you would use the common interpretation of "5" as a natural number, denoting, well, "five of something". Literally meaning that you can count something as "this, this, this, this and this".

Take a moment to reflect on the degree of generality of this simple concept, "five". It can be applied to practically anything. Five apples, five centimeters, five centuries are notions as different from each other as you could imagine, and yet all of them relate to the concept "five". On the other hand, it is not too generic to be useless: "five" is radically different from "six", "seven", and an infinity of other numbers. This kind of magical balance between generality and specificity is common to mathematics. This is what makes mathematics both widely applicable and yet still incredibly useful.

Besides just giving us symbols like 5 or 6, mathematics provides an endless variety of ways for expressing "rules", "operations", "statements", "derivations", "computations" and the like, such as 5+5=10, or , etc. Once again, all of these rules, operations and statements need not necessarily bear any relation with reality. After all, they all are just a cunning play with symbols. And yet, quite often they do describe reality incredibly well. I know that 512 apples and 512 apples will make 1024 apples together. How do I know it? Certainly not because I checked it on real apples! I just believe that the real-world operation of "adding apples" can be satisfactory modeled using the formal symbolic framework of natural numbers and the operation of addition on them. Why do I believe it? This is a tricky philosophical question that we shall leave aside for now. But remember that any application of mathematics to the real world is always based on a belief that the chosen model describes the world well.

The Nature of Uncertainty

There are often cases where we would like to use mathematics to model "uncertainty". Now remember that from the point of view of pure math there are no such things as inherent "certainty" and "uncertainty". Mathematics will always operate on symbols and use precise, uniquely reproducible transformation rules between these symbols. Yet there are often cases when we, in our interpretations of these symbols, would like refer to certain entities as "uncertain". The reasons can be various:

1. Sometimes, we would like to use a single generalized concept to summarize multiple objects.
   - What is the height of a human?
   There is no single clear answer and yet it is possible to provide one using an uncertainty model such as a probability distribution.
2. Sometimes, we want to reason about some single numeric value which, even if it were well-defined, we just could not compute exactly.
   - What is the AVERAGE height of a human?
   In theory, it is a number you could measure by lining up all the people in the world and computing their average, but it is certainly an infeasible project.
3. Sometimes, the notion we would like to reason about is inherently not well-defined.
   - What is MY height, after all?
   The answer depends on a number of factors such as time, measuring equipment, my precise posture, etc. Instead of taking all of these into consideration, we prefer to exploit an uncertainty model.
4. Sometimes we just need a single concept to encapsulate a state of knowledge more sophisticated than pure numeric equality. For example, to express the fact like "my height IS GREATER THAN 150cm" without using the "greater than" operation.

There are also other situations, which are difficult to classify, but in all cases the idea is the same — for one reason or another we "don't know" (or "don't specify") the exact single quantity we want to reason about, an yet we still "know something" about it. In fact, amusingly, the amount of information that we use to represent an "uncertain" quantity is often much greater than the amount of information we would need to represent a "certain" one. For example, there are much more probability distributions than there are real numbers. Therefore, picking one probability distribution to represent our knowledge of a number is, in principle, a more informative step than picking a single real number. And yet, we call the former case "uncertainty" and the latter one "certainty". Because that's how we choose to name and interpret things, that's how we believe these concepts relate to reality.

Models of Uncertainty

The adjective "uncertain" is something you could, in theory, apply generically to any type of data. In a computer scientist's terms, it makes perfect sense to talk about datatypes "uncertain int", "uncertain real", "uncertain boolean", "uncertain string", "uncertain graph", "uncertain map" and maybe even "uncertain uncertain real" and the like. Let's limit ourselves here to the consideration of uncertain numbers only, as these are the most commonly used and well-studied types of uncertainty. So how do you model (or, say, "implement") "uncertain real"? Here is a short list of the most popular options:

1. Approximate numbers.Although you might not consider it as a smart approach, this is probably the most common choice in practice — using a usual number to represent an uncertain one. In this case the uncertainty is purely interpretative: instead of stating you would, perhaps, write , denoting your state of ignorance. Quite often you would not even care to use the approximate equality sign, presuming it is clear from the context that you are not supposed to provide an ideally exact measurement: — What is your height? — It is 180cm. This works quite well in simple real-life situations, such as buying a kilogram of apples or discussing the horsepowers in a friend's motorbike, but is also applicable to some more technical cases, such as computing the distance to the nearest star.The advantage of such implied uncertainty is that you do not really need to deal with it. All of your familiar arithmetic operations come for free, together with their well established interpretations and the nice properties, theories and theorems. The disadvantage is that once your data is approximate, all of these theories and theorems become approximate too. So, although it could often be acceptable to claim , you would have problems explaining more complicated steps, such as " for a continuous f".But what to do if you need to perform such steps? Consider intervals instead!
2. Intervals.The second most popular method of representing an uncertain real number is to provide an interval where it falls into. It is ubiquitous in engineering disciplines. Most often an interval is expressed either as or by following the significant figures convention (e.g. writing 180.00 to denote 180±0.01). It is an improvement over the previous approach, because now you have a way to quantify the effect of function application on uncertainty. For example, a commonly used rule would be

   ,

   where f is a differentiable function.

3. Sets.An approach slightly more general than the "interval" technique would be to provide a set of values, to which the value of interest could belong to. So, instead of stating x = 5 you could write, for example, .This allows for more mathematical rigour. For example: . Moreover, besides the standard algebraic operations, the set representation allows to update the knowledge about an uncertain value easily using set unions and intersections:

   .

   However, sets are "heavy" object to work with, so you don't see this approach being used too often in practical computations. Some Monte-Carlo simulations would use a set to represent approximate solutions, but they would convert it to a probability distribution as soon as possible. This leads us to the next item on the list.

4. Probability distributions.If the previous methods were either too crude, too ad-hoc or too heavy, then probability theory was designed to provide flexible balance and help overcome most of their drawbacks. To represent a number it suggests us to use a probability measure - an additive function that assigns a weight to each set, which could contain the value of interest. The greater the weight of a set - the more probable it is that the value belongs to that set. By convention, the minimum possible weight of a set is 0, which we usually interpret as "the value almost certainly does not belong to that set", and the maximum weight is 1, with a corresponding interpretation "the value almost certainly belongs there". Representing a function defined on sets is complicated, so usually we use a simpler equivalent representation: a cumulative distribution function (CDF) or a probability density function (PDF). The plot of the latter is especially insightful and provides a nice visual cue about the nature of uncertainty being modeled.It is impossible to enumerate all the virtues of using a probability distribution as an uncertainty model. A probability distribution is a flexible structure, capable of accomodating most "common" kinds of uncertainty. There is an authoritative, well-developed theory and a wide range of both practical and theoretical tools available. Besides the standard algebraic operations, you have rules for updating knowledge (such as the Bayes rule) and a range of facilities for decision making (estimation, hypothesis testing, etc). Finally, there are various interpretations available for you to choose from.Of course, there are potential drawbacks, too. On the practical side, it is not always computationally convenient to work with a probability measure. It is a function, after all, and when specified arbitrarily it can either take too much space to represent or too much time to compute. The use of smoothing and approximation techniques can somewhat relieve the problem, but comes at the price of additional assumptions and simplifications. Secondly, a probability distribution is not capable of representing any kind of uncertainty: for example, there is no probability distribution corresponding to the statement "x < 5". Thirdly, the requirement for a probability density to be normalized to sum to 1 is sometimes inconvenient (because you have to normalize) or unintuitive (because it seems to declare that there is a single uncertain value "hidden inside").

   

   For example, consider the picture on the right and try to provide a concise description of the set of black pixels on it. This will be an uncertain notion because, well, a gray pixel is also somewhat black, isn't it? And although you could provide a probability distribution of "black" on the picture, you would probably intuitively prefer to assign a "truth-value" between 0 and 1 to each pixel, with 1 corresponding to "certainly black" and 0 to "certainly not black". This would, however, violate the "sum-to-one" normalization rule and thus would not be a probability density. What would it be? A fuzzy set.

5. Fuzzy sets.A fuzzy set is a set whose elements can have a degree of membership between 0 and 1. It is therefore something inbetween a set (because it "feels" like a set) and a probability density (because it is a function, only this time normalized to have a maximum of 1, instead of the integral of 1). A person familiar with probability theory will also easily recognize a straightforward analogy of a fuzzy set to a likelihood function.Fuzzy sets seem to be a natural uncertainty model in various circumstances, such as the "black pixels" example above. They are often conceptually simpler to specify than probability densities, and lack the interpretation controversy surrounding probability theory. On the other hand, the theory of fuzzy sets is not as extensive as that of probabilities. It is rich in operations like max and min, which makes some things computationally difficult. Besides, the lack of a universal interpretation for fuzzy membership values results in a lack of simple unique decision-making facilities. There are just way too many defuzzification rules to choose from.
6. ... and more.A variety of other approaches is available, the most important ones being Possibility theory, and Dempster-Shafer theory. However, as this text has already grown too long for a blog post, I shall leave the detailed description of these to Wikipedia.

Summary

The main message of this exposition is actually quite simple. There are various approaches to modeling uncertainty. They differ in the type of supported operations and, most importantly, in the way we interpret them and map to the real world entities. But nonetheless, these are all still just methods for modeling uncertainty, each with its own advantages and limitations. Moreover, in most situations, as long as you use the math "reasonably", the models are approximately equivalent in terms of the results and decisions you might end up with using them. That is probably the reason why practitioners would rarely consider anything more sophisticated than a probability measure (except, perhaps, when they are feeling adventurous). And that is why it can sometimes be complicated to promote the more "modern" approaches without the awkward looks from the side of the "traditional statistics". After all, these approaches are competing on the same field with The One and Only, Probability Theory.

Logic versus Statistics

Consider the two algorithms presented below.

Algorithm 1:

   If, for a given brick B,
      B.width(cm) * B.height(cm) * B.length(cm) > 1000
   Then the brick is heavy

Algorithm 2:

   If, for a given male person P,
      P.age(years) + P.weight(kg) * 4 - P.height(cm) * 2 > 100
   Then the person might have health problems

Note that the two algorithms are quite similar, at least from the point of view of the machine executing them: in both cases a decision is produced by performing some simple mathematical operations with a given object. The algorithms are also similar in their behaviour: both work well on average, but can make mistakes from time to time, when given an unusual person, or a rare hollow brick. However, there is one crucial difference between them from the point of view of a human: it is much easier to explain how the algorithm "works'' in the first case, than it is in the second one. And this is what in general distinguishes traditional "logical" algorithms from the machine learning-based approaches.

Of course, explanation is a subjective notion: something, which looks like a reasonable explanation to one person, might seem incomprehensible or insufficient to another one. In general, however, any proper explanation is always a logical reduction of a complex statement to a set of "axioms". An "axiom" here means any "obvious" fact that requires no further explanations. Depending on the subjective simplicity of the axioms and the obviousness of the logical steps, the explanation can be judged as being good or bad, easy or difficult, true or false.

Here is, for example, an explanation of Algorithm 1, that would hopefully satisfy most readers:

• The volume of a rectangular object can be computed as its width*height*length. (axiom, i.e. no further explanation needed)
• A brick is a rectangular object. (axiom)
• Thus, the volume of a brick can be computed as its width*height*length. (logical step)
• The mass of a brick is its volume times the density. (axiom)
• We consider the density of a brick to be at least 1g/cm³ and we consider a brick heavy if it weighs at least 1 kg. (axiom)
• Thus a brick is heavy if its mass > width*height*length > 1000. (logical step, end of explanation)

If you try to deduce a similar explanation for Algorithm 2 you will probably stumble into problems: there are no nice and easy "axioms" to start with, unless, at least, you are really deep into modeling body fat and can assign a meaning to the sum of a person's age with his weight. Things become even murkier if you consider a typical linear classification algorithm used in OCR systems for deciding whether a given picture contains the handwritten letter A or not. The algorithm in its most simple form might look as follows:

   If 
   Then there is a letter A on the picture,

where are some real numbers that were obtained using an obscure statistical procedure from an obscure dataset of pre-labeled pictures. There is really no good way to explain why the values of are what they are and how this algorithm gets the result, other than to present the dataset of pictures it was trained upon and state that "well, these are all pictures of the letter A, therefore our algorithm detects the letter A on pictures".

Note that, in a sense, such an "explanation" uses each picture of the letter A from the training set as an axiom. However, these axioms are not the kind of statements we used to justify Algorithm 1. The evidence they provide is way too weak for traditional logical inferences. Indeed, the fact that one known image has a letter A on it does not help much in proving that some other given image has an A too. Yet, as there are many of these "weak axioms", one statistical inference step can combine them into a well-performing algorithm. Notice how different this step is from the traditional logical steps, which typically derive each "strong" fact from a small number of other "strong" facts.

So to summarize again: there are two kinds of algorithms, logical and statistical.
The former ones are derived from a few strong facts and can be logically explained. Very often you can find the exact specifications of such algorithms in the internet. The latter ones are based on a large number of "weak facts" and rely on induction rather than logical (i.e. deductive) explanation. Their exact specification (e.g. the actual values for the parameters used in that OCR classifier) does not make as much general sense as the description of classical algorithms. Instead, you would typically find general principles for constructing such algorithms.

The Human Aspect

What I find interesting, is that the mentioned dichotomy stems more from human psychology than mathematics. After all, the "small" logical steps as well as the "big" statistical inference steps are all just "steps" from the point of view of maths and computation. The crucial difference is mainly due to a human aspect. The logical algorithms, as well as all of the logical decisions we make in our life, is what we often call "reason" or "intelligence". We make decisions based on reasoning many times a day, and we could easily explain the small logical steps behind each of them. But even more often do we make the kind of reason-free decisions that we call "intuitive". Take, for example, visual perception and body control. We do these things by analogy with our previous experiences and cannot really explain the exact algorithm. Professional intuition is another nice example. Suppose a skilled project manager says "I have doubts about this project because I've seen a lot of similar projects and all of them failed". Can he justify his claim? No, no matter how many examples of "similar projects" he presents, none of them will be considered as reasonable evidence from the logical point of view. Is his decision valid? Most probably yes.

Thus, the aforementioned classes of logical (deductive) and statistical (inductive) algorithms seem to directly correspond to reason and intuition in the human mind. But why do we, as humans, tend to consider intuition to be inexplicable and thus make "less sense" than reason? Note that the formal difference between the two classes of algorithms is that in the former case the number of axioms is small and the logical steps are "easy". We are therefore capable of representing the separate axioms and the small logical steps in our minds somehow. However, when the number of axioms is virtually unlimited and the statistical step for combining them is way more complicated, we seem to have no convenient way of tracking them consciously due to our limited brain capacity. This is somewhat analogous to how we can "really understand" why 1+1=2, but will have difficulties trying to grasp the meaning of 121*121=14641. Instead, the corresponding inductive computations can be "wired in" to the lower, unconscious level of our neural tissue by learning patterns from experience.

The Consequences

There was a time at the dawn of computer science, when much hope was put in the area of Artificial Intelligence. There, people attempted to devise "intelligent" algorithms based on formal logic and proofs. The promise was that in a number of years the methods of formal logic would develop to such heights, that would allow computer algorithms to attain "human" level of intelligence. That is, they would be able to walk like humans, talk like humans and do a lot of other cool things that we humans do. Half a century has passed and this still didn't happen. Computer science has seen enormous progress, but we have not found an algorithm based on formal logic that could imitate intuitive human actions. I believe that we never shall, because devising an algorithm based on formal logic actually means understanding and explaining an action in terms of a fixed number of axioms.

Firstly, it is unreasonable to expect that we can precisely explain much of the real world, because, strictly speaking, there exist mathematical statements that can't in principle be explained. Secondly, and most importantly, this expectation contradicts the assumption that most "truly human" actions are intuitive, i.e. we are simply incapable of understanding them.

Now what follows is a strange conclusion. There is no doubt that sooner or later computers will get really good at performing "truly human" actions, the trend is clear already. But, contradictory to our expectations, the fact that we shall create a machine that acts like a human will not really bring us closer to understanding how "a human" really "works". In other words, we shall never create Artificial Intelligence. What we are creating now, whether we want it or not, is Artificial Intuition.