Four Years Remaining

Can't help sharing this lovely example, illustrating the way Python interns small integers, the lower level use of the id function as well as the power of the ctypes module.

import ctypes
def deref(addr, type_):
    return ctypes.cast(addr, ctypes.POINTER(type_))

deref(id(29), ctypes.c_int)[4] = 100

> 29
100

> 29*100
10000

> 25+4
100

Note that depending on the version of Python the value of the integer may be stored at either offset [4] or [6].

I had to replace my SIM card today. The old one was mini-sized and I needed a micro-sized one. My previous SIM card stayed with me for about 20 years or so. I have gone through high school, university, and traveled around to countless places with it. I changed my phone several times, starting from an older, bulkier Nokia through several candy-bar Nokias and a couple of smartphones. My personal computer evolved from a 200MHz Pentium with 16MB RAM to a 2.8GHz quad-core with 32GB RAM. But my SIM card always stayed the same. Let me dedicate this post to the memory of this glorious tiny computer - the most long-lasting and reliable piece of computing equipment I have ever used.

My retiring SIM card. The mobile operator changed its name from Radiolinja to Elisa in 2000, but the SIM card did not care.

What is a SIM card?

Your SIM card is just another smart card, technologically similar to any of the "chip-and-pin" bank cards in your wallet, your ID card and even your contactless public transport tickets (which communicate using the same set of protocols, just wirelessly). Note, however, that banks started to switch from magnetic to "chip-and-pin" credit cards and countries began issuing smart-card-based identity documents only about 15 years ago or so. SIM cards, on the other hand, had been in wide use much earlier, long before the term "smart card" became a popularized buzzword.

All smart cards are built to serve one primary purpose - identification. The card stores a secret key (which is impossible to retrieve without disassembling the card using ultra-high-tech lab equipment), and provides a way to execute the following challenge-response protocol: you send a random string (a challenge) to the card. The card encrypts the string using the stored key and returns the response. The correctness of this response can now be verified by a second party (e.g. the mobile operator, the bank or a website using ID-card authentication). The actual details of the computation differ among the various smart cards. For example, some use symmetric while other - asymmetric cryptography. Some cards provide additional services, such as creating digital signatures or storing information on the card. None the less, identification is always the core function. This explains the name of the SIM card: Subscriber Identity Module. It is a module, which identifies you (the subscriber) to the network provider.

What is inside a SIM card?

The best way to understand what is inside a SIM (or any other type of smart-) card is to connect it to your computer and "talk" to it. Many laptops have integrated smart-card readers nowadays, so if you find a suitable frame for your nano/micro/mini-SIM, you may simply put it into the reader just as you would do with an ID or a bank card.

Old mini-SIM in a frame from a newer card

Note, though, that if your frame is flimsy and not fitting perfectly (as is mine on the photo above) you run the risk of losing the chip somewhere in the depths of the card reader slot before you even manage to slide it in completely. Hence, in my case, a tiny cross-style USB card reader was a more convenient and reliable option:

SIM in a frame in a reader

Plug it in, wait until the system recognizes the device, and we are ready to talk. There are many tools for "talking" to the card on a low level, but one of the best for the purposes of educational exploration is, in my opinion, the program called CardPeek. Let us fire it up. At start up it asks for the card reader to use (note that you can use it to explore both contact and contactless cards, if you have the necessary reader):

Select reader screen

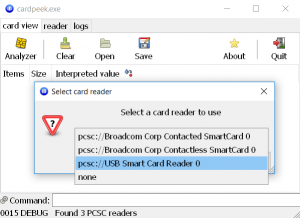
We can now click "Analyzer → GSM SIM", provide the PIN, wait a bit, and have the program extract a wealth of information stored on the card:

SIM card analyzed

Fun, right? Let us now see where all this data came from and what it actually means.

How does it work?

At the hardware level, a smart card has a very simple connector with six active pins, which are designed for sending and receiving data to and from the card:

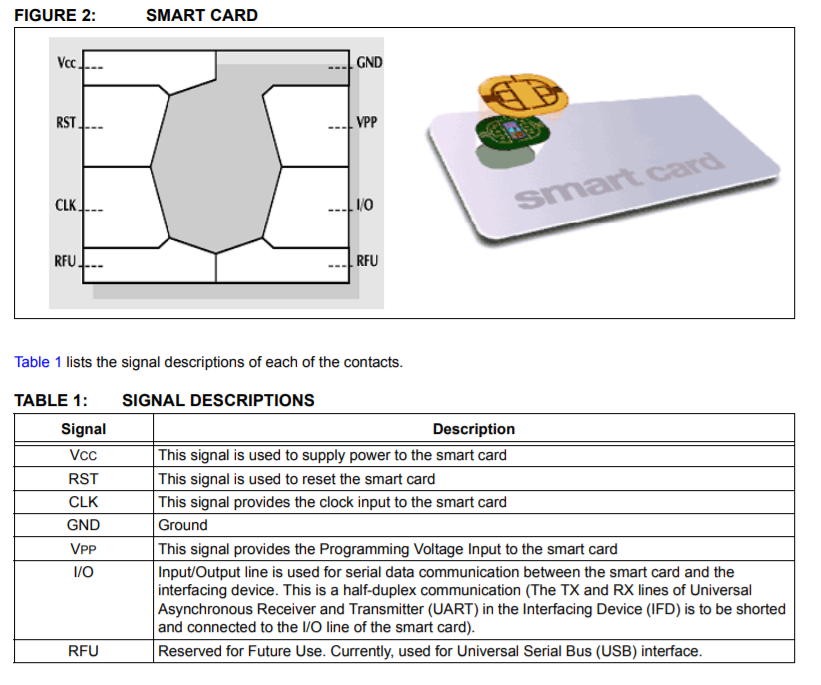
Smart card connectors (source)

Four pins (VCC, GND, CLK, I/O) are used for the basic half-duplex synchronous serial communication. RST is the reset pin, and VPP is used for supplying the higher voltage when (re)programming the card. When you first connect to the card, the protocol requires to zero the "reset" pin, to which the card will reply by sending a fixed sequence of bytes, identifying the card and its capabilities. It is known as the card's ATR ("Answer To Reset") string. You can see this string listed as the "cold ATR" entry in the screenshot named "SIM card analyzed" above.

Besides providing pre-packaged analysis scripts for various kinds of smart cards, CardPeek allows to send custom commands to the card by using its Lua scripting interface directly. This is what the "Command" text input at the bottom of the screen is for. Let us now switch to the "logs" tab and try sending some commands. First of all, we need to establish the connection to the card. This is done via the card.connect() call:

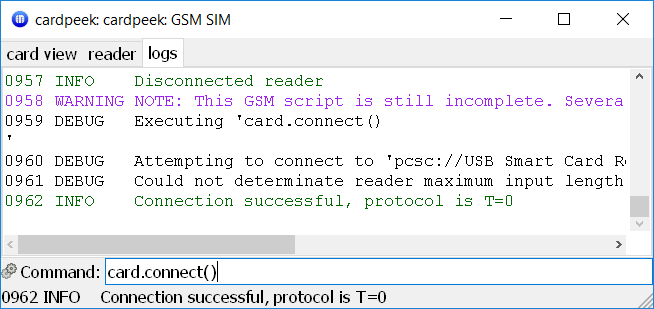
card.connect() example

The ATR string is received by the reader when the connection is first established. We can obtain it via card.last_atr() and print out to the log window in hex-encoded form using log.print and bytes:format (the documentation for all these APIs is available here):

ATR example

As we see, the ATR for my card happens to be 3BBA9400401447473352533731365320 (in hex).  If you search the web, you will find that this particular ATR is known to be  a signature of the Elisa SIM cards. It is not a random string, though, and every byte has a meaning. In particular:

• 3B is the "initial byte", and this particular value identifies the smart card as a SIM card.
• BA is the "format" byte. Its first four bits (1011) tell us that we have to expect fields TA1, TB1 and TD1 to follow. The last four bits denote the number 10 - the number of "historical bytes" at the end of the ATR.
• 94 is the field TA1, specifying the clock rate of the serial protocol
• 00 is the field TB1, specifying the programming voltage (apparently, the card is not re-programmable)
• 40 tells us that we have to read out another byte field TC2 (this is in the left-side part of the byte, 4 ) and that the card uses T=0 protocol (this is in the right-side part, 0).
• 14 is the promised TC2 field (not sure what it is meant for),
• the last 10 bytes are the "historical bytes", providing card manufacturer-specific information.

Greeting your Card

Now that we are connected, we can send various commands to the card. Let us proceed by example. The first command we might want to send is "VERIFY CHV", which is essentially greeting the card by providing our PIN1 code ("CHV" stands for "Card Holder Verification").

VERIFY CHV (source)

Every smart card command starts with a two-byte identifier (for example, A0 20 is the (hex) identifier of the VERIFY CHV command). It is followed by two parameter bytes P1 and P2. For example, the parameter P1 for VERIFY CHV is always 0, and P2 must indicate the number of the PIN we are submitting (i.e. 1 for PIN1, 2 for PIN2). Next comes P3 - a byte, specifying the length of the data which follows. For VERIFY CHV the data is the provided PIN itself, and it is always 8 bytes long. If the PIN is shorter than 8 bytes, it must be padded by bytes FF. The PIN itself is encoded in plain ASCII (i.e. 1234 would be 31 32 33 34).

Now, supposing my PIN1 is, in fact "1234", I can authenticate myself to the card via CardPeek as follows:

sw, resp = card.send(bytes.new(8, "A0 20 00 01 08 31 32 33 34 FF FF FF FF"))

Here, card.send is the sending command and bytes.new(8, ...) constructs an array of 8-bit bytes from a hex string (see CardPeek reference).

The sw and resp are the two components of the T=0 protocol response. For VERIFY CHV we only care that sw is equal to 9000, which means "OK". Note how this is printed in the log.

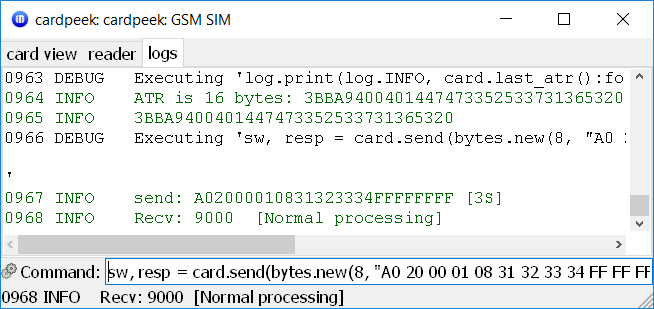
VERIFY CHV example

Beware that if you do not receive a 9000 response, it means that the card denied your PIN for some reason. Trying to submit a wrong PIN three times in a row will block the card.

Reading the Data

Now that we have identified ourselves to the card, let us try to read the data stored on it. The data on the card is organized in a hierarchy of files. It is this exact hierarchy that you can observe as the output of the "Analyzer" script. The root file is called "MF", it has the ICCID, TELECOM and GSM sub-files, which, in turn, have a number of predefined sub-files themselves, etc. The names are just conventions, the card itself uses two-byte identifiers for each file. For example, "MF" is actually 3F 00, "TELECOM" is 7F 10, etc. While the card is connected you can navigate around the file structure just like you would do in a normal operating system using the cd command, except that in smart-card lingo the corresponding command is called SELECT.

The binary form of the SELECT command is A0 A4 00 00 02 {x} {y}, where {x} {y} is the file identifier. Just like before, A0 A4 is the command code, 00 00 are the ignored P1 and P2 parameters, and 02 tells us that exactly two bytes must follow.

Consequently, if we wanted to select the file "MF (3f 00)/TELECOM (7F 10)/ADN (6F 3A)", which contains the address book records, we could achieve it by sending the following sequence of commands via CardPeek:

card.send(bytes.new(8, "A0 A4 00 00 02 3F 00"))
card.send(bytes.new(8, "A0 A4 00 00 02 7F 10"))
card.send(bytes.new(8, "A0 A4 00 00 02 6F 3A"))

Selecting files is a common task, and CardPeek provides a convenient shorthand: card.select("#7f10"). For some cards (not mine, unfortunately) it should also be possible to do things like card.select("/7f10/6f3a").

Once we have selected the ADN ("Abbreviated Dialing Numbers") file, we may read out the individual phone numbers from it using the READ RECORD command. The procedure is complicated by the fact that READ RECORD needs to be provided the "record size" as one of its parameters, which, in turn, must be taken from the response data of the last SELECT command, and this must be obtained via the GET RESPONSE command. The complete example would therefore be:

-- Select /TELECOM/ADN
card.select("#7F10")
sw, resp = card.select("#6F3A")

-- Read file metadata
GET_RESPONSE = "A0 C0 00 00"
sw, resp = card.send(bytes.new(8, GET_RESPONSE, bit.AND(sw, 0xff)))

-- Read out first record in the file
sw, resp = card.read_record('.', 1, resp:get(14))

-- Print the record to the log
log.print(log.INFO, resp:format("%P"))

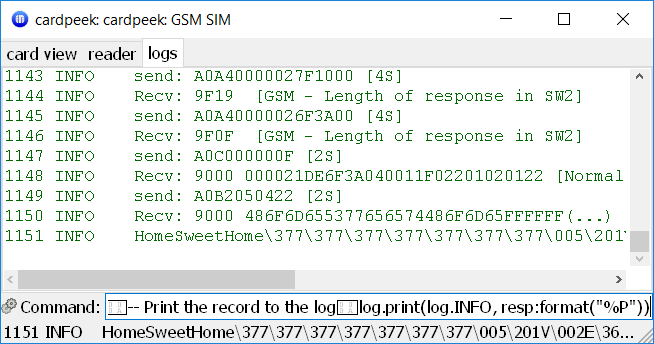
Reading out a phone record

Note that instead of printing the output to the log via log.print you could also show a message box:

ui.readline(resp:format("%P"))

or append a new node to the tree in the "card view" tab:

nodes.append(nodes.root(), {classname="block", 
                            label="Name", 
                            val=resp:format("%P"), 
                            size=#resp})

In fact, at this point you should go and read the script $HOME/.cardpeek/scripts/gsm (beta).lua. It contains the code we ran in the beginning of this post to analyze the card. The script simply sends the relevant commands to the card and appends all responses as nodes to the tree.

Authentication

While data storage is a useful capability of a SIM card, its main purpose is subscriber authentication. Thus, our acquaintance with the SIM card would be incomplete without checking the corresponding function out as well. It is quite simple:

RUN GSM ALGORITHM (source)

That is, the process is the following: we send the byte sequence A0 88 00 00 10, followed by a 16 byte-long challenge string (which is normally given by the mobile operator when the phone joins the network). The SIM card responds with 12 bytes, of which the first 4 we should send back to the mobile operator for verification, and use the remaining 8 as a cipher key.

Before we can use the RUN GSM ALGORITHM command we need to verify our PIN1 (already done) and SELECT the GSM (7F 20) file:

RUN_GSM_ALGO = "A0 88 00 00 10"
GET_RESPONSE = "A0 C0 00 00"
DF_GSM = "#7F20"

CHALLENGE_STRING = "00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00"

-- Select GSM file
card.select(DF_GSM)

-- Send the challenge data
sw, resp = card.send(bytes.new(8, RUN_GSM_ALGO, CHALLENGE_STRING))

-- Read 12-byte-long response
sw, RESPONSE_STRING = card.send(bytes.new(8, GET_RESPONSE, 12))
log.print(log.INFO, RESPONSE_STRING:format("%D"))

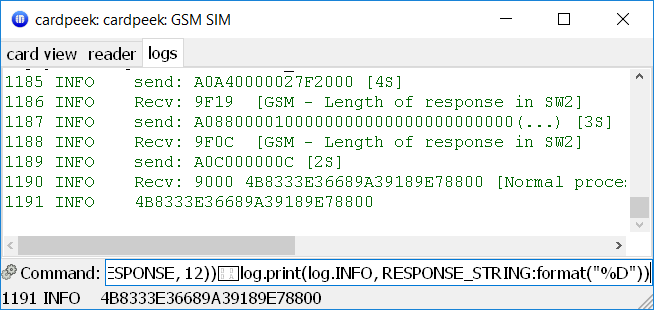
RUN GSM ALGORITHM example

And that is it. I hope you learned to understand and appreciate your SIM card a bit more today.

Every student of computer science, who has managed to keep even a tiny shred of attention at their algorithms course, should know that sorting numbers is a task that requires at least time in general. There are some special cases, such as sorting small integers, where you can use counting sort or radix sort to beat this baseline, but as long as your numbers are hypothetically arbitrarily large, you are stuck with the lower bound. Right?

Well, not really. One thing that many algorithms courses tend to skim over rather briefly is the discussion of the choice of the computation model, under which the algorithm of interest is supposed to run. In particular, the bound for sorting holds for the comparison-only model of computation — the abstract situation where the algorithm may only perform pairwise comparisons of the numbers to be sorted. No arithmetic, bit-shifts or anything else your typical processor is normally trained to do is allowed. This is, obviously, not a very realistic model for a modern computer.

Let us thus consider a different computation model instead, which allows our computer to perform any of the basic arithmetic or bitwise operations on numbers in constant time. In addition, to be especially abstract, let us also assume that our computer is capable of handling numbers of arbitrary size. This is the so-called unit-cost RAM model.

It turns out that in this case one can sort arbitrarily large numbers in linear time. The method for achieving this (presented in the work of W. Paul and J. Simon, not to be confused with Paul Simon) is completely impractical, yet quite insightful and amusing (in the geeky sense). Let me illustrate it here.

Paul-and-Simon Sorting

The easiest way to show an algorithm is to step it through an example. Let us therefore consider the example task of sorting the following array of three numbers:

a = [5, 3, 9]

Representing the same numbers in binary:

[101, 11, 1001]

Our algorithm starts with a linear pass to find the bit-width of the largest number in the array. In our case the largest number is 9 and has 4 bits:

bits = max([ceil(log2(x)) for x in a])     # bits = 4
n = len(a)                                 # n = 3

Next the algorithm will create a -bit number A of the following binary form:

 1 {5} 1 {5} 1 {5} 1 {3} 1 {3} 1 {3} 1 {9} 1 {9} 1 {9}

where {9}, {3} and {5} denote the 4-bit representations of the corresponding numbers. In simple terms, we need to pack each array element repeated times together into a single number. It can be computed in linear time using, for example, the following code:

temp, A = 0, 0
for x in a:
    temp = (temp<<(n*(bits+1))) + (1<<bits) + x
for i in range(n):
    A = (A<<(bits+1)) + temp

The result is 23834505373497, namely:

101011010110101100111001110011110011100111001

Next, we need to compute another 45-bit number B, which will also pack all the elements of the array times, however this time they will be separated by 0-bits and interleaved as follows:

 0 {5} 0 {3} 0 {9} 0 {5} 0 {3} 0 {9} 0 {5} 0 {3} 0 {9}

This again can be done in linear time:

temp, B = 0, 0
for x in a:
    temp = (temp<<(bits+1)) + x
for i in range(n):
    B = (B<<(n*(bits+1))) + temp

The result is 5610472248425, namely:

001010001101001001010001101001001010001101001

Finally, here comes the magic trick: we subtract B from A. Observe how with this single operation we now actually perform all pairwise subtractions of the numbers in the array:

A = 1 {5} 1 {5} 1 {5} 1 {3} 1 {3} 1 {3} 1 {9} 1 {9} 1 {9} 
B = 0 {5} 0 {3} 0 {9} 0 {5} 0 {3} 0 {9} 0 {5} 0 {3} 0 {9}

Consider what happens to the bits separating all the pairs. If the number on top is greater or equal to the number on the bottom of the pair, the corresponding separating bit on the left will not be carried in the subtraction, and the corresponding bit of the result will be 1. However, whenever the number on the top is less than the number on the bottom, the resulting bit will be zeroed out due to carrying:

A   = 1 {5} 1 {5} 1 { 5} 1 { 3} 1 {3} 1 { 3} 1 {9} 1 {9} 1 {9} 
B   = 0 {5} 0 {3} 0 { 9} 0 { 5} 0 {3} 0 { 9} 0 {5} 0 {3} 0 {9}
A-B = 1 {0} 1 {2} 0 {12} 0 {14} 1 {0} 0 {10} 1 {4} 1 {6} 1 {0}

The same in binary (highlighted groups correspond to repetitions of the original array elements in the number A):

A   = 1 0101 1 0101 1 0101|1 0011 1 0011 1 0011|1 1001 1 1001 1 1001
B   = 0 0101 0 0011 0 1001|0 0101 0 0011 0 1001|0 0101 0 0011 0 1001
A-B = 1 0000 1 0010 0 1100|0 1110 1 0000 0 1010|1 0100 1 0110 1 0000

Each "separator" bit of A-B is effectively the result of a comparison of every array element with every other. Let us now extract these bits using a bitwise AND and sum them within each group. It takes another couple of linear passes:

x = A-B >> bits
mask, result = 0, 0
for i in range(n):
    mask = (mask<<(n*(bits+1))) + 1
for i in range(n):
    result += x & mask
    x = x >> (bits+1)

The result is now the following number:

result = 10|000000000000001|000000000000011

It is a packed binary representation of the array r = [2, 1, 3]. The number 2 here tells us that there are two elements in a, which are less or equal than a[0]=5. Similarly, the number 1 says that there is only one element less or equal than a[1]=3, and the number 3 means there are three elements less or equal than a[2]=9. In other words, this is an array of ranks, which tells us how the original array elements should be rearranged into sorted order:

r = [result >> (n*(bits+1)*(n-i-1)) & ((1<<(n*(bits+1)))-1) 
                                          for i in range(n)]
a_sorted = [None]*n
for i in range(n):
    a_sorted[r[i]-1] = a[i]

And voilà, the sorted array! As presented above, the method would only work for arrays consisting of distinct non-negative integers. However, with some modifications it can be adapted to arbitrary arrays of integers or floats. This is left as an exercise to the reader.

The General Implications

There are several things one can learn from the "Paul-and-Simon sort". Firstly, it shows the immense power of the unit-cost RAM computational model. By packing arbitrary amounts of data into a single register of unlimited size, we may force our imaginary computer to perform enormously complex parallel computations in a single step. Indeed, it is known that PSPACE-complete problems can be solved in polynomial time in the unlimited-precision RAM model. This, however, assumes that the machine can do arbitrary arithmetic operations. If you limit it to only additions, subtractions and multiplications (but not divisions or bit-shifts), you still cannot sort integers faster than even using infinitely-sized registers (this is the main result of the Paul and Simon's article that inspired this post). Not obvious, is it?

Of course, real computers can usually only perform constant-time operations on registers of a fixed size. This is formalized in the -bit word-RAM model, and in this model the "Paul and Simon sort" degrades from a into a algorithm (with memory consumption). This is a nice illustration of how the same algorithm can have different complexity based on the chosen execution model.

The third thing that the "Paul and Simon sort" highlights very clearly is the power of arithmetic operations on packed values and bitstrings. In fact, this idea has been applied to derive practically usable integer sorting algorithms with nearly-linear complexity. The latter paper by Han & Thorup expresses the idea quite well:

In case you need the full code of the step-by-step explanation presented above, here it is.

The Dark Side of the Bitcoin

Recall that Bitcoin is a currency, i.e. it is a technology, which aims to provide a store of value along with a payment medium. With all due respect to its steadily growing adoption, it would be fair to note that it is not very good at fulfilling either of these two functions currently. Firstly, it is not a very reliable store of value due to extreme volatility in the price. Secondly, and most importantly, it is a mediocre payment medium because it is slow and expensive.

A typical transfer costs around $2 nowadays and takes about an hour for a full confirmation (or longer, if you pay a smaller fee). When you need to transfer a million dollars, this looks like a reasonable deal. When you buy a chocolate bar at a grocery store (something one probably does more often than transferring a million), it is unacceptable. Any plain old bank's payment card would offer a faster and cheaper solution, which is ironic, given that Bitcoin was meant to be all friendly, distributed and free (as in freedom) while banks are, as we all know, evil empires hungry for our money, flesh and souls.

The irony does not end here. The evil banks typically provide some useful services in exchange for the fees they collect, such as an online self-service portal, 24h support personnel, cash handling and ATMs, some security guarantees, interests on deposits, etc. The friendly Bitcoin offers nothing of this kind. What is Bitcoin wasting our money on then? Electricity, mainly! The Proof of Work (PoW) algorithm employed in the Bitcoin's blockchain requires the computation of quintillions of random, meaningless hashes to "confirm" payments. The "miner" nodes, running the Bitcoin's network are collectively performing more than 5 000 000 000 000 000 000 (five quintillion or five exa-) hash computations every second, continuously consuming as much electricity as the whole country of Turkmenistan. The situation is even worse if you consider that Bitcoin is just one of many other "coins" built upon the PoW algorithm (Ethereum and Litecoin being the two other prominent examples), and their overall power consumption is only growing with each day.

Just think of it: most of the $2 fee a Bitcoin user needs to pay for a transaction will neither end up as someone's wage nor make a return on investment in someone's pocket. Instead, it will burn up in fossil fuels which generate power for the "miners", wasting precious resources of our planet, contributing to global warming and pushing poor polar bears faster towards extinction. Is all this mayhem at least a "necessary evil"? Sadly, it is not.

The Unnecessary Evil

Formally speaking, Proof of Work is an algorithm for achieving consensus among a distributed set of nodes which collectively maintain a common blockchain. Is it the only such algorithm? Of course not! Many alternative methods exist, most of them (if not all) are both faster and less energy-hungry. In fact, the only valuable property of PoW is its ingenious simplicity. In terms of implementation it may very well be among the simplest distributed blockchain consensus algorithms ever to be invented.

It is natural that a successful pioneering technology (such as the Bitcoin) is originally built from simple blocks. Progress comes in small steps and you cannot innovate on all fronts at once, after all. There must come a time, however, when the limitations of the initially chosen basic blocks become apparent and the technology gets upgraded to something more efficient. With more than $1 billion dollars in electricity bills paid by Bitcoin users last year for the inefficiency of PoW, Bitcoin has long surpassed this turning point, in my opinion.

Unfortunately, due to its pioneering status, enormous inertia, ongoing hype and the high stakes involved, Bitcoin continues to roll on its old wooden proof-of-work wheels with no improvement in sight, somewhy still being perceived as the leader in the brave new world of cryptocurrencies.

Are nearly-instant and nearly-free payment along with energy efficiency too much to ask from a real "currency of the future"? I do not think so. In fact, Bitcoin could be such a currency, if only it could switch from the evil Proof of Work to a different, fast and eco-friendly consensus algorithm.

Which algorithm could it be? Let me offer you an overview of some of the current options I am personally aware of, so you could decide for yourself.

The Eco-Friendly Blockchain Consensus

Consider a network of many nodes, which needs to maintain a common state for a chain of blocks. There seem to be roughly three general categories of algorithms which the nodes could employ for their purpose: Proof of Authority (PoA), Nakamoto Consensus, and Byzantine Fault Tolerance (BFT). Let us consider them in order.

Proof of Authority

Perhaps the most straightforward solution would be to nominate a fixed subset of nodes as "authoritative", and let any of them append new blocks by signing them cryptographically. To avoid conflicting updates, nodes may agree on a predefined round-robin signing order, honestly randomize their waiting intervals, or use some kind of a deterministic lottery for selecting the signer for next block, etc.

As this approach relies on a fixed subset of (reasonably) trusted nodes, it does not look robust and secure enough for a proper worldwide distributed blockchain. For example, in the limit case of a single trusted party it is equivalent to using a single service provider such as a bank. None the less, it is a convenient baseline and an important primitive, actually applicable to a wide range of real-life blockchain deployments. By relying on a set of well-behaving parties, a PoA blockchain actually sidesteps most of the complexities of a real distributed algorithm, and can thus be made to perform much faster than any of the "truly distributed" algorithms.

The Ethereum software provides an implementation of this approach for those who want to run private chains. PeerCoin relies on the PoA principle by having "checkpoint blocks" signed regularly by a trusted authority. Finally, the Delegated Proof of Stake algorithm makes PoA work on a larger scale by relying on voting. It is probably one of the most interesting practical implementations of the idea.

Delegated Proof of Stake

Delegated Proof of Stake (DPoS) is a consensus algorithm implemented in Graphene-based blockchains (BitShares, Steem, EOS). It is a variant of Proof of Authority, where the small set of authoritative delegate nodes is elected by voting. When electing the delegates, each node can cast the number of votes, proportional to their account value (or "stakeholder share"), thus "delegating their stake in the network". The elected authorities then participate in a simple and fast round-robin block confirmation with each node given a two second window for confirming the next block.

The security of DPoS hinges on the assumption that the nodes with the most stake in the system should generally manage to elect a set of reasonable authorities, and in case of errors, the misbehaving authorities will not cause too much trouble and will be quickly voted out. At the same time, being internally a PoA implementation, the DPoS-based blockchains are by an order of magnitude faster in terms of transaction throughput than any other currently running public blockchains. Notably, they can also naturally support fee-less transactions.

Nakamoto Consensus

Consider the variation of PoA, where there are no pre-selected trusted nodes (i.e. all nodes may participate in the algorithm). Each time a new block needs to be added to the chain, let us pick the node who will gain the right to add it according to some deterministic "lottery" system. The consensus can then be achieved by simply verifying that the resulting blockchain is conforming to the lottery rules at all times, and the conflicting chains are resolved by always preferring the "harder" chain (according to some notion of "hardness").

For example, the infamous Proof-of-Work is an example of such a method. The "lottery" here is based on the ability of a node to find a suitable nonce value. The "hardness" is simply the length of the chain. Such "lottery" methods are sometimes referred to as "Nakamoto consensus algorithms". In terms of efficiency, Nakamoto consensus algorithms are among the slowest consensus algorithms.

Several alternatives to the "PoW lottery" have been proposed. Let us review some of them.

Proof of Stake

Proof of Stake (PoS), first implemented in the Nxt cryptocurrency, is a Nakamoto consensus technique, where the nodes with a greater balance on their account are given a higher chance to "win the lottery" and sign the next block. The actual technique used in Nxt is the following: before signing a block every node obtains a pseudo-random "lottery ticket number" by hashing the last block data with its own identifier. If this number is smaller than

(where is a block-specific constant), the node gets the right to sign the next block. The higher the node's balance, the higher is the probability it will get a chance to sign. The rationale is that nodes with larger balances have more at stake, are more motivated to behave honestly, and thus need to be given more opportunities to participate in generating the blockchain.

Proof of Stake is typically considered as the primary alternative to Proof of Work without all the wasteful computation, and it should, in principle, be possible to transition the whole blockchain from the latter to the former. In fact, this is what may probably happen to Ethereum eventually.

Proof of Space

In Proof of Space (PoSpace), a consensus mechanism implemented in Burstcoin, the "miners" must first pre-generate a set of "lottery ticket numbers" in a particular manner for themselves, save these numbers on a hard drive and commit the hash (the Merkle tree root) of this complete ticket set to the blockchain. Then, similarly to Proof of Stake, by hashing the last block's data, a miner deterministically picks one of his own "lottery tickets" for the next block. If the value of this ticket, discounted by the number of tickets in possession, is small enough, the miner gets the right to sign the block. The more tickets a miner generates and stores, the better are his chances. When signing the block, the miner must present a couple of special hashes which he can only know if he constantly stores his complete set of tickets (or fully recomputes a large part of it every time, which is impractical). Consequently, instead of spending energy on the "mining" process, the nodes must constantly dedicate a certain amount of disk space to the algorithm.

Although it is probably among the less widely known methods, from both technical and practical standpoint, it is one of the most interesting techniques, in my opinion. Note how it combines the properties of PoS (speed and energy efficiency) with those of PoW (ownership of a real-world resource as a proxy for decentralization).

Proof of Burn

The idea behind Proof of Burn is to allow the nodes to generate their "lottery ticket numbers" by irretrievably transferring some coins to a nonexistent address and taking the hash of the resulting transaction. The resulting hash, scaled by the amount of coins burned, can then be used to gain the right to sign blocks just like in other Nakamoto lottery systems. The act of wasting coins is meant to be a virtual analogue of spending electricity on PoW mining, without actually spending it. Blockchains based purely on Proof of Burn do not seem to exist at the moment. However, the technique can  be used alongside PoW, PoS or other approaches.

Proof of Elapsed Time

Presumably, some Intel processors have specialized instructions for emitting signed tokens, which prove that a given process called a particular function a certain period of time ago. The Hyperledger project proposes to build a consensus algorithm around those. Each "miner" will gain the right to sign a block after it waits for a certain period of time. The token which proves that the miner did in fact wait the allotted time, would act as a winning lottery ticket. I do not see how this method could work outside of the trusted Intel-only environment or how is it better than a trivialized Proof of Stake (not sure I even understood the idea correcty), but I could not help mentioning it here for completeness' sake.

Hybrid Nakamoto Consensus Systems

Some systems interleave PoW and PoS confirmations, or add PoA signatures from time to time to lock the chain or speed-up block confirmations. In fact, it is not too hard to invent nearly arbitrary combinations of delegation, voting, payments, authorities and lotteries.

Byzantine Fault Tolerance

The Practical Byzantine Fault Tolerance (PBFT) algorithm offers an alternative solution to the consensus problem. Here the blockchain state is tracked by a set of "bookkeeping" nodes, which constantly broadcast all changes among themselves and consider a change reliably replicated when it is signed and confirmed by given quorum (e.g. 2/3) of the bookkeepers. The algorithms of this type can be shown to be reliable if no more than a third of the nodes are dishonest. The Ripple, Stellar and Antshares are examples of blockchains based on such techniques. This algorithm allows much higher transaction throughputs than Nakamoto consensus (PoW, PoS, PoSpace), yet it still lags behind the speed of PoA or DPoS.

The following is an expanded version of an explanatory comment I posted here.

Alice's Diary

Alice decided to keep a diary. For that she bought a notebook, and started filling it with lines like:

Alice did her best to keep a meticulous account of events, and whenever she had a discussion with friends about something that happened earlier, she would quickly resolve all arguments by taking out the notebook and demonstrating her records. One day she had a dispute with Bob about whether she lent him $250 earlier or not. Unfortunately, Alice did not have her notebook at hand at the time of the dispute, but she promised to bring it tomorrow to prove Bob owed her money.

Bob really did not want to return the money, so that night he got into Alice's house, found the notebook, found line 132 and carefully replaced it with "132. Kissed Dave". The next day, when Alice opened the notebook, she did not find any records about money being given to Bob, and had to apologize for making a mistake.

Alice's Blockchain

A year later Bob's conscience got to him and he confessed his crime to Alice. Alice forgave him, but decided to improve the way she kept the diary, to avoid the risk of forging records in the future. Here's what she came up with. The operating system Linups that she was using had a program named md5sum, which could convert any text to its hash - a strange sequence of 32 characters. Alice did not really understand what the program did with the text, it just seemed to produce a sufficiently random sequence. For example, if you entered "hello" into the program, it would output "b1946ac92492d2347c6235b4d2611184", and if you entered "hello " with a space at the end, the output would be "1a77a8341bddc4b45418f9c30e7102b4".

Alice scratched her head a bit and invented the following way of making record forging more complicated to people like Bob in the future: after each record she would insert the hash, obtained by feeding the md5sum program with the text of the record and the previous hash. The new diary now looked as follows:

Now each record was "confirmed" by a hash. If someone wanted to change the line 132 to something else, they would have to change the corresponding hash (it would not be 1010 anymore). This, in turn, would affect the hash of line 133 (which would not be 8204 anymore), and so on all the way until the end of the diary. In order to change one record Bob would have to rewrite confirmation hashes for all the following diary records, which is fairly time-consuming. This way, hashes "chain" all records together, and what was before a simple journal became now a chain of records or "blocks" - a blockchain.

Proof-of-Work Blockchain

Time passed, Alice opened a bank. She still kept her diary, which now included serious banking records like "Gave out a loan" or "Accepted a deposit". Every record was accompanied with a hash to make forging harder. Everything was fine, until one day a guy named Carl took a loan of $1000000. The next night a team of twelve elite Chinese diary hackers (hired by Carl, of course) got into Alice's room, found the journal and substituted in it the line "143313. Gave out a $1000000 loan to Carl" with a new version: "143313. Gave out a $10 loan to Carl". They then quickly recomputed all the necessary hashes for the following records. For a dozen of hackers armed with calculators this did not take too long.

Fortunately, Alice saw one of the hackers retreating and understood what happened. She needed a more secure system. Her new idea was the following: let us append a number (called "nonce") in brackets to each record, and choose this number so that the confirmation hash for the record would always start with two zeroes. Because hashes are rather unpredictable, the only way to do it is to simply try out different nonce values until one of them results in a proper hash:

To confirm each record one now needs to try, on average, about 50 different hashing operations for different nonce values, which makes it 50 times harder to add new records or forge them than previously. Hopefully even a team of hackers wouldn't manage in time. Because each confirmation now requires hard (and somewhat senseless) work, the resulting method is called a proof-of-work system.

Distributed Blockchain

Tired of having to search for matching nonces for every record, Alice hired five assistants to help her maintain the journal. Whenever a new record needed to be confirmed, the assistants would start to seek for a suitable nonce in parallel, until one of them completed the job. To motivate the assistants to work faster she allowed them to append the name of the person who found a valid nonce, and promised to give promotions to those who confirmed more records within a year. The journal now looked as follows:

A week before Christmas, two assistants came to Alice seeking for a Christmas bonus. Assistant Jack, showed a diary where he confirmed 140 records and Mary confirmed 130, while Mary showed a diary where she, reportedly, confirmed more records than Jack. Each of them was showing Alice a journal with all the valid hashes, but different entries! It turns out that ever since having found out about the promotion the two assistants were working hard to keep their own journals, such that all nonces would have their names. Since they had to maintain the journals individually they had to do all the work confirming records alone rather than splitting it among other assistants. This of course made them so busy that they eventually had to miss some important entries about Alice's bank loans.

Consequently, Jacks and Mary's "own journals" ended up being shorter than the "real journal", which was, luckily, correctly maintained by the three other assistants. Alice was disappointed, and, of course, did not give neither Jack nor Mary a promotion. "I will only give promotions to assistants who confirm the most records in the valid journal", she said. And the valid journal is the one with the most entries, of course, because the most work has been put into it!

After this rule has been established, the assistants had no more motivation to cheat by working on their own journal alone - a collective honest effort always produced a longer journal in the end. This rule allowed assistants to work from home and completely without supervision. Alice only needed to check that the journal had the correct hashes in the end when distributing promotions. This way, Alice's blockchain became a distributed blockchain.

Bitcoin

Jack happened to be much more effective finding nonces than Mary and eventually became a Senior Assistant to Alice. He did not need any more promotions. "Could you transfer some of the promotion credits you got from confirming records to me?", Mary asked him one day. "I will pay you $100 for each!". "Wow", Jack thought, "apparently all the confirmations I did still have some value for me now!". They spoke with Alice and invented the following way to make "record confirmation achievements" transferable between parties.

Whenever an assistant found a matching nonce, they would not simply write their own name to indicate who did it. Instead, they would write their public key. The agreement with Alice was that the corresponding confirmation bonus would belong to whoever owned the matching private key:

To transfer confirmation bonuses between parties a special type of record would be added to the same diary. The record would state which confirmation bonus had to be transferred to which new public key owner, and would be signed using the private key of the original confirmation owner to prove it was really his decision:

In this example, record 284 transfers bonus for confirming record 132 from whoever it belonged to before (the owner of private key 6669, presumably Jack in our example) to a new party - the owner of private key 1111 (who could be Mary, for example). As it is still a record, there is also a usual bonus for having confirmed it, which went to owner of private key 4442 (who could be John, Carl, Jack, Mary or whoever else - it does not matter here). In effect, record 284 currently describes two different bonuses - one due to transfer, and another for confirmation. These, if necessary, can be further transferred to different parties later using the same procedure.

Once this system was implemented, it turned out that Alice's assistants and all their friends started actively using the "confirmation bonuses" as a kind of an internal currency, transferring them between each other's public keys, even exchanging for goods and actual money. Note that to buy a "confirmation bonus" one does not need to be Alice's assistant nor register anywhere. One just needs to provide a public key.

This confirmation bonus trading activity became so prominent that Alice stopped using the diary for her own purposes, and eventually all the records in the diary would only be about "who transferred which confirmation bonus to whom". This idea of a distributed proof-of-work-based blockchain with transferable confirmation bonuses is known as the Bitcoin.

Smart Contracts

But wait, we are not done yet. Note how Bitcoin is born from the idea of recording "transfer claims", cryptographically signed by the corresponding private key, into a blockchain-based journal. There is no reason we have to limit ourselves to this particular cryptographic protocol. For example, we could just as well make the following records:

This would be an example of a collective deposit, which may only be extracted by a pair of collaborating parties. We could generalize further and consider conditions of the form:

Here could be any predicate describing a "contract". For example, in Bitcoin the contract requires to be a valid signature, corresponding to a given public key (or several keys). It is thus a "contract", verifying the knowledge of a certain secret (the private key). However, could just as well be something like:

which would be a kind of a "future prediction" contract - it can only be evaluated in the future, once record 42000 becomes available. Alternatively, consider a "puzzle solving contract":

Finally, the first part of the contract, namely the phrase "Transfer bonus in record ..." could also be fairly arbitrary. Instead of transferring "bonuses" around we could just as well transfer arbitrary tokens of value:

The value and importance of such arbitrary tokens will, of course, be determined by how they are perceived by the community using the corresponding blockchain. It is not unreasonable to envision situations where being DA BOSS gives certain rights in the society, and having this fact recorded in an automatically-verifiable public record ledger makes it possible to include the this knowledge in various automated systems (e.g. consider a door lock which would only open to whoever is currently known as DA BOSS in the blockchain).

Honest Computing

As you see, we can use a distributed blockchain to keep journals, transfer "coins" and implement "smart contracts". These three applications are, however, all consequences of one general, core property. The participants of a distributed blockchain ("assistants" in the Alice example above, or "miners" in Bitcoin-speak) are motivated to precisely follow all rules necessary for confirming the blocks. If the rules say that a valid block is the one where all signatures and hashes are correct, the miners will make sure these indeed are. If the rules say that a valid block is the one where a contract function needs to be executed exactly as specified, the miners will make sure it is the case, etc. They all seek to get their confirmation bonuses, and they will only get them if they participate in building the longest honestly computed chain of blocks.

Because of that, we can envision blockchain designs where a "block confirmation" requires running arbitrary computational algorithms, provided by the users, and the greedy miners will still execute them exactly as stated. This general idea lies behind the Ethereum blockchain project.

There is just one place in the description provided above, where miners have some motivational freedom to not be perfectly honest. It is the decision about which records to include in the next block to be confirmed (or which algorithms to execute, if we consider the Ethereum blockchain). Nothing really prevents a miner to refuse to ever confirm a record "John is DA BOSS", ignoring it as if it never existed at all. This problem is overcome in modern blockchains by having users offer additional "tip money" reward for each record included in the confirmed block (or for every algorithmic step executed on the Ethereum blockchain). This aligns the motivation of the network towards maximizing the number of records included, making sure none is lost or ignored. Even if some miners had something against John being DA BOSS, there would probably be enough other participants who would not turn down the opportunity of getting an additional tip.

Consequently, the whole system is economically incentivised to follow the protocol, and the term "honest computing" seems appropriate to me.

Steganography is a marvelous subject, which could be considered a subfield of cryptography. Unfortunately, it is some-why absolutely underrated nowadays. It is not covered by the standard computer science curricula (although it would fit perfectly both within lectures on Cryptography as well as Signal Processing), and way too many people believe steganography is something akin to adding grey stamps to images in Photoshop. Even the almighty Wikipedia, in its corresponding article, does not provide a decently clear view of the field, in my opinion. To fix this I thought I'd give a try at making up a short explanation myself.

As mentioned, steganography is somewhat of a fellow discipline to cryptography. While the goal of cryptography is to protect the communication channel between Alice and Bob from some hypothetical evil Eve, the goal of steganography is to conceal the fact of communication itself. The classical setting is described as follows: Alice and Bob are kept imprisoned by the evil warden Walter. They are allowed to talk to each other, but Walter is listening to everything. How could Alice and Bob arrange a prison break without raising suspicion?

Steganographic problems

More specifically, steganographic problems can be divided into steganography against a passive warden, and steganography against an active warden.

Passive warden steganography

In this case Walter can only observe Alice and Bob's communication, but may not interfere. Walter's task is to be able to detect which of the messages between Alice and Bob contain secret meanings (if they do). If Walter comes up with a method by which he can distinguish innocent messages from the ones with a secret meaning with nontrivial probability, we shall say that Walter has succeeded in a "passive attack" on Alice and Bob's steganographic system.

Besides helping imaginary prisoners hide from imaginary wardens, passive steganography has many practical applications. For example, some printers add a barely visible watermark to each printed page, which identifies the printer model and the date. Radio and TV advertisers sometimes include in their clips a hidden identifier of the product being advertised (which simplifies automated airtime monitoring and validation). Storage of image metainfo within the image itself (e.g. storing the patient id within its X-ray picture) may prevent confusion when data is transferred or converted, etc.

It must be noted, that from the perspective of classical cryptography the methods mentioned above are not very interesting. Indeed, it is customary to assume in cryptography that all the details of the protocol used between Alice and Bob are open to all parties, including Walter. The only thing that Walter should not know is the "key". Without knowing this key Walter should be incapable of attacking the system. This is not the case in the examples with the printers and advertisements. No keys are involved and anyone who knows the algorithm can immediately discover the hidden message (i.e. attack the system).

The methods for designing such systems focus primarily on techniques for adding information to a known audio/video/textual signal without distorting it in a perceivable manner and, possibly, making the presence of this information resilient to transformations that the signal may pass (video streaming, file format conversion, text normalization, etc). Consequently, the complexity of many such methods lies mostly in the area of signal processing. In the case of audio, for example, it could mean finding sound frequency components that, on one hand, will be left unchanged by most audio codecs, yet on the other hand could be modified without the listener perceiving the change. In some sense it resembles a fight between the codec (which attempts to remove any redundant channels) and the steganographic system (which aims to make use of any redundancy remaining).

Active warden steganography

A more interesting situation is where Walter is not only listening in to Alice and Bob's communications, but may also actively interfere, removing any potential hidden meanings. The best example here is copyright protection. They say that movies, when shown in cinemas, would usually contain a steganographic watermark in their video signal, which identifies the particular movie theatre. The "warden" here is a movie pirate, who might know about the existence of the watermark, and would be interested in removing it (without corrupting the movie itself, of course). Consequently, the watermark must be included in a way, where Walter the pirate is incapable of removing it, even if he knew all the details of the watermarking algorithm (except for a secret key, of course). Besides movie watermarking, similar techniques could be used by other authors to "sign" their creations so that their authorship could later be established, when necessary.

Methods

Multiple methods exist for solving both the active and passive warden steganography. Not being able to list all of them, I will mention just the two core concepts, which I think are enough for an introductory overview.

LSB-steganography

The most well-known example of steganography - least-significant-bit (LSB) steganography - is applicable to analog data, such as music and images. The idea is that small changes in some values (pixels, frequency components) of an analog signal would not affect the perception of the signal in a notable way. For example, by tuning some pixels in an image one could transmit several bits of additional information. Of course, the choice of those pixels should be determined using a shared secret key, otherwise Walter could easily detect or remove the covert message.

The problem in the most naive version of this approach is that not every pixel in an image can be safely modified. For example, in regions filled with a single color any such change will be easy to spot. This can be overcome by only picking the pixels with enough variability in their neighborhood. Another weakness of the method is that the steganogram may be easy to remove by resizing or cropping the image. This can be prevented by hiding information in the spectral components rather than pixels - those are more resistant to the usual transformations. In fact, if we are dealing with a photograph or anything else that will be saved as a JPEG file, this approach would be quite nontrivial to break. The same ideas are used for steganographic processing of audio and video signals as well.

Equivalence-class steganography

Quite often Alice has a choice for multiple options for sending the same message. For example, when writing a text message to Bob, she can choose the phrasings. She can write "Hi" instead of "Hello", "Robert" instead of "Bob", punctuation can be used in multiple ways, and so on. When Alice is writing a novel, she is free to choose the names of the characters and places, chapter titles and even the order of events. Knowing the possible equivalence classes for the messages to be sent (e.g. words or sentences) as well as a common key, Alice may easily choose her words so that only Bob would be able to grasp whether there is a secret meaning and, if so, what it is.

A simple practical example of a coding algorithm is the following: Alice will code a single bit by each sentence of her text. For obtaining this bit, Bob will have to apply a hash function to the sentence plus the secret key and use the last bit of that hash. During coding Alice will simply have to choose words so that each sentence would correspond to a correct bit.

In its bare form the method is easy to attack - Walter may try to rephrase the text himself on transmission. This, in turn, can be overcome if Alice would hide the bits only into particularly chosen words or word sets (which can only be found by knowing the key), and do it using redundant coding (thus Walter would need to significantly alter the text if he wanted to be sure the message is removed). If Alice hides the message into the names of the characters of her novel, Walter may have no chances at all.

Methods like that are claimed to be used by large software companies to watermark their code (here, instead of choosing synonymous words a specific algorithm will be choosing synonymous bytecode instructions). This makes it possible to track the particular license which was used to leak a pirated version. Another example is geographic mapping software, which may use various equivalent ways of displaying a fractal shore in order to watermark the image.

As noted, other approaches and techniques exist (I did not find the space to properly mention public key steganography here, for example), yet I belive that LSB and EC-steganography largely illustrate the core ideas behind modern steganography in general as well as its possibilities and limitations. For those interested in the security proofs behind such techniques, this paper is a must read.

Research and engineering always go hand in hand. Their relationship is so tight that often people cease to see the difference. Indeed, both are development activities that bring along technical advances. Many researchers work in engineering companies, many engineers do what is essentially research, is there even a need to see the difference? Quite often there is. Let me highlight this difference.

Research (sometimes synonymous with "science") is, ideally, an experimental activity, which aims to explore some space of possibilities in order to hopefully come up with a certain "understanding" of what those possibilities are or how they should be used. Researchers primarily deliver written reports, summarizing their findings. There is absolutely no guarantee that those findings would be "interesting" or "useful" to any degree - indeed, a research project by definition starts off in a position of uncertainty. As a result, for practical, commercial or investment purposes, research is always a risky activity. It may take a long time, it will produce mostly text, and there is no guarantee that the results will be of use. The upside of this risk is, of course, the chance to stumble upon unique innovation, which may eventually bring considerable benefits. Later.

Engineering is a construction activity, where existing knowledge and tools are put together to deliver actual products. In order for this process to be successful, experimentation and uncertainty must be, ideally, brought down to a minimum. Thus, when compared to pure research, engineering projects are low risk endeavors, where the expected outputs are known in advance.

In simple terms - researchers answer questions whilst engineers build things, and by this definition those occupations are, obviously, very different. This difference is often apparent in material fields, such as construction or electronics, where the engineers can be distinguished from the researchers by the kind of tools they would mostly hold in their hands and the places they would spend their time the most. With computational fields this visual difference does not exist - both engineers and researchers spend most of their time behind a computer screen. The tools and approaches are still different, but you won't spot this unless you are in the field. I did not know the difference between Software Engineering and Computer Science until I had the chance to try both.

Things become even more confusing when data mining gets involved. The popularity of projects, which focus on building data-driven intelligent systems, is ever growing. As a result, more and more companies seem to be eager to embrace this magical world by hiring "data scientists" to do "data science" for them. The irony of the situation is that most of those companies are engineering businesses (e.g. software developer firms) and, as such, they would not (or at least should not) normally consider hiring anyone with the word "scientist" in the job title. Because scientists are not too famous for bringing stable income, engineers are.

The term "data science" is a vague one, but I think it is quite succinct in that it captures the exploratory aspect that is inherent in general-purpose data analysis, as well as the current state of the art in the field. Although there are some good high level tools for a wide range of "simple" machine learning tasks nowadays, as soon as you want to try something more exotic, you are often on your own, faced with uncertainty and the need to experiment before you can even try to "build" anything. For a typical engineering company such uncertainty is not a good thing to rely upon.

It does not mean that one cannot engineer data-driven systems nowadays, it means that in reality most of the companies, whether they know it or not, need a very particular kind of "data scientists". They need specialists with a good knowledge of simple reliable tools and are capable of applying them to various data formats. Those, who would perhaps avoid excessive experimentation in favor of simple, scalable, working solutions, even if those are somehow simplistic, suboptimal and do not employ custom-designed forty-layer convolutional networks with inception blocks, which require several months to debug and train. Those, who might not know much about concentration inequalities but would be fluent in data warehousing and streaming. There's actually a name for such people: "Data engineers".

There is nothing novel about the use of such terminology, yet I still regularly encounter way too much misunderstanding around this topic over and over again.

In particular, I would expect way more of the "Data engineering" curricula to appear at universities alongside the more or less standard "Data science" ones. The difference between the two would be slight, but notable - pretty much of the same order as the difference between our "Computer science" and "Software engineering" master's programmes, for example.

This is a repost of my quora answer to the question: In layman's terms, how does Naive Bayes work?

Suppose that you are a working as a security guard at the airport. Your task is to look at people who pass the security line and pick some of them as being worthy of a more detailed screening. Now, of course, telling whether a person is a potential criminal or not by just looking at him/her is hard, if at all possible, but you need to do something. You have been put there for some reason, after all.

One of the simplest ways to approach the problem, mentally, is the following. You assign a "risk value" for each person. At the beginning (when you don't have any information about the person at all) you set this value to zero.

Now you start studying various features of the person in front of you: is it a male or a female? Is it a kid? Is he behaving nervously? Is he carrying a big bag? Is he alone? Did the metal detector beep? Is he a foreigner? etc. For each of those features you know (subconsciously due to your presuppositions, or from actual statistics) the average increase or decrease in risk of the person being a criminal that it entails. For example, if you know that the proportion of males among criminals is the same as the proportion of males among non-criminals, observing that a person is male will not affect his risk value at all. If, however, there are more males among criminals (suppose the percentage is, say, 70%) than among decent people (where the proportion is around 50%), observing that a person in front of you is a male will increase the "risk level" by some amount (the value is log(70%/50%) ~ 0.3, to be precise). Then you see that a person is nervous. OK, you think, 90% of criminals are nervous, but only 50% of normal people are. This means that nervousness should entail a further risk increase (of log(0.9/0.5) ~ 0.6, to be technical again, so by now you have counted a total risk value of 0.9). Then you notice it is a kid. Wow, there is only 1% of kids among criminals, but around 10% among normal people. Therefore, the risk value change due to this observation will be negative (log(0.01/0.10) ~ -2.3, so your totals are around -1.4 by now).

You can continue this as long as you want, including more and more features, each of which will modify your total risk value by either increasing it (if you know this particular feature is more representative of a criminal) or decreasing (if the features is more representative of a decent person). When you are done collecting the features, all is left for you is to compare the result with some threshold level. Say, if the total risk value exceeds 10, you declare the person in front of you to be potentially dangerous and take it into a detailed screening.

The benefit of such an approach is that it is rather intuitive and simple to compute. The drawback is that it does not take the cross-play of features into account. It may very well be the case that while the feature "the person is a kid" on its own greatly reduces the risk value, and the feature "has a moustache" on its own has close to no effect, a combination of the two ("a kid with a moustache") would actually have to increase the risk by a lot. This would not happen when you simply add the separate feature contributions, as described above.

Anyone who has had to deal with scientific literature must have encountered Postscript (".ps") files. Although the popularity of this format is gradually fading behind the overwhelming use of PDFs, you can still find .ps documents on some major research paper repositores, such as arxiv.org or citeseerx. Most people who happen to produce those .ps or .eps documents, do it using auxiliary tools, most commonly while typesetting their papers in LaTeX, or while preparing images for those papers using a vector graphics editor (e.g. Inkscape). As a result, Postscript tends to be regarded by the majority of its users as some random intermediate file format, akin to any of the myriad of other vector graphics formats.

I find this situation unfortunate and unfair towards Postscript. After all, PS is not your ordinary vector graphics format. It is a fully-fledged Turing-complete programming language, that is well thought through and elegant in its own ways. If it were up to me, I would include a compulsory lecture on Postscript into any modern computer science curriculum. Let me briefly show you why.

Stack-based programming

Firstly, PostScript is perhaps the de-facto standard example of a proper purely stack-based language in the modern world. Other languages of this group are nowadays either dead, too simple, too niche, or not practical. Like any stack language, it looks a bit unusual, yet it is simple to reason about and its complete specification is decently short. Let me show you some examples:

2 2 add     % 2+2 (the two numbers are pushed to the stack,
            % then the add command pops them and replaces with
            % the resulting value 4)
/x 2 def                  % x := 2 (push symbol "x", push value 2,
                          %         pop them and create a definition)
/y x 2 add def            % y := x + 2 (you get the idea)
(Hello!) show             % print "Hello!"
x 0 gt {(Yes) show} if    % if (x > 0) print "Yes"

Adding in a couple of commands that specify font parameters and current position on the page, we may write a perfectly valid PS file that would perform arithmetic operations, e.g:

/Courier 10 selectfont   % Font we'll be using
72 720 moveto            % Move cursor to position (72pt, 720pt)
                         % (0, 0) is the lower-left corner
(Hello! 2+2=) show
2 2 add                  % Compute 2+2
( ) cvs                  % Convert the number to a string.
                         % (First we had to provide a 1-character
                         % string as a buffer to store the result)
show                     % Output "4"

Computer graphics

Postscript has all the basic facilities you'd expect from a programming language: numbers, strings, arrays, dictionaries, loops, conditionals, basic input/output. In addition, being primarily a 2D graphics language, it has all the standard graphics primitives. Here's a triangle, for example:

newpath           % Define a triangle
    72 720 moveto
    172 720 lineto
    72 620 lineto
closepath
gsave             % Save current path
10 setlinewidth   % Set stroke width
stroke            % Stroke (destroys current path)
grestore          % Restore saved path again
0.5 setgray       % Set fill color
fill              % Fill

Postscript natively supports the standard graphics transformation stack:

/triangle {       % Define a triangle of size 1 n the 0,0 frame
    newpath
        0 0 moveto
        1 0 lineto
        0 1 lineto
    closepath
    fill
} def

72 720 translate      % Move origin to 72, 720
gsave                 % Push current graphics transform
    -90 rotate        % Draw a rotated triangle
    72 72 scale       % .. with 1in dimensions
    triangle
grestore              % Restore back to non-scaled, non-rotated frame
gsave
    100 0 translate   % Second triangle will be next to the first one
    32 32 scale       % .. smaller than the first one
    triangle          % .. and not rotated
grestore

Here is the result of the code above:

Two triangles

The most common example of using a transformation stack is drawing fractals:

/triangle {
    newpath
        0 0 moveto
        100 0 lineto
        0 -100 lineto
    closepath
    fill
} def

/sierpinski {
    dup 0 gt
    {
        1 sub
        gsave 0.5 0.5 scale dup sierpinski grestore
        gsave 50 0 translate 0.5 0.5 scale dup sierpinski grestore
        gsave 0 -50 translate 0.5 0.5 scale sierpinski grestore
    }
    { pop triangle }
    ifelse
} def
72 720 translate  % Move origin to 72, 720
5 5 scale
5 sierpinski

Sierpinski triangle

With some more effort you can implement nonlinear dynamic system (Mandelbrot, Julia) fractals, IFS fractals, or even proper 3D raytracing in pure PostScript. Interestingly, some printers execute PostScript natively, which means all of those computations can happen directly on your printer. Moreover, it means that you can make a document that will make your printer print infinitely many pages. So far I could not find a printer that would work that way, though.

System access

Finally, it is important to note that PostScript has (usually read-only) access to the information on your system. This makes it possible to create documents, the content of which depends on the user that opens it or machine where they are opened or printed. For example, the document below will print "Hello, %username", where %username is your system username:

/Courier 10 selectfont
72 720 moveto
(Hi, ) show
(LOGNAME) getenv {} {(USERNAME) getenv pop} ifelse show
(!) show

I am sure, for most people, downloading a research paper from arxiv.org that would greet them by name, would probably seem creepy. Hence this is probably not the kind of functionality one would exploit with good intentions. Indeed, Dominique has an awesome paper that proposes a way in which paper reviewers could possibly be deanonymized by including user-specific typos in the document. Check out the demo with the source code.

I guess this is, among other things, one of the reasons we are going to see less and less of Postscript files around. But none the less, this language is worth checking out, even if only once.

Playing cards are a great tool for modeling, popularizing and explaining various mathematical and algorithmic notions. Indeed, a deck of cards is a straightforward example for a finite set, a discrete distribution or a character string. Shuffling and dealing cards represents random sampling operations. A card hand denotes information possessed by a party. Turning card face down or face up looks a lot like bit flipping. Finally, card game rules describe an instance of a particular algorithm or a protocol. I am pretty sure that for most concepts in maths or computer science you can find some card game or a card trick that is directly related to it. Here are some examples of how you can simulate a simple computing machine, illustrate inductive reasoning or explain map-reduce, in particular.

Cryptographers seem to be especially keen towards playing cards. Some cryptographic primitives could have been inspired by them. There are decently secure ciphers built upon a deck of cards. Finally, there are a couple of very enlightening card-based illustrations of such nontrivial cryptographic concepts as zero-knowledge proofs and voting protocols. The recent course on secure two-party computation given by abhi shelat at the last week's EWSCS extended my personal collection of such illustrations with another awesome example — a secure two-party protocol for computing the AND function. As I could not find a description of this protocol anywhere in the internet (and abhi did not know who is the author), I thought it was worth being written up in a blog post here (along with a small modification of my own).

The Tinder Game

Consider the situation, where Alice and Bob want to find out, whether they are both interested in each other (just as if they were both users of the Tinder app). More formally, suppose that Alice has her private opinion about Bob represented as a single bit (where "0" means "not interested" and "1" means "interested"). Equivalently, Bob has his private opinion about Alice represented in the same way. They need to find out whether both bits are "1". However, if it is not the case, they would like to keep their opinions private. For example, if Alice is not interested in Bob, Bob would prefer Alice not to know that he is all over her. Because, you know, opinion asymmetry may lead to awkward social dynamics when disclosed, at least among college students.

The following simple card game happens to solve their problem. Take five cards, so that three of them are red and two are black. The cards of one color must be indistinguishable from each other (e.g. you can't simply take three different diamonds for the reds). Deal one black and one red card to Alice, one black and one red card to Bob. Put the remaining red card on the table face up.

Initial table configuration

Now Alice will put her two cards face down to the left of the open card, and Bob will put his two cards to the right of the open card:

Alice and Bob played

The rules for Alice and Bob are simple: if you like the other person, put your red card next to the central red card. Otherwise, put your black card next to the central one. For example, if both Alice and Bob like each other, they would play their cards as follows (albeit still face down):

What Alice and Bob would play if they both liked each other

Now the middle card is also turned face down, and all five cards are collected, preserving their order:

Five cards collected, preserving order

Next, Alice cuts this five-card deck, moving some number of cards from the top to the bottom (Bob should not know exactly how many). Then Bob cuts the deck (also making sure that Alice does not know how many cards he cuts). The result is equivalent to applying some cyclic rotation to the five card sequence yet neither Bob nor Alice knows how many cards were shifted in total.

The five cards can now be opened by dealing them in order onto the table to find out the result. If there happen to be three red cards one after another in a row or two black cards one after another, Alice and Bob both voted "yes". Here is one example of such a situation. It is easy to see that it is a cyclic shift of the configuration with three red aces in the middle shown above.

Both voted "yes"

Otherwise, if neither three red aces nor two black aces are side by side, we may conclude that one or both of the players voted "no". However, there is absolutely no way to find out anything more specific than that. Here is an example:

No mutual affection (or no affection at all)

Obviously, this result could not be obtained as a cyclic shift of the configuration with three aces clumped together. On the other hand, it could have been obtained as a cyclic shift from any of the three other alternatives ("yes-no", "no-no" and "no-yes"), hence if Alice voted "no" she will have no way of figuring out what was Bob's vote. Thus, playing cards along with a cryptographic mindset helped Alice and Bob discover their mutual affection or the lack of it without the risk of awkward situations. Isn't it great?

Throwing in a Zero-Knowledge Proof

There are various ways Alice or Bob can try to "break" this protocol while still trying to claim honesty. One possible example is shown below:

Alice is trying to cheat

Do you see what happened? Alice has put her ace upside down, which will later allow her to understand what was Bob's move (yet she can easily pretend that turning a card upside down was an honest mistake). Although the problem is easily solved by picking a deck with asymmetric backs, for the sake of example, let us assume that such a solution is somewhy unsuitable. Perhaps there are no requisite decks at Alice and Bob's disposal, or they need to have symmetric backs for some other reasons. This offers a nice possibility for us to practice even more playing card cryptography and try to secure the original algorithm from such "attacks" using a small imitation of a zero-knowledge proof for turn correctness.

Try solving it yourself before proceeding.

Read more...