Four Years Remaining

Whenever you write a program, you want this program to behave correctly and do what you want it to do. Thus, programming always goes together with the mental act of proving to yourself (and sometimes to other people as well), that the code you write is correct. Most often this "proof" is implicit, dissolved in the way you write your code and comment it. In fact, in my personal opinion, "good code" is exactly the one, where a human-reviewer is able to verify its correctness without too much effort.

It is natural to use computers to help us verify correctness. Everyone who has ever programmed in a strictly-typed programming language, such as Java or Haskell, is familiar with the need to specify types of variables and functions and follow strict rules of type-safety. But of course, ensuring type-safety is just the compiler's way to help you ensure some basic claims about the program, such as "this variable will always contain an integer" or "this function will always be invoked with exactly three parameters".

This is very convenient, yet can be somewhat limiting or annoying at times. After all, type-safety requires you to write code that "can be type-checked". Although very often this is expected of "good code" anyway, there are situations where you would like some more flexibility. For this reason some languages impose no type-safety rules at all (e.g. Python or Javascript), and some languages let you disable type-checking for parts of code.

Rather than disabling the type checker, another principled way to allow more flexibility is to make the type-checker smarter. This is the promise of dependent types. In principle, a language, which supports dependent types, would let you make much more detailed statements about your program and have your program automatically checked for correctness with respect to those statements. Rather than being limited to primitive claims like "this variable is an integer", the use of dependent types enables you to assert things like "this is a sorted list", or "this is an odd integer", and so on up to nearly arbitrary level of detail, in the form of a type annotation. At least that much I found out during a course at the recent winter school.

The course was based on the Agda programming language, and the first thing I decided to try implementing in Agda is a well-typed version of the following simple function:

f t = if t then true else 0

It might look like something trivial, yet most traditional strictly typed languages would not let you write this. After all, a function has to have a return type, and it has to be either a Boolean or an Integer, but not both. In this case, however, we expect our function to have a parameter-dependent type:

f : (t : Bool) → if t then Bool else Integer

Given that Agda is designed to support dependent types, how complicated could it be to implement such a simple function? It turns out, it takes a beginner more than an hour of thinking and a couple of consultations with the specialists in the field. The resulting code will include at least three different definitions of "if-then-else" statements and, I must admit, some aspects of it are still not completely clear to me.

IF-THEN-ELSE in Agda, including all the boilerplate code

This is the longest code I've ever had to write to specify a simple if-then-else statement. The point of this blog post is to share the amusement and suggest you to check out Agda if you are in the mood for some puzzle-solving.

As for dependent types, I guess those are not becoming mainstream any time soon.

CrapCon is a fun evening session, which traditionally takes place at the annual Estonian Winter School on Computer Science (EWSCS), where participants of EWSCS are welcome to make short random nonsensical talks, prepared earlier on the same day during the lectures.

The following is my presentation from this year's CrapCon. The first part of it, as is customary for most CrapCon talks, makes fun of the topics being taught during the school, hence it might not make much sense outside the context of the event. The second part is fairly general (and totally serious!), though.

If you find that amusing, certainly check out the talk by Taivo Lints, which is, I think, among the best examples of computer-science-related abstract humor.

This relates nicely to several previous posts here.

Copyright © xkcd.

For many people, the ability for learning and adaptation seems like something unique, extremely complicated and mysterious. Indeed, those are the abilities we almost exclusively associate with high levels of intelligence and knowledge. This is, however, an illusion. Although adaptive behaviour might indeed look complex, it is not necessarily driven by "intelligent" mechanisms. One of the best illustrations of this is a fully-fledged self-learning machine made from plain matchboxes.

A Tic-Tac-Toe machine by James Bridle

The idea for such a machine was first introduced in 1960 by Donald Michie, who devised a simple self-learning algorithm for Tic-Tac-Toe (reminiscent of what is now known to be Reinforcement Learning). Due to lack of appropriate computing power, he implemented it "in hardware" using 300 or so matchboxes.

The idea of the machine is simple. There is a matchbox corresponding to each game position, where the "computer" has to make a move. The matchbox contains colored beads, each color corresponding to a particular move. The decision is made by picking a random bead from the matchbox. Initially (when the machine is "untrained"), there is an equal number of beads of each color, and the machine thus makes equiprobably random turns. After each game, however, the machine is "punished" by removing beads, corresponding to losing turns, or "rewarded" by adding beads, corresponding to winning turns. Thus, after several games, the machine will adapt its strategy towards a winning one.

The idea was popularized by Martin Gardner in one of his Scientific American articles (later published in the book "The Unexpected Hanging and Other Mathematical Diversions"). Gardner invented a simple game of  "Hexapawn", and derived a matchbox machine for it, which only required as little as 19 matchboxes. He also suggests in his article, however, to create a matchbox machine for "Mini-checkers" - checkers played on a 4x4 board. Ever since I saw this article some 20 or so years ago I was thinking of making one. This summer, while teaching a machine learning course in a summer school in Kiev, I actually made one. I could use it to both fulfil my ages-old desire as well as a teaching aid. You can make one too now, if you are interested.

The Mini-checkers Machine

The rules of mini-checkers are exactly like those of usual checkers, with three modifications:

• The game is played on a 4x4 field. White is the first one to move. Machine plays for black.
• Whenever both players get a King, the game immediately ends in a draw.
• The King must always move to the furthest possible position in the chosen direction.

To make the machine, you first have to buy and empty 24 matchboxes. Next, print out and stick the 24 game positions onto the boxes. Draw on each box all the possible black's moves as arrows using colored markers. Finally, for  each colored arrow, add 2 beads of the same color into the matchbox. That's it, your machine is ready to play.

The Mini-checkers machine

The game proceeds as already described: whenever the machine (the black player) has to make a decision (i.e. whenever it has to make a move and there is more than one possibility), find the matchbox with the current position depicted on it, shake it, and pick a random bead. This will tell you the decision of the machine. If the corresponding matchbox is empty, the machine forfeits. You should keep the matchboxes, corresponding to the moves that were made, open until the end of the game.

Once the game is over, the machine is "taught":

• If the machine won, do nothing.
• If the game was a draw, remove the bead corresponding to the machine's last move from the matchbox, unless it was the last bead of that color in the box.
• If the machine lost, remove all the beads, corresponding to the machine's last move, from the last matchbox.

It takes about 30 games or so for the machine to actually learn to play well enough. Of course, a human would understand the strategy much earlier, but it's fun none the less.

Playing with the machine will immediately lead you towards two important questions:

• How efficient is the suggested learning procedure? Can it be improved and generalized?
• How do you make a matchbox machine for a more complex game without having to manage thousands of matchboxes.

As far as I know, contemporary machine learning has only partial answers to both of them.

This post presumes you are familiar with PCA.

Consider the following experiment. First we generate a random vector (signal) as a sequence of random 5-element repeats. That is, something like

(0.5, 0.5, 0.5, 0.5, 0.5,   0.9, 0.9, 0,9, 0.9, 0,9,   0.2, 0.2, 0.2, 0.2, 0.2,   ... etc ... )

In R we could generate it like that:

num_steps = 50
step_length = 5;
initial_vector = c();
for (i in 1:num_steps) {
  initial_vector = c(initial_vector, rep(runif(1), step_length));
}

Here's a visual depiction of a possible resulting vector:

plot(initial_vector), zoomed in

Next, we shall create a dataset, where each element will be a randomly shifted copy of this vector:

library(magic) # Necessary for the shift() function
dataset = c()
for (i in 1:1000) {
  shift_by = floor(runif(1)*num_steps*step_length) # Pick a random shift
  new_instance = shift(initial_vector, shift_by)   # Generate a shifted instance
  dataset = rbind(dataset, new_instance);          # Append to data
}

Finally, let's apply Principal Component Analysis to this dataset:

pca = prcomp(dataset)

Question - how do the top principal components look like? Guess first, then read below for the correct answer.

Read more...

It is not uncommon when a long-running scientific study or an experiment produces results which are, at best, uninteresting. The measured effect may be too weak to be reported on convincingly given the data at hand. None the less, resources have been put into it, many man-months have been spent, and thus a paper must be published. The researcher must therefore present his results in a way convincing enough for the reviewers to be lulled into acceptance.

The following are the three best methods for doing that (and I have seen those being used in practice). Next time you read someone's paper (or write your own), keep them in mind.

1. Use an irrelevant (and preferably strict) hypothesis test.
   Suppose you want to show that a set of measurements in one group differs from the set of measurements in the other group. The typical approach here is the T-test or the Wilcoxon test, both of which detect whether elements in one group are on average greater than those in the other group. If, however, you find that the tests fail on your data (i.e., there is no easily detectable difference in measurement magnitudes), why don't you try something like the Kolmogorov-Smirnov test, which checks whether the distributions of the two groups are different. It is a much stricter condition. In fact the tiniest outlier in your data will easily get you a low p-value and thus something to stick in the face of a reviewer. If even the KS test did not work, try testing something even less relevant, such as, whether your data is normally distributed. Most probably it is not, here's your low p-value! Remember - the smaller your p-values, the better is your paper!
2. Avoid significance testing completely
   If you can't get a low p-value anywhere, do not worry. Significance testing is going somewhat out of fashion nowadays anyway, so it is possible to avoid it and still sound convincing. If one group of measurements has 40% of successes and the other has 42% - why not simply present those two numbers as obvious proof that the second group is better. Using ratios is also a smart idea. Say, some baseline algorithm has a 1% chance of success. You now test your algorithm and discover that out of 10 trials it had 1 success. That means your algorithm has just demonstrated a 10% success rate, which is ten times better than the baseline! Finally, ROC curves can often be used to hide the fact that your data is too tiny to make any conclusions. No one really ever checks for significance of those.
3. Sweep multiple testing under the carpet
   If you are analyzing a dataset with 1000 attributes and 50 datapoints, it is not really very surprising if one of those attributes will seem "interesting" (e.g. highly correlated with the target effect) purely by chance - there is often nothing significant in finding one out of a thousand. However, if you only mention that one (or perhaps 10-50) of the original attributes, your results will magically become significant and no reviewer will be able to catch your cheating.

There are certainly more, and I'll keep the post updated if I come up with a worthy addition. If you have something to add, please do comment.

I do not know who is the author, but I think this is great:

This year I have been lucky to be taking part in the Robotex robot-building course. Despite being an awful time-sink, it is also uniquely enlightening. Our team has a blog, documenting the progress. If you think you might be interested to see what does "making a small robot" mean, and what kind of problems may come on the way, do take a peek:

http://robotex.ing.ee/

I have recently realized that my HP 8440p laptop has a built-in "Qualcomm un2420 Broadband Module" device, also known as a "3G modem". For some reason no drivers were preinstalled for it on my system, and with the SIM card slot concealed behind the battery, it was not something I noticed immediately. Once the drivers were installed, the operating system had no problem recognizing the new "Mobile Broadband Connection" opportunity, and with the SIM card in the slot, I could connect to the Internet via 3G, yay.

Knowing that there is more to mobile communication than Internet access, I was wondering whether I could do anything else, like voice calls or SMS. Unfortunately, my attempts of finding any reasonable software packages, which would open up the power of 3G to me at the click of a button, failed. Instead, however, I discovered that it is actually quite easy to communicate with the modem directly. It turns out you can control your shiny bleeding-edge 3.5G device by sending plain old AT commands to it over a serial port. This is the same protocol that the wired grandpa-modems have been speaking since the 70s and it is fun to see this language was kept along all the way into the wireless century.

Let me show you how it works. Try to follow along — this is kinda fun.

Finding your Modem

If your computer does not have a built-in 3G modem, chances are high your garden variety cellphone does (not to mention smartphones, of course). If it is the case, then:

• Switch on the Bluetooth receiver on your phone (for older Nokias this is usually in the "Settings -> Connectivity -> Bluetooth" menu).
• On your computer, go to "Devices and Printers", click "Add a device", wait until your phone appears on the list, double click it and follow the instructions to establish the connection. (I'm talking about Windows 7 here, but the procedure should be similar for most modern OSs).
• Once the computer recognizes your phone and installs the necessary drivers, it will appear as an icon in the "Devices" window. Double click it to open the "Properties" window, and make sure there is a "Standard Modem over Bluetooth link" function or something similar in the list.
  

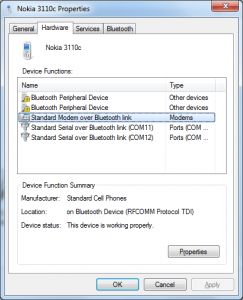
  Cellphone Functions

• Double-click that "modem" entry, a new properties window opens. Browse along in it, and find the COM port number that was assigned to the modem.
  

  Bluetooth modem at port COM9

If you do have a 3G modem bundled with your laptop (and you have the drivers installed), open the Device manager ("Control Panel -> Device Manager"), find the modem in the list, double click to open the "Properties" page, and browse to the "Modem" tab to find the COM port number.

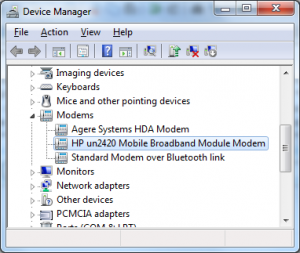
Laptop 3G modem in Device Manager

Connecting to the Modem

Next thing - connect to the COM port. In Windows use PuTTY to do it. In Linux use minicom. Don't worry about the settings — the defaults should do.

PuTTY connection dialog

Once the connection starts, you will get a blank screen with nothing but a cursor. Try typing "AT+CGMI" followed by a <RETURN>. Note that, depending on the settings of your device and the terminal program, you might not see your letters being typed. If so, you will have to reconfigure the terminal (enable "local echo"). But for now, just type the command. You should get the name of the manufacturer in response. You can also get the word "ERROR" instead. This means that your modem is ready to talk to you, but it either does not support the "AT+CGMI" command OR requires you to enter the PIN code first. We'll get to it in a second. If you get no response at all, you must have connected to the wrong COM port.

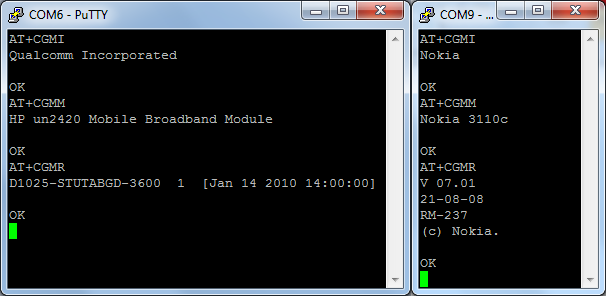
Terminal sessions with a Qualcomm (left) and Nokia (right) 3G modems

You can get more information about the device using the "AT+CGMM", "AT+CGMR", "AT+CGSN" commands. Try those.

Authentication

To do anything useful, you need to authenticate yourself by entering the PIN (if you use your cellphone over bluetooth, you most probably already entered it and no additional authentication is needed). You can check whether you need to enter PIN by using the command "AT+CPIN?" (note the question mark). If the response is "+CPIN: READY", your SIM card is already unlocked. Otherwise the response will probably be "+CPIN: SIM PIN", indicating that a PIN is expected to unlock the card. You enter the pin using the "AT+CPIN=<your pin>" command. Please note, that if you enter incorrect PIN three times, YOUR SIM CARD WILL BE BLOCKED (and you will have to go fetch your PUK code to unblock it), so be careful here.

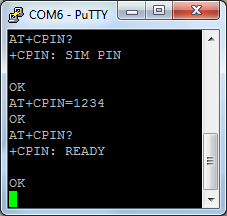
Entering the PIN

Doing Stuff

Now the fun starts: you can try dialing, sending and receiving messages and do whatever the device lets you do. The (nonexhaustive) list of most interesting commands is available here. Not all of them will be supported by your device, though. For example, I found out that the laptop's 3G modem won't let me dial numbers, whilst this was not a problem for a cellphone connected over bluetooth (try the command "ATD<your number>;" (e.g. "ATD5550010;")). On the other hand, the 3G modem lets me list received messages using the "AT+CMGL" command, while the phone refused to do it.

One useful command to know about is "AT+CUSD", which lets you send USSD messages (those "*1337#" codes) to the mobile service provider. For example, the prepaid SIM card I bought for my computer allows to buy a "daily internet ticket" (unlimited high-speed internet for 12 hours for 1 euro) via the "*135*78#" code. Here's how this can be done via terminal.

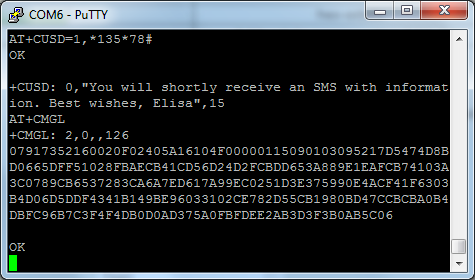
Sending an USSD code and receiving an SMS

We first send "AT+CUSD=1,*135*78#" command, which is equivalent to dialing "*135*78#" on the phone. The modem immediately shows us the operator's response ("You will shortly receive an SMS with information..."). We then list new SMS messages using the "AT+CMGL" command. There is one message, which is presented to us in the PDU encoding. A short visit to the online PDU decoder lets us decrypt the message - it simply says that the ticket is activated. Nice.

Sending an SMS

Finally, here's how you can send a "flash" SMS (i.e. the one which does not get saved at the receiver's phone by default and can thus easily confuse people. Try sending one of those at night - good fun). We start with an ATZ to reset the modem, just in case. Then we set message format to "text mode" using the "AT+CMGF=1" command (the alternative default is the "PDU mode", in which we would have to type SMS messages encoded in PDU). Then we set message parameters using the "AT+CSMP" command (the last 16 is responsible for the message being 'flash'). Finally, we start sending the message using the "AT+CMGS=<phone number>" command. We finish typing the message using <Ctrl+Z> and off it goes.

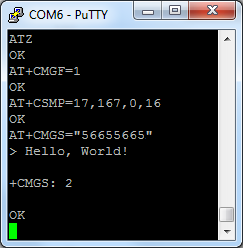
Sending a "Flash" SMS

For more details, refer to this tutorial or the corresponding specifications.

All in all, it should be fairly easy to make a simple end-user interface for operating the 3G modem, it is strange that there is not much free software available which could provide this functionality. If you find one or decide to make one yourself, tell me.

The Riddle

After the lecture on supervised machine learning at the University of Mordor, the teacher, Sauron, gave the students a dataset of the following form:

            1) ABACDAFXYZ    -> good
            2) CEGXEAELWMN   -> good
            3) NUWAB         -> bad
                    ...
           20) QRELAZMNPCXA  -> good

The inputs were seemingly arbitrary strings of latin characters: these were the terrible spells known only to Sauron and chosen by Sauron at random from his Great Book of Terrible Spells. The output was a binary variable, classifying each spell as good or bad. There were 20 observations in total in the dataset.

The students were given a task: on the basis of this data, come up with a generic spell classifier. Sauron promised to test their result on the next lecture as follows: he will pick another random terrible spell from the book and require each student to make a prediction. The student whose prediction is wrong will have to jump down from the tower as a punishment.

The first student, Aghargh, who happened to be slacking on the lecture, couldn't come up with any smart ways to solve the task, so he ended up just counting the proportion of "good" and "bad" spells in the dataset. Having observed that 16 of the 20 spells were "good", he decided to predict "good" when asked.

The second student, Bughrorc, chose a smarter way. Firstly, he converted each string into a vector of binary attributes — one attribute for each letter, having value "1" if that letter was present in the corresponding spell and "0" otherwise. He then split the data randomly into a training set (15 instances) and a test set (5 instances), and attempted training various classifiers using the MordorMiner software. After some experimenting he finally found five classifiers that could predict all of the training examples correctly. One of these also predicted all of the testing examples correctly. He decided to use this classifier on the forthcoming test.

On the day of testing, Sauron asked the students to classify the spell YOZAZA. Aghargh, as he decided, provided the answer "good". Bughrorc's classifier analyzed the string and claimed that the answer should be "bad"

Which of the students, do you think, might have a better chance of not jumping from the tower? Why? Can you quantify your answer?